Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Newton's Second Law and Acceleration
Unlock Audio Lesson
Today, we'll explore Newton's second law, which states that force is equal to mass times acceleration. Imagine you're pushing a fluid particle; how does its mass affect its acceleration?
So, if the mass is higher, the acceleration would be lower if the same force is applied, right?
Exactly! Now, let's connect this to fluid dynamics. At the particle level, acceleration is crucial because it's defined as the time derivative of velocity.
What do you mean by time derivative of velocity?
Great question! It simply means how quickly velocity is changing over time.
Can you give an example of that?
If a particle speeds up, its velocity increases, and thus, its acceleration becomes positive. If it slows down, that would be negative acceleration.
So, acceleration tells us about the speed of the particle's change?
That's correct! Acceleration essentially describes the rate of change of velocity. Let's summarize this part: acceleration is the change in velocity over time, and it's related to force through mass, according to Newton's second law.
Understanding Local and Convective Acceleration
Unlock Audio Lesson
Now, let's talk about the two types of acceleration: local and convective. Student 1, can you explain what local acceleration is?
Isn't local acceleration the change in velocity just at a specific point in time?
Exactly! It represents how a particle's velocity changes at a fixed position with respect to time. On the other hand, Student 2, what do you think convective acceleration is?
Is that related to how the velocity changes because the particle is moving through a varying field?
Spot on! Convective acceleration occurs when a particle moves into areas of differing velocities. Hence, velocity changes due to the fluid's spatial velocity field. This forms the basis for understanding complex fluid flows.
So, both depend on how the particle behaves — one is just looking locally, and the other looks at how it interacts with its environment?
Exactly! In summary, local acceleration is about instantaneous change in velocity, while convective acceleration focuses on changes due to spatial movement in the fluid flow.
Taylor Series and Multi-dimensional Analysis
Unlock Audio Lesson
Now let's delve into the Taylor series expansion, which helps us understand behavior in multi-dimensional space. Who can remind me what the Taylor series does?
It helps to approximate functions using derivatives!
Well said! In our case, we can use it to expand velocity in terms of x, y, z, and time. Can anyone give an example of how we could apply it?
We can look at the velocity at a point and see how it changes around that point in these directions?
That's correct! This approach provides insights into fluid behavior around a given point by analyzing how velocities change with respect to their position in space and time. In summary, Taylor series can model the variations of velocity in fluids effectively across multiple dimensions.
Eulerian vs. Lagrangian Framework
Unlock Audio Lesson
Let's now differentiate between the Eulerian and Lagrangian perspectives in fluid dynamics. Student 3, can you share what Eulerian entails?
That's when you focus on specific points in space and observe fluid properties over time, right?
Exactly! And now, Student 1, what about the Lagrangian approach?
It involves following individual particles through their paths as they move, analyzing how their properties change.
Correct! Both perspectives provide unique insights: Eulerian focuses on flow patterns at fixed locations, while Lagrangian tracks particle trajectories. It's important to use these frameworks to fully understand fluid dynamics.
I see! So it's like looking at a game from two different angles — one from the field and one from the players?
That's a perfect analogy! In summary, Eulerian observes field points while Lagrangian tracks particle movement, providing a comprehensive understanding of fluid behavior.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The chapter explores Newton's second law of motion at the particle level, describing how acceleration can be defined as the time derivative of velocity. It explains the local and convective components of acceleration, highlighting the significance of the Taylor series in understanding these concepts.
Detailed
Detailed Summary
This section focuses on the foundational concepts of particle mechanics in fluid dynamics, particularly how acceleration is defined as the time derivative of velocity at the particle level. The relationship between force, mass, and acceleration is re-established through Newton's second law, denoting force as a vector component represented as mass multiplied by acceleration.
When considering fluid particles, the acceleration can be computed as the local change in velocity over time. This demand leads to a necessary understanding of variations in position and time, which requires a breakdown of acceleration into two primary components: local and convective.
- Local Acceleration: This component represents the acceleration depending solely on the change of velocity with respect to time at a specific location.
- Convective Acceleration: This arises due to spatial variations in velocity, highlighting how different parts of the fluid may experience different accelerations due to the fluid's movement through space.
The Taylor series further provides a mathematical framework to expand these definitions across multiple dimensions, indicating that velocity can vary based on the x, y, and z coordinates and time. This is essential when formulating the behavior of particle velocities and their respective accelerations in three-dimensional space.
Furthermore, the significance of Eulerian and Lagrangian frames of reference is explored, linking the observed effects of fluid dynamics on both individual particles and the overall flow characteristics. The section concludes with the introduction of the material derivative, which reflects how quantities change along the path of fluid particles, encapsulating concepts of local and convective acceleration in a unified formalism.
Youtube Videos
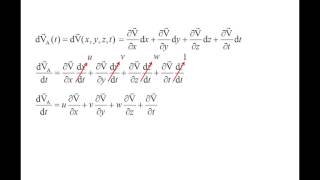
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Acceleration at Particle Levels
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let us look it at the particle levels, if I had to find out what is the acceleration of the fluid particles? Is nothing else is a time derivative of velocity of the particles, as you know it from class 10, 11th and 12th I am just doing this time derivative of the velocity; particle velocities with respect to time and that is what represents the accelerations, at the particles levels you will have these.
Detailed Explanation
Acceleration is defined as the rate of change of velocity over time. When considering fluid particles, the acceleration can be determined by taking the time derivative of the particle's velocity. In simpler terms, if you know how the velocity of a particle changes as time passes, you can calculate the acceleration. This is similar to how you might have learned in previous classes about the concept of acceleration in physics.
Examples & Analogies
Think of a car going from rest to speeding up. When you press the accelerator, the speed of the car increases. If you measure how fast your speed is changing at different moments (like 5 seconds, 10 seconds, etc.), that tells you how much you're accelerating. The same principle applies to fluid particles in motion.
Factors Affecting Velocity Variability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if you look at this the velocities has a variability in a positions and the time because of that though when you define a; derivative with respect to time you will have a local component okay, you will have a with a x particle directions, y particle directions and z particle direction.
Detailed Explanation
The velocity of fluid particles can change based on their position in space (x, y, z coordinates) and over time. This means that when calculating acceleration, you need to consider how the velocity changes in different directions (left-right, up-down, forward-backward) and how it can vary with respect to time. Thus, when defining derivatives, you often break it down into components along these different axes.
Examples & Analogies
Imagine a river. The flow speed might change in different parts of the river due to various factors like rocks or bends. If you were to measure how fast the water at one point flows compared to another point, you are essentially observing velocity variability based on position. This is similar to how we analyze changes in velocity for fluid particles.
Taylor Series Expansion in Multiple Variables
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is nothing else if you are considering is a 2 variables like I just discussed you the Taylor series, if you remember it defining for the 2 variables in this case, I have a Taylor series of 4 variables the x, y, z and the t.
Detailed Explanation
In mathematics, a Taylor series can be used to approximate functions. When dealing with fluid dynamics, you can extend this idea to account for multidimensional changes, such as in x, y, z coordinates and time (t). A Taylor series expansion allows us to express data (like velocity) in terms of derivatives at a single point, helping to analyze how these variables interact.
Examples & Analogies
Consider a balloon being inflated (where changes occur in all directions). If you want to predict how the balloon's size changes with time based on how you inflate it at different rates, you can think of extending that logic using a Taylor series for your calculations—meaning that knowing how one part affects another can inform you about the whole balloon.
Local and Convective Acceleration Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, this is 2 components; one is local acceleration component and other is convective acceleration. In vector (()) (45:37), we can very simple way represented the local accelerations and the convective acceleration component.
Detailed Explanation
Local acceleration refers to how the velocity of a fluid particle changes at a specific point in time and space, whereas convective acceleration takes into account the change in velocity due to the motion of the fluid particles themselves. In simple terms, local acceleration is about how fast the flow is changing in one location, and convective acceleration is about how flow properties change as you track the movement of the particles over space.
Examples & Analogies
Imagine riding a wave in the ocean. As you move with the wave (convective acceleration), you are also noticing how the water around you changes in speed (local acceleration). These two effects work together to give you a complete picture of your experience in the wave's motion.
Material Derivative Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But many of the times people talk about material derivative, it is nothing else, it is that the change it is a special name of material derivative means, when you talk about a particles along the particles, you compute the derivative with respect to time is a total derivative or the material derivative or the particle derivatives is nothing else, we already proved it that these derivatives we can define as these functions that is what we have defined it, okay.
Detailed Explanation
The material derivative is a way to describe how a fluid particle's properties change as it moves through space and time. It's an important concept in fluid mechanics because it combines the effects of local and convective changes. In simpler terms, it helps us understand the changes experienced by a fluid particle as it flows along.
Examples & Analogies
Think of a floating leaf on a river. The material derivative would help describe how the leaf’s position and speed change as it travels down the river (convective changes), as well as any other changes it experiences (like the water having different speeds at different locations).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Newton's Second Law: States that force equals mass times acceleration, foundational to understanding motion in fluids.
-
Acceleration: Rate of change of velocity of fluid particles in a time-dependent manner.
-
Local Acceleration: Change in velocity at a specific point over time.
-
Convective Acceleration: Change in velocity experienced by particles moving through a space of varying velocities.
-
Taylor Series: A mathematical tool to expand and analyze functions in multiple dimensions.
-
Eulerian Framework: Observes fluid characteristics from a fixed spatial point.
-
Lagrangian Framework: Tracks particles and their properties as they move through space.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of local acceleration: If a fluid particle at a given point has its velocity increase from 1 m/s to 3 m/s over 2 seconds, the local acceleration can be calculated as (3-1)/2 = 1 m/s².
-
For convective acceleration, consider a particle moving through a velocity field where the speed decreases as it travels further along its path, leading to an observed acceleration as a function of the particle's trajectory.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When speed goes up, you can lump, the force must push; don’t just slump!
📖 Fascinating Stories
-
Imagine a racecar on a track: as it speeds up due to the force of the engine, its acceleration increases, illustrating Newton’s second law in action. The racecar experiences local acceleration as it speeds up at a specific point on the track, and convective acceleration as it enters a straight, faster part of the track.
🧠 Other Memory Gems
-
F=ma means that Force is mass times acceleration: F(MA). Remember, for Local, think of a Fixed Spot; for Convective, think about how particles move through varying spaces.
🎯 Super Acronyms
L.A.C. for Local Acceleration is Changeable, C.A.C. for Convective Acceleration is Contextual.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Acceleration
Definition:
The rate of change of velocity of a particle over time.
-
Term: Local Acceleration
Definition:
The component of acceleration that represents the change in velocity at a specific point in time and location.
-
Term: Convective Acceleration
Definition:
Acceleration that occurs due to spatial variations in fluid velocity as a particle moves through different areas.
-
Term: Newton's Second Law
Definition:
A fundamental principle of motion stating that force equals mass times acceleration (F=ma).
-
Term: Taylor Series
Definition:
A mathematical series used to approximate functions by considering derivatives at a single point regarding multiple variables.
-
Term: Eulerian Framework
Definition:
A perspective in fluid dynamics that observes properties of the fluid at fixed points in space.
-
Term: Lagrangian Framework
Definition:
A perspective in fluid dynamics that follows individual particles and their properties as they move through space.