Convective Acceleration
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Convective Acceleration
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will explore convective acceleration, an important concept in fluid dynamics. Can anyone tell me how acceleration might be defined in terms of velocity?

Isn't acceleration the change in velocity over time?

Exactly! Acceleration is indeed defined as the time derivative of velocity. Now, when we discuss fluids, acceleration isn't just due to time-varying speeds but also due to changes in the velocity field itself. This is where convective acceleration comes into play.

How does that work? Can you give an example?

Great question! Imagine fluid particles moving through a pipe where the flow speed changes at different points. As these particles move, they experience acceleration not just from speeding up or slowing down, but also because they are entering areas where the velocity is different. This spatial difference in velocity is termed convective acceleration.

So, it's like going through a wind tunnel where speed varies?

Exactly! You can think of it as a change in the airflow around you. This leads us to understand local versus convective acceleration. Local acceleration refers to changes in velocity at a fixed point, while convective acceleration relates to how the flow velocity varies in space. Does that make sense?

Yes, I think so. Can you summarize these two types?

Sure! Local acceleration is about how velocity changes at a specific point, and convective acceleration is about how moving through varying velocity fields affects acceleration. Together, they give a complete picture of how fluids behave. Great discussion!
Mathematical Representation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s dive into the mathematics behind convective acceleration. Can anyone remember what the Taylor series does?

It approximates functions using their derivatives at a point.

Correct! When we apply it to fluid dynamics, the Taylor series helps us express changes in velocity over time as well as in various spatial dimensions.

But how do we connect that to local and convective acceleration?

Good question! By considering a Taylor series of velocity functions with respect to space and time, we can segregate these accelerations mathematically, leading us to the equations that define both components of acceleration. It’s about understanding the role of position versus time.

So, the series helps us break down complex behaviors into simpler parts?

Yes, precisely! This breakdown is fundamental to apply physics' principles in real-world scenarios, such as aerospace or ocean currents.

Can we visualize that?

Absolutely! Using vector plots, we can illustrate how the different components of acceleration vary across a fluid flow. This visualization is crucial for comprehending fluid behavior under different conditions.
Eulerian and Lagrangian Perspectives
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, we'll discuss Eulerian and Lagrangian frameworks. Who can explain the difference?

Eulerian focuses on specific locations in space while Lagrangian follows individual particles.

Excellent! In Eulerian, we observe how a fluid's properties change at fixed points. In contrast, Lagrangian allows us to track the motion of specific fluid particles.

How does convective acceleration fit into both perspectives?

Great point! In the Eulerian approach, convective acceleration manifests as changes in velocity fields at various fixed points, while in Lagrangian, it involves how particles behave as they travel through these variable fields.

So, which approach is more useful?

It depends on the situation. Eulerian is often simpler for flow fields, while Lagrangian provides detailed insights about particle dynamics. Understanding both methods allows us to analyze fluid motion comprehensively.

Could we solve some equations next?

Absolutely! Let’s apply these concepts to practical problems to solidify our understanding of convective acceleration.
Real-World Applications
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've covered the fundamentals, let’s discuss some applications. Why do you think understanding convective acceleration is important?

I think it helps in designing better fluid systems like pipes or aircraft.

Exactly! In engineering, applying convective acceleration principles can optimize performance in various systems including hydraulic systems, weather modeling, and vehicle aerodynamics.

What about environmental systems?

Great thought! In environmental science, understanding how pollutants disperse in water bodies also relies on these principles. It helps predict the spread of contaminants.

Can we see real-time examples?

Certainly! Modern simulations using computational fluid dynamics (CFD) provide visual representations of flow and acceleration, allowing us to study complex fluid behaviors in real scenarios.

This is really interesting!

I'm glad you think so! The applications of convective acceleration are vast and vital for many industries. Always remember, the understanding of how fluids behave can lead to innovative solutions in engineering and environmental protection!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Convective acceleration results from the spatial variation of velocity in a flow field, leading to changes in acceleration at a point in a fluid. The section explains the breakdown of acceleration into local and convective components, using foundational concepts such as the Taylor series and material derivatives.
Detailed
Detailed Summary
In fluid dynamics, the concept of convective acceleration is critical for understanding motion within a fluid. This section elaborates on how acceleration in a fluid is not merely due to time changes in velocity, but also due to changes in the velocity field itself across space. The section defines acceleration mathematically as the time derivative of velocity and discusses how this can be intricately linked to both local and convective acceleration.
The key takeaway is that acceleration can be expressed as:
- Local Acceleration, which is the change in velocity at a specific point in a fluid over time.
- Convective Acceleration, which occurs due to the movement of fluid particles through regions of different velocity, leading to changes in acceleration based on the spatial position of particles.
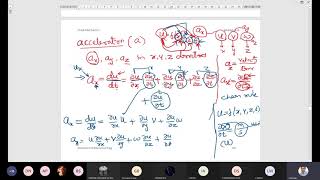
To further explain these concepts, the section utilizes Taylor series expansions to delineate particle-level behavior under Newtonian physics, emphasizing the importance of understanding the velocity gradients in three dimensions (x, y, z) as well as time contributions. By expressing acceleration in terms of vector calculus, and utilizing the del operator (also known as the gradient operator), the text lays the groundwork for depth in fluid mechanics, preparing students for complex applications in both Eulerian and Lagrangian frameworks.
Youtube Videos
![Convective Acceleration Animation [Fluid Mechanics]](https://img.youtube.com/vi/7FuufEU6i4Y/mqdefault.jpg)
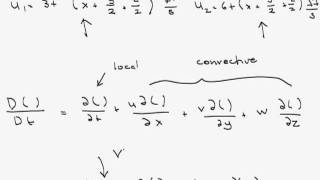
![Fluid Kinematics -10 [Solved problems on Total Acceleration, temporal and convective acceleration]](https://img.youtube.com/vi/uCwy59bshSE/mqdefault.jpg)



![Fluid Kinematics - 4 [Total acceleration , temporal and convective acceleration in fluid flows]](https://img.youtube.com/vi/rt7mBeixD2k/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Acceleration at a Particle Level
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, let us look at the particle levels, if I had to find out what is the acceleration of the fluid particles? Is nothing else as a time derivative of velocity of the particles.
Detailed Explanation
At the particle level, acceleration is defined as the change in velocity over time. This means that to understand how fast a particle is accelerating, we look at how its velocity changes over time. In simpler terms, if a particle moves faster or slower, that change is what we measure as acceleration.
Examples & Analogies
Think of a car accelerating from a stoplight. When the light turns green, the car starts from a complete stop and speeds up over time. The change in how quickly the car is going, from being stopped to speeding up, represents its acceleration.
Local Components of Acceleration
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
At the particle levels, you will have these velocities with a variability in positions and the time because of that though when you define a; derivative with respect to time you will have a local component.
Detailed Explanation
When we talk about acceleration, we must consider that it can vary based on the position of the particle in space and over time. This means that if we were to look at different areas, the acceleration of fluid particles could be different, creating what we call 'local acceleration' based on their specific positions and how they change over time.
Examples & Analogies
Imagine a group of runners on a track. Some runners may start earlier or later depending on their position on the track. The acceleration of each runner might be different based on where they are at any given time, just like particles in a fluid.
Taylor Series and Accelerations with Multiple Variables
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This is nothing else if you are considering is a 2 variables like I just discussed you the Taylor series; in this case, I have a Taylor series of 4 variables: the x, y, z, and the t.
Detailed Explanation
The Taylor series is a mathematical tool that allows us to approximate functions. In this context, it helps us understand fluid motion by expanding the variables affecting particle acceleration (x, y, z, and time) into a series. This means we can express complex fluid behaviors in terms of simpler polynomial functions, making it easier to calculate things like acceleration.
Examples & Analogies
Imagine a series of steps leading up a hill. Each step allows you to go higher, just as a Taylor series allows us to build up the complexity of a fluid’s movement in manageable chunks. Just like taking one step at a time makes climbing easier, using polynomial approximations makes understanding fluid motion simpler.
Local and Convective Acceleration
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you look at this way, what is that? ... two components; one is local acceleration component and the other is convective acceleration.
Detailed Explanation
When we analyze fluid movement, we can divide acceleration into two parts: local acceleration, which is the change in velocity at a fixed point over time, and convective acceleration, which accounts for changes in velocity due to the particle's movement through a velocity field. Combining these offers a complete picture of how particles move within the fluid.
Examples & Analogies
Consider a river. A leaf floating on the river experiences local acceleration as the water flows past it at a constant speed (local), while it also travels downriver, increasing its position along the river due to the current (convective). Both speeds contribute to how fast and where the leaf moves.
Mathematical Representation of Acceleration
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, mathematically we can represent the local accelerations and the convective acceleration component.
Detailed Explanation
Mathematically, we can express both local and convective accelerations using derivatives. Local acceleration can be viewed simply as the change in velocity at a point, while convective acceleration includes the gradients of the velocity field, capturing more complex movement as particles move through different areas of velocity.
Examples & Analogies
Think of a weather map showing wind speeds at different locations. If one area has higher wind speed, it’s as if the leaves in that part of a park are being pushed harder compared to others. The math is like interpreting this data to predict how fast the leaves will be blown away based on both local wind speed and the ‘push’ from surrounding winds.
Key Concepts
-
Convective Acceleration: This involves understanding how acceleration changes due to velocity variations in space rather than time alone.
-
Local Acceleration: The acceleration occurring at a point in a fluid, due to a change in the velocity of that fluid over time.
-
Eulerian and Lagrangian Frameworks: Two perspectives for analyzing fluid motion, one focusing on fixed points and the other on moving particles.
-
Taylor Series: A mathematical tool used to approximate fluid behavior under varying conditions.
Examples & Applications
In a pipe flowing from high pressure to low pressure, fluid particles will accelerate differently based on their position in the pipe due to varying velocity fields.
During a storm, the air particles experience convective acceleration as they move through areas of varying wind speeds, which can lead to turbulence.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In the fluid's dance, flows change their pace, convective moves take the lead in the race.
Stories
A stream of water in a park experiences pressure changes as it flows through different terrains, showing how its speed and direction continuously adapt to new environments, illustrating local and convective acceleration.
Memory Tools
L-C for Local and Convective: Local means ‘time’ changes at a point, Convective is about ‘space’ flow, just remember L-C!
Acronyms
E-L Axis for Eulerian & Lagrangian
for observing flows at a point
for following the flow's path.
Flash Cards
Glossary
- Convective Acceleration
Acceleration resulting from the movement of fluid particles through varying velocity gradients in a flow field.
- Local Acceleration
The change in velocity of a fluid particle at a fixed location over time.
- Eulerian Perspective
An approach to fluid dynamics focusing on changes in fluid properties at fixed points in space.
- Lagrangian Perspective
An approach to fluid dynamics following the trajectory of individual fluid particles.
- Taylor Series
A mathematical representation of a function expressed as an infinite sum of terms calculated from the values of its derivatives at a single point.
Reference links
Supplementary resources to enhance your learning experience.
