Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Newton's Second Law and Fluid Mechanics
Unlock Audio Lesson
Today, we are going to discuss Newton's second law as it applies to fluid mechanics. Can anyone tell me what Newton's second law states?
It states that force equals mass times acceleration!
Exactly! And what are the vector components that we consider for acceleration and force in fluid mechanics?
Acceleration is also a vector, and it depends on the direction of the fluid’s flow.
Correct! Remember the acronym 'F=ma'—Force equals mass times acceleration. This is key when analyzing fluid particles. Now, how do we derive acceleration for these particles?
We differentiate velocity with respect to time!
Great! That's right. Acceleration is the time derivative of velocity, which we can break down into multiple directions.
Let's recap: Newton's law is foundational, and acceleration in fluid dynamics involves understanding both local and convective accelerations.
Acceleration Components
Unlock Audio Lesson
Now that we've covered Newton’s second law, let’s discuss the different components of acceleration we encounter in fluid mechanics. Can anyone name them?
Local acceleration and convective acceleration?
Exactly! Local acceleration measures how much the velocity changes at a specific location, while convective acceleration accounts for velocity changes due to the flow itself—think of how a river flows faster in some areas compared to others. How do we mathematically represent these?
Using derivatives in our equations, right? Like in a Taylor series?
That’s correct! Taylor series help us understand the behavior of functions with multiple variables, like position and time, allowing us to compute these components accurately. Can anyone explain why we need both types of acceleration?
We need both because they give us a complete picture of how the fluid behaves under different conditions.
Great summary! Understanding both allows for thorough analysis in fluid dynamics. Remember to visualize these concepts with flow diagrams for better retention.
Material Derivative
Unlock Audio Lesson
Now let's move on to the material derivative. Why is this concept significant when we analyze fluid behavior?
It shows how quantities like velocity or pressure change as we move with the fluid particles?
Exactly! The material derivative combines local and convective changes. Can anyone give me an example of how we might use it in practice?
We could use it to study how the velocity of a fluid changes around an object, like a boat.
Very good example! Calculating these derivatives is essential for predicting how fluid flows will behave. Remember, the material derivative connects local properties like velocity with the overall motion of the fluid.
In summary, the material derivative is a powerful tool in our analysis arsenal. It helps relate various fluid properties and understand their implications.
Practical Application and Examples
Unlock Audio Lesson
Let's solidify our understanding by solving some practical problems regarding material acceleration. Who’s ready for a challenge?
I am! What do we need to do first?
Great enthusiasm! First, we need a velocity field to compute material accelerations. For example, if we have a velocity field described by V = zi + xj +yk, how would we start?
We identify the velocity components and then differentiate them!
Right again! This process lays the foundation for calculating both local and convective accelerations. Who can tell me how we can interpret the results after calculating?
We can determine how these accelerations affect motion and stability in our fluid flow!
Exactly! These applications help us understand how real-world fluid systems evolve over time.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore Newton's second law in the context of fluid mechanics, introducing material acceleration as a time derivative of velocity. The discussion emphasizes the differentiation of velocity components in relation to spatial variables, highlighting local and convective acceleration concepts.
Detailed
Detailed Summary
This section delves into the foundational principles of fluid mechanics, particularly focusing on material acceleration. The discussion begins by recalling Newton's second law, stating that force is equal to mass multiplied by acceleration, emphasizing that both force and acceleration are vector components.
We explore how to find the acceleration of fluid particles, defined as the time derivative of the particle's velocity. The relationship between position, velocity, and time is crucial here, as it allows us to establish the components of velocity in different directions (x, y, and z).
The section introduces Taylor series expansion for multi-variable functions to aid in understanding acceleration across varying positional parameters. It subsequently illustrates how to derive acceleration components in both Lagrangian and Eulerian perspectives, discussing local and convective accelerations as critical concepts. Local acceleration refers to the change in velocity at a particle's position, while convective acceleration accounts for variations due to gradients in the velocity field.
In conclusion, the material derivative is introduced as a means to quantify changes in properties like density and pressure concerning time, illustrating how these derivatives reflect the behavior of fluid particles. A practical problem example further solidifies understanding of how to compute material acceleration in a given velocity field.
Youtube Videos
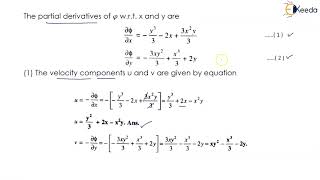
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Newton's Second Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, similar way if I am looking at Newton's second law also see that force is equal to mass into acceleration, force is vector component, acceleration is the vector component, okay and both are the parallels okay, so force and the vector, at the particle levels like in solid mechanics, the force we can put is mass into acceleration.
Detailed Explanation
Newton's second law states that Force (F) is equal to mass (m) multiplied by acceleration (a), which can be expressed as F = m * a. Here, both force and acceleration are considered vector quantities, meaning they have both magnitude and direction. This relationship helps in understanding how forces behave at the particle level, particularly in solid mechanics, where the acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass.
Examples & Analogies
Think of a car accelerating. The force applied by the engine increases the car's speed; however, the same force will accelerate a lighter car more than a heavier one when both are pushed with the same force. This illustrates how mass and acceleration are linked through force.
Finding Acceleration of Fluid Particles
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let us look at the particle levels, if I had to find out what is the acceleration of the fluid particles? Is nothing else is a time derivative of velocity of the particles, as you know it from class 10, 11th and 12th I am just doing this time derivative of the velocity; particle velocities with respect to time and that is what represents the accelerations.
Detailed Explanation
Acceleration of fluid particles can be defined as the rate of change of velocity with respect to time. Mathematically, this is represented as a derivative: a = dv/dt, where 'a' is acceleration, 'v' is velocity, and 't' is time. In fluid dynamics, this means monitoring how the velocity of individual particles in a fluid changes over time, which is crucial for understanding fluid motion and behavior.
Examples & Analogies
Imagine riding a bike. If you start pedaling harder (increasing acceleration), your speed increases. The change in your speed (velocity) over time illustrates the concept of acceleration in fluid dynamics, analogous to how bike riders can adjust their pace.
Velocity Variability Across Different Directions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if you look at this the velocities has a variability in a positions and the time because of that though when you define a; derivative with respect to time you will have a local component okay, you will have a with a x particle directions, y particle directions and z particle direction.
Detailed Explanation
In fluid dynamics, velocity can vary not only with time but also with position in space (x, y, z directions). Therefore, when evaluating acceleration, one must consider the local components: how velocity changes in each spatial direction over time. These local changes can be represented using vector components, indicating that fluid flow can be unsteady and complex.
Examples & Analogies
Imagine a river flowing over a rocky bed. The water moves faster over some rocks and slower around others. This varying speed is akin to the 'velocity variability' across directions. When analyzing flow, we look at how fast the water is moving at different points and times.
Taylor Series for Velocity Expansion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is nothing else if you are considering is a 2 variables like I just discussed you the Taylor series, if you remember it defining for the 2 variables in this case, I have a Taylor series of 4 variables the x, y, z and the t.
Detailed Explanation
The Taylor series is a mathematical tool used to approximate functions. In the context of fluid dynamics, it can expand a function around a point using its derivatives. When applied to functions of multiple variables (like three spatial dimensions and time), it helps in representing how velocity and subsequently acceleration may vary in a fluid. This approximation is essential for simplifying complex fluid equations.
Examples & Analogies
Think of a Taylor series like a recipe for approximating a flavor based on a few primary ingredients. Just as a few key flavors can approximate a dish's overall taste, using derivatives allows us to approximate complex fluid behavior based on simpler components.
Local and Convective Acceleration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
That means, with respect to time, how much of variations and when you are considering that you do not consider the variability in the x and y, z that what is called the local accelerations but this component if you look it, it is called convective or advective acceleration that because the particles are having different velocity gradient.
Detailed Explanation
In fluid dynamics, local acceleration represents how the velocity of a particle at a specific point in space changes over time. In contrast, convective (or advective) acceleration takes into account the spatial gradient of velocity, meaning it considers how particles are moving through areas with varying flow speeds. Both components are essential for analyzing fluid motion.
Examples & Analogies
Consider a crowd at a concert. Local acceleration would refer to how fast an individual starts moving faster or slower with the music. In contrast, convective acceleration exemplifies how the entire crowd may move in waves, carrying individuals with varying speeds through different sections.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Newton's Second Law: A fundamental principle stating that force is equal to mass times acceleration.
-
Local vs. Convective Acceleration: Local acceleration is a measure of how velocity changes at a specific point, while convective acceleration accounts for changes in velocity due to flow.
-
Material Derivative: Describes the change in fluid properties as fluid particles move through space and time.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a fluid particle's velocity changes from 5 m/s to 15 m/s in 2 seconds, the local acceleration can be calculated as (15-5)/2 = 5 m/s².
-
When analyzing flow around an object, the material derivative of velocity helps to understand how the speed of flow changes as it interacts with the object.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Acceleration can flow, both local and convective show. Newton said it best, 'F=ma' passes the test.
📖 Fascinating Stories
-
Imagine a river where the water speeds up as it flows over rocks. The water accelerates locally at each rock, while convectively it shifts speeds as it moves downstream.
🧠 Other Memory Gems
-
V-L-C: Velocity changes lead to Local & Convective accelerations.
🎯 Super Acronyms
M-A-D
- Material Acceleration Derivative—helps remember the components of fluid acceleration.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Material Acceleration
Definition:
The acceleration experienced by a fluid particle as it changes position or velocity over time.
-
Term: Local Acceleration
Definition:
Acceleration that arises from a change in the velocity of a fluid particle at a given point in space.
-
Term: Convective Acceleration
Definition:
Acceleration that occurs due to changes in velocity as a fluid moves through space.
-
Term: Material Derivative
Definition:
The derivative of a quantity that reflects the change with respect to time as experienced by a particle moving with the flow.