Motion and Deformation of Fluid Particles
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Newton's Second Law in Fluid Mechanics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to relate Newton's second law, which states that Force equals mass times acceleration, to fluid particles. Can anyone tell me how this might look at the particle level?

Would it still involve finding acceleration like we do in solids?

Exactly! In fluids, acceleration is also derived as the time derivative of the velocity of particles. Can someone define what acceleration is?

Acceleration is the rate of change of velocity with time, right?

That's right! In fluids, velocity can change not just with time but also with position, which can complicate things. This brings us to how we measure it, using local and convective accelerations.

What's the difference between local and convective acceleration?

Good question! Local acceleration is the velocity change at a certain point in the fluid over time, while convective acceleration accounts for the variation of velocity due to the particle's motion through the velocity field.

So, local means changes over time at a fixed point, and convective means changes due to moving through varying velocities?

Exactly! Remember the acronym LCV — Local is Change over Time, Convective is Change due to Velocity. Great summary, everyone!
Application of Taylor Series in Fluid Dynamics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's dive deeper into fluid behavior by discussing the Taylor series application. Who remembers what Taylor series does?

It expands functions into polynomials based on derivative values at a point, right?

Exactly! In fluid dynamics, it helps us represent the velocity fields with respect to four variables: x, y, z, and time. Can anyone see how this could be useful?

I think it helps us understand changes in velocity and position over time!

Exactly! By doing this expansion, we can derive conditions for fluid particles and understand how their velocities vary spatially and temporally.

So, can we apply these ideas to see how pressure influences these motions too?

Absolutely! The velocity components tie directly to pressure gradients and create a complete picture of fluid behavior.

What would happen if we didn't consider these variables together?

Ignoring any of these variables could lead to incomplete or incorrect models of fluid behavior. So always remember to consider all dimensions and time! Let’s summarize our key points through our acronym, 'VLOD' — Velocity, Local, and Oscillations in Dimensions.
Calculating Local and Convective Accelerations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s look at how we can calculate these accelerations. We have a velocity vector for a fluid with components u, v, and w. How do you suggest we approach this?

We can differentiate the velocity components to find the local acceleration.

Correct! And for convective acceleration, how do we handle it?

We look at the velocity gradients in the x, y, z directions and use partial derivatives.

Right again! Remember, convective acceleration accounts for changes caused by fluid motion. Let’s calculate a local and convective acceleration using a sample velocity field.

That sounds great! I’m eager to put these concepts into practice.

Before we dive in, remember our acronym 'VGLC' — Velocity Gradients Leading to Convective changes. Let’s keep that in mind!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section elaborates on the concepts of force, acceleration, and velocity at the particle level in fluid mechanics. It introduces the mathematical frameworks essential for understanding how fluid particles move and deform under different conditions, including local and convective accelerations.
Detailed
In this section, we delve into the intricate relationship between motion, force, and deformation of fluid particles by applying Newton's second law. The foundational equation, F = m*a, is adapted to fluid mechanics, illustrating how fluid particle acceleration is derived as the time derivative of particle velocity. The section discusses the need to consider velocity derivatives with respect to not just time but also spatial dimensions (x, y, z), preserving the fluid's dynamical behavior. Introducing Taylor series expansion captures these variations, emphasizing the local acceleration and convective acceleration within the fluid's velocity field. Local acceleration describes the change in velocity at a specific point in time, while convective acceleration considers how particle velocities vary due to spatial fluid dynamics. By calculating these types of accelerations in Eulerian and Lagrangian frameworks, this section lays the groundwork for further exploration of fluid mechanics concepts such as pressure and vorticity.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Acceleration in Fluid Particles
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, let us look at the particle levels; if I had to find out what is the acceleration of the fluid particles? Is nothing else is a time derivative of velocity of the particles. Particle velocities with respect to time represent the accelerations at the particle levels.
Detailed Explanation
The acceleration of fluid particles can be defined as the change in velocity over time. When we talk about particles in a fluid, their velocities change with time due to motion. Therefore, to find out how fast those particle velocities are changing, we take the derivative with respect to time. This concept is straightforward: if you know how the velocity of an object increases or decreases over time, you can determine its acceleration simply by checking how much the speed (or direction) changes as time passes.
Examples & Analogies
Imagine you're driving a car and you start going faster. At the beginning, you're at a standstill. When you press the gas pedal, your speed increases. The rate at which your speed increases is your acceleration. In the same way, fluid particles accelerate as their velocities change over time, which is essential in understanding fluid motion.
Vector Components of Acceleration
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now, if you look at this, the velocities have variability in positions and time because of that, when you define a derivative with respect to time, you will have a local component in x, y, and z directions.
Detailed Explanation
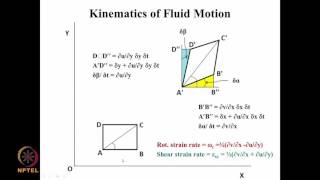
When discussing fluid motion, it's not just about how fast a particle is moving, but also about how that movement varies in space. This means that at different points in the fluid (in the x, y, and z directions), particles can experience different velocities. Consequently, when we measure acceleration, we must consider how these variations across three dimensions affect the overall motion of the fluid. Thus, the acceleration can be broken down into components that account for how particles are moving differently in each of these three dimensions.
Examples & Analogies
Think of a river flowing downhill with different depths. In one area, the water flows quickly because it's shallow and steep, while in another area, it's deep and slow. If you were to measure the speed of the water at various points, you’d find different velocities, and thus different accelerations. Each point along the river has a unique velocity that changes depending on its position in the flow.
Taylor Series Expansion in Fluid Dynamics
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This is nothing else if you are considering two variables like I just discussed, you will have a Taylor series of four variables: x, y, z, and t. If you expand it and take only these four terms, you will get this component.
Detailed Explanation
The Taylor series is used in fluid mechanics to expand functions near a certain point. In this case, we're considering the fluid properties as functions of their position in three dimensions (x, y, z) and time (t). When you apply the Taylor series, you can approximate these functions and understand how they behave locally near a specific point in space and time. This way, you can represent the complex behavior of fluid motion as a sum of simpler terms, making calculations and predictions more feasible.
Examples & Analogies
Imagine you're examining how a small section of a river behaves at various points right around a bend. Let's say at a particular point, you know the speed of the water and how it changes. The Taylor series helps you understand the flow around the bend by approximating how the water will move not far from that point based on the speed and direction you already measured.
Local and Convective Accelerations
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We can define two components of acceleration: local acceleration, which occurs due to changes in velocity with respect to time at a fixed point, and convective acceleration, which arises due to changes in velocity across different locations in space.
Detailed Explanation
Local acceleration refers to how the velocity of a single fluid particle changes at a specific position over a short period of time. On the other hand, convective acceleration takes into account how the velocity varies across the fluid – for example, if a particle moves into an area with a different speed. Therefore, a complete understanding of fluid motion requires analyzing both types of acceleration, as they together determine the overall behavior of the fluid flow.
Examples & Analogies
Consider a traffic scenario: If you're driving in one direction and stop at a red light (local acceleration), you experience a change in your speed. Now imagine merging into a fast-moving lane (convective acceleration). Your speed is changing not because of your own acceleration, but because you're moving from a slower to a faster moving stream of traffic. Both local and convective accelerations influence your driving experience, just like they do for fluid particles.
Key Concepts
-
Newton's second law: Fundamental principle applicable to fluid particles just as to solids.
-
Local Acceleration: Change in velocity at a point in time.
-
Convective Acceleration: Change in velocity due to motion through varying fields.
-
Velocity Field: Representation of how velocity changes throughout the fluid.
Examples & Applications
Given a fluid velocity field V = zi + xj +yk, find the material acceleration vector at specific locations (1, 4, 1).
In a fluid where velocities are defined as u = -3x, v = 2y, w = z, evaluate if the flow is steady and calculate accelerating components.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In the fluid's dance, motion's key, Local time change for you and me. Convective flow as particles glide, Through spaces where their speeds reside.
Stories
Once there were fluid particles, each moving in their unique patterns. One day, they learned about local acceleration when time changed their speed. Traveling through various spaces, they discovered convective acceleration while adapting to different flow speeds in their journey!
Memory Tools
Remember the acronym 'LCC' — Local means change over time, Convective means change due to movement.
Acronyms
Use 'VLOD' to remember - Velocity, Local, Oscillation, Dimensionally.
Flash Cards
Glossary
- Acceleration
The rate of change of velocity of a fluid particle over time.
- Local Acceleration
The acceleration at a specific point in the fluid due to changes over time.
- Convective Acceleration
Acceleration due to the variation of velocity experienced by moving through different points in the fluid.
- Velocity Field
A mathematical representation of the velocity of fluid particles across a region.
- Taylor Series
A mathematical series used to represent a function as an infinite sum of terms based on the function's derivatives.
Reference links
Supplementary resources to enhance your learning experience.
