Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Acceleration Components
Unlock Audio Lesson
Today we're going to discuss local and convective acceleration components in fluid dynamics. Can anyone explain what acceleration means in this context?
I think acceleration is the rate at which velocity changes over time.
Exactly! Acceleration is about how quickly velocity changes. Now, we categorize these changes into local and convective acceleration. Local acceleration is due to time changes at one point. Can anyone give me an example?
Isn't it like measuring how a water droplet's speed changes at a certain position?
Great example! And what about convective acceleration?
I think it's when the droplet moves into a region where the flow speed is different.
Correct! Convective acceleration looks at how changin positions affect velocity. Remember the acronym 'CATT' — Convective Acceleration = Time + Transition.
That will help me remember it! Can we look at the equations next?
Absolutely! We'll discuss how we mathematically express these components.
In summary, local acceleration is tied to velocity changes over time at a stationary point, while convective acceleration involves movement through varying velocity fields.
Mathematical Representation
Unlock Audio Lesson
Let's delve into the equations that represent local and convective accelerations. Can someone explain how we derive these from velocity definitions?
We start with velocity as a function of position and time, right? Like `v = f(x,y,z,t)`?
Exactly! The local acceleration is the partial derivative of velocity with respect to time. What does that tell us?
It shows how the speed changes at a specific location over time.
Well said! Now, how about the convective acceleration?
It’s a partial derivative with respect to space, which shows how velocities change as particles move.
Right! This relationship helps in visualizing how fluid flows change as particles transition across different regions. Remember, the two components together help explain fluid motion effectively.
To conclude this session, local acceleration captures time-based changes at static points, while convective acceleration describes spatial changes in a dynamic flow.
Applications in Fluid Dynamics
Unlock Audio Lesson
How do local and convective accelerations appear in real-world fluid dynamics situations? Can anyone think of an example?
What about river currents? The water speeds change both over time and as you move along the river?
Exactly! In such a scenario, local acceleration reflects changes in flow speed at a bank, while convective acceleration occurs when water moves into faster flows near the middle of the river.
That makes sense! What about in meteorology or predicting cyclone behavior?
Great observation! Meteorologists often account for changes in both velocity and pressure gradients to forecast weather. This interplay directly shows local acceleration effects at a specific time and convective accelerations due to spatial shifts.
In summary, applications extend from rivers to weather predictions, showcasing the importance of both types of acceleration in analyzing fluid behavior.
Critical Thinking and Problem-Solving
Unlock Audio Lesson
Let's apply our knowledge practically. If given a velocity field, how can we find local and convective acceleration? Who can walk me through this process?
We substitute velocity expressions into the equations for each type of acceleration and differentiate them.
Good! If `v(x,y,z,t) = x^2 + y^2 + z^2`, what would the local acceleration be?
That would be the partial derivative of that expression with respect to time, but there’s no time dependency here.
So, what does that mean for local acceleration?
It would be zero since that velocity doesn't change over time.
Correct! Now, what about convective acceleration?
We’d find the partial derivatives with respect to x, y, and z.
Exactly! Applying these derivatives helps us understand complex fluid behaviors. Let’s summarize: local acceleration can be zero in steady systems, while convective acceleration arises from fluid flow through varied velocities.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores the concepts of local and convective accelerations in fluid mechanics, explaining how these components are derived from velocity changes over time and space. Emphasis is placed on understanding their mathematical representation, significance in different reference frames, and examples illustrating their applications.
Detailed
Local and Convective Acceleration Components
In fluid dynamics, understanding motion requires examining accelerations which can be categorized into local and convective (or advective) components. Local acceleration refers to changes in a fluid particle's velocity at a fixed point, influenced purely by time-dependent velocity variations, while convective acceleration considers variations in velocity due to the spatial movement of fluid particles through different velocity fields.
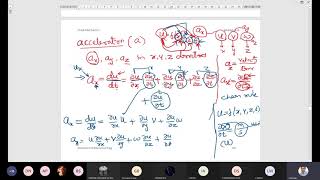
Using Newton's second law as a foundation, the relationship between force, mass, and acceleration introduces the concept of accelerations being vector quantities dependent on positional and temporal variations in velocity.
In more complex fluid scenarios where fluid flow is assessed, two forms of acceleration components are important:
1. Local Acceleration: The change in velocity at a specific point over time, represented as a partial derivative of the velocity vector with respect to time.
2. Convective Acceleration: The change in velocity experienced by a particle moving through a velocity field, computed from the spatial derivatives of velocity as fluid properties change throughout the flow.
In mathematical terms, these are illustrated via Taylor series expansions in three-dimensional spatiotemporal frameworks, emphasizing how derivatives capture these dynamical behaviors. Understanding these differences is vital in analyzing fluid dynamics under various conditions, linking Eulerian and Lagrangian frames of reference effectively.
Youtube Videos
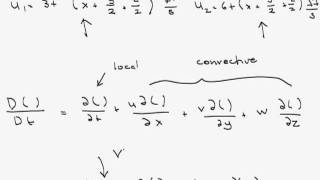
![[12] Local and Convective Acceleration | Fluid Mechanics Lecture for GATE by Pranshu Mahajan](https://img.youtube.com/vi/_6uq1Ti5PNk/mqdefault.jpg)
![Convective Acceleration Animation [Fluid Mechanics]](https://img.youtube.com/vi/7FuufEU6i4Y/mqdefault.jpg)
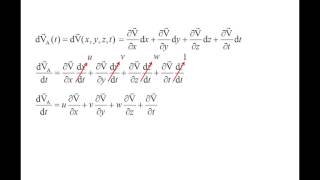
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Newton's Second Law and Acceleration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, similar way if I am looking at Newton's second law also see that force is equal to mass into acceleration, force is vector component, acceleration is the vector component, okay and both are the parallels okay, so force and the vector, at the particle levels like in solid mechanics, the force we can put is mass into acceleration.
Detailed Explanation
This chunk discusses Newton's second law, which states that force is equal to mass times acceleration. This is essentially a vector relationship, indicating that both force and acceleration have specific directions. When addressing forces at the particle level, such as in solid mechanics, we can apply this concept similarly to fluids by considering the acceleration of fluid particles in relation to mass.
Examples & Analogies
Imagine pushing a shopping cart. The harder you push (force), the faster it goes (acceleration). If you have a heavier cart (more mass), you must push harder to achieve the same acceleration. This relationship mirrors how fluid particles behave when subjected to forces.
Acceleration of Fluid Particles
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let us look at the particle levels, if I had to find out what is the acceleration of the fluid particles? Is nothing else is a time derivative of velocity of the particles, as you know it from class 10, 11th and 12th I am just doing this time derivative of the velocity; particle velocities with respect to time and that is what represents the accelerations, at the particles levels you will have these.
Detailed Explanation
In this part, the text explains that to find the acceleration of fluid particles, we need to calculate the time derivative of the velocity of those particles. Essentially, acceleration represents how quickly a particle's velocity changes over time. This concept is foundational in physics and helps to quantify how fluid speed varies.
Examples & Analogies
Consider riding a bike. When you start pedaling harder (increasing your velocity), initially, you may reach your desired speed quickly (high acceleration). However, as you start nearing your maximum speed, it takes longer to increase speed (decreasing acceleration) because you are already moving fast.
Local and Convective Acceleration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These components change of the velocities is called convective or advective acceleration component, so this is 2 components; one is local acceleration component and other is convective acceleration. In vector (()) (45:37), we can very simple way represented the local accelerations and the convective acceleration component.
Detailed Explanation
Here, the text introduces two types of acceleration components relevant in fluid dynamics: local acceleration and convective (or advective) acceleration. Local acceleration refers to the changes in velocity at a specific point in the fluid related to time. In contrast, convective acceleration concerns the changes in velocity as particles move through space and encounter varying velocity fields.
Examples & Analogies
Think of a river with a current. If you're swimming without moving, you're experiencing local acceleration based on how the current affects your position over time. However, if you start swimming downstream and your speed changes due to the current's flow, that's an example of convective acceleration as your position shifts in the fluid.
Total Acceleration in Eulerian and Lagrangian Perspectives
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, as this fluid having this velocity field, we can compute the accelerations field, we can compute this material derivative of the pressures, we can compute the material derivative of density with the same format, we can compute and we can solve the problems in this way.
Detailed Explanation
This chunk discusses how fluid flows can be analyzed through two perspectives: Eulerian and Lagrangian. The Eulerian perspective focuses on specific points in space, looking at how fluids behave at given locations. In contrast, Lagrangian focuses on individual particles as they move through the fluid flow. Both methods can compute acceleration fields, material derivatives, density, and pressure.
Examples & Analogies
If you think of a crowded highway, the Eulerian perspective is like observing traffic from a fixed point on the side of the road, while the Lagrangian perspective is like being in a single car and noticing how that one vehicle interacts with traffic. Both views provide important insights into the movement of vehicles (or fluid particles).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Local Acceleration: Change of velocity at a specific location over time.
-
Convective Acceleration: Change of velocity due to fluid particles moving through varying speed regions.
-
Eulerian vs. Lagrangian: Two perspectives in fluid dynamics for analyzing flow behaviors and properties.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
River current dynamics demonstrating local acceleration changes at one bank vs. convective acceleration as water flows into stronger currents in the middle.
-
Weather prediction models using local acceleration for time-variable data and convective acceleration for spatial movement within atmospheric flows.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Local speed changes at the same place, Convective shifts as you change space.
📖 Fascinating Stories
-
Imagine a leaf floating down a river. At one point, the water slows down, and locally the leaf's speed drops. But as it drifts downstream into a quicker current, it speeds up due to convective effects.
🧠 Other Memory Gems
-
Use 'LCT' to remember: Local = Change over Time, Convective = Change during Transition.
🎯 Super Acronyms
LAPC
- Local Acceleration = Point in Time
- Convective = Change via Position.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Local Acceleration
Definition:
The change in fluid particle velocity with respect to time at a fixed position.
-
Term: Convective Acceleration
Definition:
The change in velocity experienced by a fluid particle due to its movement through a spatial velocity gradient.
-
Term: Eulerian Description
Definition:
A viewpoint in fluid dynamics that focuses on specific locations in space where properties are measured as functions of time.
-
Term: Lagrangian Description
Definition:
A viewpoint that follows individual fluid particles and studies their motion over time.
-
Term: Velocity Field
Definition:
A vector field that represents the velocity of fluid at various points in space.