Material Derivative of Density and Pressure
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Material Derivatives
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to explore material derivatives, which will help us understand how properties like density and pressure behave in moving fluids. Let's start by defining what a material derivative is.

Is a material derivative different from a regular derivative?

Great question! Yes, a regular derivative measures how a quantity changes at a fixed point, while a material derivative accounts for the motion of the fluid itself. It's essential for analyzing changes along the flow.

What parts does it consist of?

The material derivative includes local acceleration and convective acceleration. Remember this acronym: **L and C**. 'L' for local and 'C' for convective.

So, local acceleration is about changes over time at a point?

Exactly! Local acceleration looks at how the velocity changes at that specific point over time. On the other hand, convective acceleration looks at the change as the fluid flows through space.

What would be the significance of understanding these concepts?

Understanding material derivatives allows us to predict fluid behaviors and phenomena, such as how pressure changes in moving fluids.

To summarize, material derivatives provide an essential framework in fluid dynamics by linking changes in density and pressure to both local and convective effects.
Mathematical Representation of Material Derivatives
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s look at the mathematics behind material derivatives. The material derivative of density is given by a specific formula that combines both local and convective changes.

What does the formula look like?

The formula for the material derivative of density can be expressed as: \(\frac{D\rho}{Dt} = \frac{\partial \rho}{\partial t} + \mathbf{u} \cdot \nabla \rho\). This combines the local change and the convective change.

What about pressure? Is it similar?

Absolutely! The material derivative of pressure uses a similar structure. The key difference lies in how pressure influences fluid motion.

Can we see a practical application of this?

Certainly! When we analyze flow in pipes, using these formulas can help us predict how pressure changes at given points based on velocity fields.

It's like a dynamic equation for fluids!

Exactly! It's a dynamic relationship allowing engineers to design better systems by predicting behavior.

So remember, understanding the material derivatives in terms of density and pressure helps in modeling fluid dynamics accurately.
Material Acceleration Component Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let's analyze the acceleration components derived from our earlier discussions. We can represent acceleration in a vector form.

How do you break that down into components?

We break it down into x, y, and z components. Each acceleration can be expressed as \( a_x, a_y, a_z \). Remember: **3D components**.

How can we compute these components?

You can find the components using the derivatives of velocity. This gives you detailed insight into how fluid behaves over time and space.

Any example of how these computations work?

Sure! Let’s solve an example where we compute the material acceleration for a given velocity field. The following equation will help: \( a = \frac{D\mathbf{v}}{Dt} \).

What should we expect in the final result?

The final result will highlight both local and convective components, revealing how the overall acceleration is influenced by both sources.

To summarize, determining the components of material acceleration through vector analysis is crucial in understanding fluid motion.
Application of Material Derivatives
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s apply what we've learned to real-world scenarios. Understanding material derivatives has vast applications in fluid dynamics.

Can we see this in action in an example?

Certainly! Consider the flow of water through a pipe. The material derivative helps us understand how pressure varies along the pipe as fluid flows.

What parameters do we need to consider?

You must account for factors like velocity, density, and the nature of the flow—whether it's steady or unsteady.

Can we perform a problem-solving session?

Yes! Let’s analyze a problem involving a specific velocity field and compute the resulting material derivative effects.

What can we expect from these exercises?

You’ll expect to compute how different factors change the outcomes, enriching your understanding of fluid dynamics.

So to wrap up, applying our knowledge about material derivatives allows us to solve real-world fluid dynamics problems effectively.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, the material derivative concepts in fluid mechanics are introduced, explaining how density and pressure evolve over time along the paths of fluid particles. The focus is on both local and convective components of acceleration, emphasizing their mathematical derivations and implications in fluid dynamics.
Detailed
Material Derivative of Density and Pressure
In fluid dynamics, understanding how properties such as density and pressure change along fluid paths is fundamental. This section covers the material derivative, which expresses the time rate of change of a quantity (like density or pressure) as experienced by a moving particle of fluid.
The mathematical foundation of the material derivative involves both local and convective accelerations. Local acceleration refers to the changes at a point with respect to time, while convective acceleration addresses the changes due to the movement of the fluid particles through space.
We have established the following key points:
1. Velocity as a Function of Space and Time: Velocity changes with respect to all spatial coordinates and time, leading to a multi-variable Taylor series expansion.
2. Definitions of Components: The velocity components are denoted as u, v, and w in the x, y, and z directions, respectively, with acceleration derived from these components.
3. Material Derivative: This derivative encapsulates the total change experienced by a particle, combining local changes due to time and variations from spatial movement. The formulas for the material derivative of density and pressure are given in terms of velocity fields.
4. Practical Applications: The sections also include practical examples where problems regarding material accelerations are solved using specific velocity fields.
Overall, the application of these principles is crucial in analyzing and predicting fluid motion and behaviors.
Youtube Videos

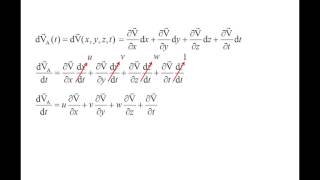







![Material derivative [Fluid Mechanics #3a]](https://img.youtube.com/vi/dIGMArhv7Fc/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Material Derivative
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The material derivative: \[ \frac{D}{Dt} = \frac{\partial}{\partial t} + \mathbf{V} \cdot \nabla \]
Detailed Explanation
The material derivative is a way to describe how a quantity, such as velocity or pressure, changes for a moving fluid particle over time. It combines both the local time change (indicated by the partial derivative) and the change due to motion through space (this is captured by the convective term represented as \( \mathbf{V} \cdot \nabla \)). Essentially, it accounts for how the properties of the fluid are experienced by an observer moving along with it.
Examples & Analogies
Imagine you're traveling in a car. As you're driving down the road, you're not just seeing the scenery change in front of you (which relates to the convective part), but you're also experiencing changes in temperature as you enter different weather zones. The material derivative is like keeping track of all these changes you experience because you're moving.
Local and Convective Acceleration
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This component, called local acceleration, refers to changes in velocity due to local changes over time at a point. Convective acceleration arises due to spatial changes in velocity as the fluid particle moves.
Detailed Explanation
Local acceleration is when the velocity of a fluid particle changes because of alterations at the same location over time. In contrast, convective acceleration happens because a fluid particle moves through a velocity field that varies from place to place. Understanding both components is crucial for analyzing fluid flow behaviors.
Examples & Analogies
Consider a river current. If you stand on a bridge (local acceleration), and you notice the water speed changing at that spot due to an incoming storm, that's local acceleration. Meanwhile, if you were to float down the river and notice that certain sections are faster than others (like rapids), that would be convective acceleration.
Material Derivative of Pressure and Density
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If my particles having the density as I earlier say that particles can have the density, my virtual fluid balls can have a different density, if I define that I can define with a material derivative of the density.
Detailed Explanation
The material derivatives for pressure and density are similar concepts to that of velocity. They show how these quantities change as you move along with a fluid particle. By establishing a material derivative for these variables, we can analyze how density and pressure change under different conditions in the fluid, which is essential for solving hydrodynamic problems.
Examples & Analogies
Think about how the pressure feels when you're swimming at varying depths in a pool. As you dive deeper, the pressure increases; if you're moving a buoyant ball of varying density through different layers of water, the way that pressure changes along with the ball as it moves represents the material derivative of pressure and density.
Application in Fluid Mechanics
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We can compute the accelerations field, we can compute this material derivative of the pressures, we can compute the material derivative of density with the same format.
Detailed Explanation
In fluid mechanics, applying the material derivative allows us to compute how pressures and densities change in a fluid flow. This capability is vital for predicting behavior in various scenarios like weather patterns, ocean currents, or aerodynamics. With these calculations, engineers and scientists can model and simulate physical phenomena effectively.
Examples & Analogies
Consider a weather balloon rising through the atmosphere. As it rises, the pressure and density conditions change continuously due to its upward motion. Applying material derivatives helps us understand and calculate how the weather balloon's ascent affects the measurements taken by the sensors onboard.
Key Concepts
-
Material Derivative: A concept essential for analyzing changes in fluid properties along with moving particles.
-
Local and Convective Acceleration: The two components contributing to changes in velocity experienced by fluid particles.
-
Application in Fluid Dynamics: Material derivatives are used to model and predict fluid behaviors like flow stability and pressure variations.
Examples & Applications
The material derivative of a density can be calculated using the formula involving local time derivatives and convective changes.
In fluid flow through an inclined pipe, using material derivatives helps calculate how pressure changes along the pipe due to varying velocity.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Material derivative, a fluid's best friend, it tracks change as the particles wend.
Stories
Imagine a fluid droplet flowing downstream; the material derivative tells its tale of how density and pressure shift along its journey.
Memory Tools
Remember the acronym 'L and C' for Local and Convective changes in fluid behavior!
Acronyms
Use 'P.V.A.' for Pressure, Velocity, Acceleration when calculating material derivatives.
Flash Cards
Glossary
- Material Derivative
The total derivative of a quantity that accounts for changes due to both local time variation and spatial movement.
- Local Acceleration
The change in velocity at a fixed point in time.
- Convective Acceleration
The change in velocity experienced by a fluid particle as it moves through space.
- Velocity Field
A function that assigns a velocity vector to every point in space.
- Acceleration Field
A description of how acceleration varies across different points in a fluid.
Reference links
Supplementary resources to enhance your learning experience.
