Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Velocity in Fluid Dynamics
Unlock Audio Lesson
Today we will start with the fundamental concept of velocity in fluid dynamics, focusing on radial and tangential velocities. Can anyone define what we mean by radial velocity?
Radial velocity is the component of the velocity that moves outward from a central point.
Great job! Radial velocity describes movement away from a point. And tangential velocity refers to?
Tangential velocity is the velocity along the path of motion, perpendicular to the radius.
Exactly! Remember that tangential velocity is crucial for circular motions and understanding how fluids behave at different points in a system. Let’s move on to velocity distributions in nozzles.
Acceleration in the X-Direction
Unlock Audio Lesson
We discussed velocities, now let’s focus on acceleration in the x-direction. Who can explain the relationship between acceleration and velocity?
Acceleration is the derivative of velocity over time, right?
Correct! Now in our scenario of steady flow, how do we simplify this?
We can ignore the time component if there’s no change over time, making it easier to calculate.
Exactly! So in steady flow, we can conclude numerous components become zero. And hence, the acceleration calculations simplify significantly.
Applying Velocity Concepts
Unlock Audio Lesson
Let’s apply what we’ve learned. Consider a converging nozzle. If we have an initial velocity at the entrance, how do we calculate the velocity at the exit?
We can use the principle of conservation of mass or Bernoulli’s equation!
Exactly! And what information do we need?
We need the inlet velocity and the nozzle dimensions.
Perfect! Once we have that, we can also compute the acceleration using the velocity differences at the two points.
Overview of Practical Applications
Unlock Audio Lesson
To summarize our discussions, can anyone share how understanding radial and tangential velocities might apply in real-world situations?
In many engineering applications like jet engines and water jets, knowing these velocities helps in building efficient systems.
Exactly! It’s crucial in designing nozzles and optimizing flow rates. Keep these concepts in mind as they are key to many areas in fluid dynamics.
I can see how this ties into more complex systems we’ll study later!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the definitions and calculations of radial and tangential velocities in fluid dynamics. It emphasizes the relationship between velocity distribution and the acceleration components in one-dimensional flows, particularly through nozzles, and describes how to derive and interpret these velocities in various contexts, including steady flows and two-dimensional patterns.
Detailed
Radial and Tangential Velocities
In this section, we investigate two critical aspects of fluid motion: radial and tangential velocities. These velocities are essential in understanding fluid behavior in various scenarios, particularly in nozzle flows where fluid dynamics can significantly impact performance.
Key Concepts:
- Velocity Distributions: The velocity field is defined with respect to the x-direction and varies with the fluid's entrance and exit points. We explore basic equations governing these distributions, helping to formulate a pathway for analyzing acceleration in fluid motion.
- Acceleration in x-Direction: We derive expressions for acceleration along the x-direction using total derivatives and demonstrate how these quantities relate to velocity distributions within a nozzle. Through mathematical manipulation, we conclude that, for steady-state flow in one-dimension, the acceleration can be simplified.
- Application and Examples: The section discusses examples where these concepts apply, such as determining the velocity increase across a converging nozzle, thus tying theoretical calculations to practical scenarios encountered in fluid mechanics.
In summary, the section lays a robust foundation for understanding how velocity influences acceleration in fluid flows, paving the way for further explorations in fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
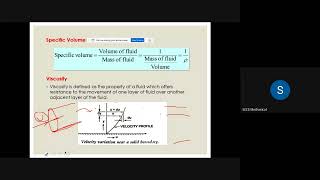
Understanding Velocity Distributions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And the velocity distributions is given with respect to the x directions this is about the nozzles. The velocity field is given as the
2π√(A/(π ⋅ ρ)) u1 ∈ 1
This is what the velocity distributions given to us.
Detailed Explanation
In fluid dynamics, velocity distributions define how fluid speed varies across different points in a flow field. In this case, we're considering flow through a nozzle. The specific terms and formulas indicate the variation of velocity in relation to the x-direction, which is critical in analyzing how fluids behave as they move through constrictions like nozzles. The formula mentioned is a mathematical representation of velocity at specific points within this system.
Examples & Analogies
Imagine a garden hose; when you place your thumb partially over the end, the water speed increases as it exits the smaller opening. Here, the nozzle works similarly by constricting flow, causing the velocity of the fluid to increase, which is represented mathematically in the velocity distribution.
Calculating Acceleration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What we have to need to compute it? What is the acceleration in the x directions? du/dt at the entrance point at this x = 0 that is what the entrance and this is what of exit of the flow.
Detailed Explanation
To find the acceleration of the fluid in the x-direction, we look at how the velocity changes with respect to time. This is represented by the term du/dt, where 'u' is the velocity and 't' is time. By evaluating this at specific points, such as the entrance and exit of the nozzle (at x = 0 and x = L), we can determine how rapidly the fluid accelerates through the nozzle.
Examples & Analogies
Consider riding a bike down a hill: at the top (entrance), you're moving slower and as you reach the bottom (exit), you speed up. The change in your speed over time as you descend the hill is akin to the acceleration of fluid through the nozzle.
Characterizing 1-Dimensional Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
I am just highlighting it this is the what 1 dimensional flow only x directions component what we have. That means the by definitions the accelerations and along the x directions accelerations the accelerations in the x directions can be written as very simple forms just taking the definitions that the accelerations will be total derivative of du/dt.
Detailed Explanation
1-dimensional flow implies that fluid movement can be effectively analyzed in just one direction. This simplifies our calculations since we only need to consider changes in velocity along the x-axis. The acceleration in this case can be expressed mathematically, indicating both local and convective components, making it easier to understand how fluid behaves under different conditions.
Examples & Analogies
Think of a straight slide in a water park. The water flows down the slide in a single direction (1-dimensional flow), making it easy to predict how fast the water will move and where it will land at the bottom.
Substituting Values for Calculating Accelerations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you just substitute this value and do a partial derivative of this u with respect to x and if you substitute it will get it the du that by substitute it is
(Using formulas with specific values),
So it is very easy as you do a partial derivative with respect to x.
Detailed Explanation
By substituting specific values into our formulas and performing mathematical operations, we can numerically determine the acceleration. The partial derivative of the velocity with respect to x provides insights into how changes in position (x) affect fluid acceleration. This is essential in providing precise predictions of fluid behavior within the nozzle.
Examples & Analogies
Imagine taking measurements on a curve. If you measure your height at different points along the curve, you could determine how steep it is getting. Similarly, by substituting values for position (x) in our calculations, we precisely understand the acceleration of the fluid at various positions in the nozzle.
Final Calculations at Entrance and Exit Points
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So using given data we can compute it the accelerations in the x directions du/dt at x = 0.
When x = 0, the value substituting the V and the L value gives 200 feet per second square. At exit point where x = L just substituting here, x = L results in du/dt = 600 feet per second squared.
Detailed Explanation
By applying the defined formulas for acceleration at specific points, we calculate the accelerations at the entrance (x=0) and exit (x=L) of the nozzle. These values help illustrate how fluid accelerates as it moves through the nozzle, showcasing the increase from 200 ft/s² at the entrance to 600 ft/s² at the exit.
Examples & Analogies
Think of a car accelerating down a highway. As it merges into faster traffic from a stop (entrance), it might initially go 20 mph and then reach 60 mph as it steps on the gas to keep up with the flow of fast vehicles on the road (exit).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Velocity Distributions: The velocity field is defined with respect to the x-direction and varies with the fluid's entrance and exit points. We explore basic equations governing these distributions, helping to formulate a pathway for analyzing acceleration in fluid motion.
-
Acceleration in x-Direction: We derive expressions for acceleration along the x-direction using total derivatives and demonstrate how these quantities relate to velocity distributions within a nozzle. Through mathematical manipulation, we conclude that, for steady-state flow in one-dimension, the acceleration can be simplified.
-
Application and Examples: The section discusses examples where these concepts apply, such as determining the velocity increase across a converging nozzle, thus tying theoretical calculations to practical scenarios encountered in fluid mechanics.
-
In summary, the section lays a robust foundation for understanding how velocity influences acceleration in fluid flows, paving the way for further explorations in fluid dynamics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a converging nozzle, the velocity of a fluid increases as the cross-sectional area decreases, illustrating the conservation of mass.
-
To calculate acceleration at the exit of a nozzle, one can derive it from changes in velocity as the fluid flows through.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Radial moves away, tangential goes around, fluid flows in motion, watch how it’s found!
📖 Fascinating Stories
-
Once there was a fluid named Rad who loved to move outward from the center, while his friend Tang liked to spin around at the edges! They would play in the nozzle, where Rad would speed up as he narrowed, while Tang enjoyed his merry-go-round.
🧠 Other Memory Gems
-
RAT - Radial means Away from center, Tangential means Along the path.
🎯 Super Acronyms
RVT - Remember Velocity Types
- Radial
- Velocity is Tangential.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Radial Velocity
Definition:
The component of velocity that points outward from a specific center point.
-
Term: Tangential Velocity
Definition:
The velocity component that moves parallel to the motion's path, perpendicular to the radius.
-
Term: Velocity Distribution
Definition:
The variation of fluid velocity within a specific field or region.
-
Term: Acceleration
Definition:
The rate of change of velocity with respect to time.
-
Term: Steady Flow
Definition:
A flow condition where the fluid properties at a point do not change with time.
-
Term: Nozzle
Definition:
A device designed to control the direction or characteristics of fluid flow as it exits an enclosed chamber.