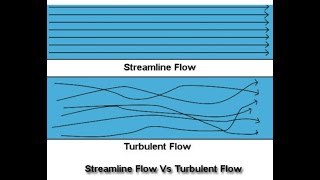
12.4.2. Sketching of Streamlines

The velocity distributions is given with respect to the x directions this is the about the nozzles. The velocity field is given as the $V = 2\sqrt{y} - \frac{4}{3}$ which indicates how velocity varies in x direction with respect to the nozzle geometry. At the entrance, we consider the velocity and the conditions to compute acceleration in the x direction, $du/dt$.

This chunk introduces the concept of velocity distributions, particularly how they vary in a nozzle. Here, the velocity field's equation shows how the flow changes with the nozzle's geometry. It emphasizes the need to calculate accelerations at specific flow points where the fluid enters the nozzle, which is crucial for understanding the nozzle dynamics.

Think of running water through a garden hose: as you pinch the end of the hose, the velocity increases because the water is forced through a smaller opening. This illustrates how a nozzle's geometry affects water speed.

We need to compute accelerations in the x direction, $a_x = \frac{du}{dt}$, particularly at entrance and exit points. If the velocity at the entrance is 10 ft/s and the length is 1 ft, we find these accelerations as derivatives of the flow velocity with respect to time.

This chunk delves deeper into calculating the acceleration in fluid flow. The acceleration component is defined as how velocity changes over time. By analyzing the velocity at specific points (the entrance and exit of the nozzle), we can evaluate how quickly the flow speed is changing, which is essential for predicting flow behavior in the nozzle.

Consider a car accelerating: if the driver presses the gas pedal, the speed of the car increases over time. Similarly, in fluid dynamics, if the fluid's velocity increases as it flows through a nozzle, that change in speed represents acceleration.

The acceleration in the x direction can also be computed using the total derivative of the velocity component with respect to time, expressed as a partial derivative to account for steady flow conditions.

Here, we focus on the mathematical aspect of calculating flow acceleration using partial derivatives. This is important in steady flow, where the velocity does not change over time, meaning that we can simplify some components of our calculations. The chunk explains that under certain conditions (steady and one-dimensional flow), the time derivatives can be considered zero, simplifying the process significantly.

Picture a train moving steadily along a track; if no external forces act on it, its speed remains constant despite time passing. In fluid dynamics, when conditions are stable, we can disregard any time-related changes in velocity.

After substituting values for velocity and length into our equations, we find the accelerations at the entrance point and exit point. The result shows that the acceleration increases in the flow direction.

This segment summarizes the results of our calculations. By substituting specific flow values into the equations derived earlier, we can determine real acceleration values at both the entrance and the exit of the nozzle. This highlights how acceleration changes from the start to the end of the flow path, demonstrating the physical behavior of the fluid within the system.

Like a roller coaster that accelerates down a slope, the nozzle also shows how fluid accelerates due to the pressure and geometry. At the beginning, the flow has one speed, but as it pushes through the constriction of the nozzle, it speeds up, similar to a coaster gaining speed when descending from a height.

--