Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Velocity Distribution in Nozzles
Unlock Audio Lesson
Today, we're learning about the velocity conditions in nozzles. Can anyone tell me why understanding velocity distributions is important in fluid dynamics?
I think it helps us design systems that regulate or direct fluid flow better?
Exactly! By analyzing velocity at different points in a nozzle, we can predict flow behavior and optimize designs. The formula we often encounter is V_exit = 3 * V_entrance, showing how exit velocity relates to entrance velocity.
How do we calculate acceleration in this context?
Great question! The acceleration in the x-direction can be determined through the total time derivative of the velocity component along x. Let's remember: 'A = ∂u/∂t + u * ∂u/∂x'. In steady flows, some components can simplify to zero.
So, if we're dealing with a steady flow, we mostly look at changes in velocity instead?
That's correct! If we take a steady flow, the acceleration primarily depends on the spatial change in velocity. Remember, local changes are crucial!
Could you summarize the key points we covered?
Of course! We discussed that the exit velocity in nozzles is typically greater than the entrance velocity, calculated as three times in our example. We defined acceleration in the x-direction through derivatives and simplified under steady flow conditions, focusing on spatial velocity changes.
Calculating Accelerations in Nozzles
Unlock Audio Lesson
Now, let's focus on calculating acceleration. Can anyone tell me what equations we use for calculating acceleration in a nozzle?
We use the total derivative of velocity, which breaks down into local and convective acceleration components!
Exactly! We can simplify our calculations significantly for steady, one-dimensional flow. Let's revisit how we compute acceleration. We typically set ∂u/∂t = 0 in our steady-state scenario.
So the focus is primarily on ∂u/∂x, right?
That's right! As you all mentioned, it becomes vital when the flow remains steady. When we calculate acceleration at specific points like the entrance or exit, the given data becomes crucial, such as the entrance velocity being 10 ft/s in our example.
If V at entrance is 10 ft/s, then at exit, it would be 30 ft/s or so?
Exactly! And those values allow us to determine acceleration. Any thoughts on the significance of this information?
I guess it helps us predict how the fluid will behave in a nozzle!
Exactly right! In summary, we discussed the importance of calculating acceleration through changes in velocity, focusing on local acceleration components in steady flow. Keep this in mind when working through real problems.
Practical Application of Nozzle Conditions
Unlock Audio Lesson
Now let's connect our theoretical understanding to practical applications. Why do engineers need to know about these velocity conditions in nozzles?
To design effective fluid systems, right? Like engines or piping systems?
Precisely! Engineers utilize these principles to enhance flow efficiency, reduce backflow, and design efficient nozzles. Understanding how velocity changes can drastically affect performance is vital.
Are there real-world examples of this?
Absolutely! In jet engines, for instance, the design of nozzles maximizes the jet velocity to produce thrust. As you can see, every aspect learned here has practical implications. Can someone summarize the importance of these equations?
They help engineers design systems that optimize flow to improve performance in various applications.
Great summary! Remember, understanding the principles behind velocity conditions allows for innovative designs in fluid mechanics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the velocity distribution in nozzles and how to calculate the acceleration in the x-direction. We analyze how changes in velocity from the entrance to the exit of a nozzle reflect on the acceleration, emphasizing the relationship between fluid dynamics and nozzle design.
Detailed
In this section, we delve into the concept of velocity conditions within nozzles, emphasizing the relationship between velocity distributions and accelerations. Starting with the basic principles, we define the velocity field based on given relationships, such as velocity at the entrance and exit points. The discussion includes the acceleration in the x-direction defined as the total time derivative of velocity, incorporating local and convective acceleration components. Key formulas and calculations showcase how to derive accelerations based on given flow conditions, assessing both entrance and exit scenarios in a simplified manner. This foundational knowledge aids in understanding the impact of nozzle design on fluid acceleration and velocity, paving the way for practical applications in fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Velocity Distribution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
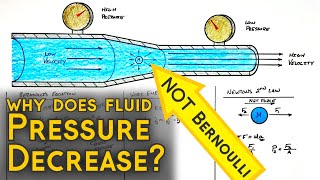
And at the entrance points and the velocity at the exit point will be the 3. And the velocity distributions is given with respect to the x directions this is about the nozzles. The velocity field is given as the 2.
Detailed Explanation
This part introduces the concept of velocity distribution in a nozzle. The velocity at the entrance and exit points is essential to understanding how the flow behaves. The velocity distribution is mentioned to change along the x-direction as it moves through the nozzle. We will soon define how to calculate this distribution mathematically.
Examples & Analogies
Imagine a garden hose. When you cover part of the nozzle with your finger, the water shoots out faster. Here, the nozzle's entrance can be compared to your finger covering the hose, making the flow velocity change from entry to exit.
Acceleration Calculation Concepts
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What we have to need to compute it? What is the acceleration in the x directions? du/dt at the entrance point at this x = 0 that is what the entrance and this is what of exit of the flow.
Detailed Explanation
To understand fluid acceleration, we need to compute the change in velocity (du) with respect to time (dt) at different points, particularly at the nozzle's entrance and exit. This calculation is crucial for analyzing how fast the flow accelerates through the nozzle.
Examples & Analogies
Think of a car at a traffic light. When the light turns green, the acceleration from a stop is essentially what we're measuring at that moment, similar to measuring how quickly the water accelerates at the entrance of the nozzle.
Deriving Acceleration in Nozzles
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if it is the conditions we need to compute it what will be the accelerations ax du/dt. If the ... this value what will be the acceleration at the entrance point and the exit point. This is one of the easiest problems.
Detailed Explanation
This chunk elaborates on how to derive the acceleration (ax) using the fundamental principles of fluid dynamics. It discusses the total derivative of the velocity component, focusing on the relevant parameters that influence acceleration as the fluid moves from the entrance to the exit of the nozzle.
Examples & Analogies
Consider a downhill slide. As you start sliding at the top, your acceleration increases as you go down. Similarly, in the nozzle, as the fluid travels from a wider entrance to a narrower exit, its acceleration increases.
Impact of Steady Flow Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But if you look at these problems what are the components can be neglected as it is a steady flow there is no time component on this. We can make it this equal to 0.
Detailed Explanation
In a steady flow, certain components can be neglected, which simplifies the overall analysis. The absence of time-dependent changes means that the acceleration terms can be treated as zero for calculations, allowing us to focus only on the spatial variations in velocity.
Examples & Analogies
Think about a train cruising on a straight track versus when it is accelerating or decelerating. While cruising (steady flow), the speed remains unchanged; thus, we can ignore changes as long as we look at a specific segment of the journey.
Extracting Velocity at Specific Points
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So it is quite easy we have to compute this part. So if you just substitute this value and do a partial derivative of this u with respect to x and if you substitute it will get it the du...
Detailed Explanation
This section discusses how to compute the velocity at specific points in the nozzle using partial derivatives. When substituting specific values for x, we can derive the relationship between velocity and the changes observed in the nozzle, leading us to understand how it varies across different sections.
Examples & Analogies
Imagine a baking process where you check the temperature of cookies at different points in the oven. By recording each temperature change, you can analyze how evenly the cookies are baked based on their specific oven location.
Calculating Accelerations at Entrance and Exit Points
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we know this how this accelerations ax varies with respect to x and what is a functions in terms of V and the L? ... exit point where x = L just substituting here, x = L value.
Detailed Explanation
Finally, we calculate the accelerations at both the entrance and exit points of the nozzle by substituting the known values for velocity (V) and the length (L). This gives us specific acceleration values at the starting and ending points of flow through the nozzle.
Examples & Analogies
Consider a water slide where you enter slowly at the top (entrance point) but exit quickly at the bottom (exit point). The change in your speed represents the acceleration calculated at these points.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Velocity Conditions: Key to understanding fluid behavior in nozzles.
-
Acceleration Calculations: Necessary for predicting fluid behavior under varying velocity conditions.
-
Steady Flow Assumptions: Simplify calculations in practical scenarios.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A nozzle with an entrance velocity of 10 ft/s and an exit velocity of 30 ft/s illustrates how velocity changes impact acceleration.
-
The application of these principles is crucial in the design of jet engines where optimized nozzle design maximizes thrust.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When a nozzle's mouth gets slim, velocity goes up on a whim!
📖 Fascinating Stories
-
Imagine a water slide; as the slide narrows, kids fly out faster at the exit due to increased flow.
🧠 Other Memory Gems
-
A = Changin' in U, through time and space, watch it accelerate in the nozzle's race!
🎯 Super Acronyms
V.E.N.T. - Velocity Exits Next Through, captures how fluid flows through nozzles.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Velocity
Definition:
The speed of something in a given direction.
-
Term: Acceleration
Definition:
The rate of change of velocity per unit of time.
-
Term: Local Acceleration
Definition:
Acceleration due to changes in velocity with respect to time at a specific point.
-
Term: Convective Acceleration
Definition:
Acceleration due to the movement of a fluid parcel as it moves through a velocity gradient.