Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Continuum Hypothesis
Unlock Audio Lesson
Today we'll discuss the continuum hypothesis, a critical assumption in fluid mechanics. Can anyone explain what this hypothesis entails?
Is it about treating fluids as continuous rather than discrete?
Exactly! The continuum hypothesis simplifies the analysis by ignoring the molecular structure of fluids, allowing us to view them as continuous matter. This concept is vital when deriving equations like the Cauchy and Navier-Stokes equations. Remember, fluids behave differently at the molecular level compared to the continuum level.
So, how does this apply when we talk about stress in fluids?
Great question! Stress in fluids arises from internal resistance forces per unit area. In a continuum model, we treat these stresses using tensors, which helps us describe how fluids resist deformation.
Deriving Cauchy's Equation
Unlock Audio Lesson
Now, let’s derive Cauchy's equations. Can anyone tell me which assumptions we need?
Do we need to consider the continuity of the fluid elements?
Absolutely! Continuity is essential. It allows us to apply differential calculus, using Taylor series to describe how fluid properties change over space and time.
And what do we mean by tensor stress components in this context?
Tensor stress components represent how internal forces act within the fluid. They help us translate momentum changes into forces acting on control volumes, essential for formulating these equations.
So, every time we derive these equations, we’re relying on these foundational assumptions?
Correct! Understanding these assumptions guides us to apply computational methods effectively.
Application in Computational Fluid Dynamics
Unlock Audio Lesson
Let's connect these assumptions to computational fluid dynamics. How do you think assumptions guide the simulations?
They simplify the modeling, making it computationally feasible, right?
Exactly! By relying on the continuum hypothesis and stress tensors, we can model complex flows, such as around a bridge pier, without getting caught up in immense computational demands.
Are there limitations to these assumptions in simulations?
Absolutely! The assumptions may neglect certain microscopic effects, which might be significant in cases of very low viscous flows or at small scales. Always consider the context of the problem!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section illustrates crucial assumptions in fluid mechanics supporting the development of Navier-Stokes equations through an understanding of linear momentum equations. It highlights the significance of mathematical interpretation along with the application of computational fluid dynamics in solving complex fluid flow problems.
Detailed
Assumptions in Fluid Mechanics
In fluid mechanics, some fundamental assumptions allow for the simplification of fluid motion into manageable equations, such as the Cauchy and Navier-Stokes equations. This section highlights these assumptions, including the continuum hypothesis, which implies treating fluids as continuous media. Moreover, defining the relevant stress tensors enables us to understand internal forces acting per unit area within a fluid. These principles ultimately facilitate the numerical simulation of fluid movements, crucial in computational fluid dynamics applications, particularly in addressing complex real-life problems like fluid flows around structures.
Youtube Videos
![Common assumptions in fluid mechanics [Fluid Mechanics #3b]](https://img.youtube.com/vi/kimMbNP9DrY/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We look at how fluid particles move through space and time, considering their velocity, pressure, and density as functions of these variables. This understanding is crucial in the study of fluid dynamics.
Detailed Explanation
Fluid flow is analyzed by observing how the properties of fluids, such as velocity, pressure, and density, change over time and different locations in space. Fluids are treated as continuous substances, allowing us to apply mathematical techniques to describe their behavior efficiently. Understanding these changes is essential for predicting how fluids behave in various scenarios, such as in pipes or around objects.
Examples & Analogies
Imagine watching a river flow. As you stand at different points along the river, you notice that the speed of the water changes depending on the landscape. In some areas, it rushes rapidly over rocks; in others, it flows gently. Just like the river, fluids in engineering systems behave differently based on their velocity, pressure, and density as they interact with their surroundings.
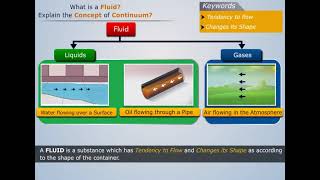
The Continuum Hypothesis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The continuum hypothesis assumes that fluid properties are continuously distributed throughout the material, allowing us to treat fluids as if they are made up of infinitely small particles.
Detailed Explanation
The continuum hypothesis simplifies fluid mechanics by assuming that properties like temperature, pressure, and density change smoothly and continuously within a fluid body. This means we can model fluids as continuous materials rather than discrete particles. This assumption is critical for deriving equations like the Navier-Stokes equations, which describe how fluids move.
Examples & Analogies
Think of a sponge soaked with water. While the individual water molecules are discrete, the sponge appears to contain a smooth and uniform height of water. This uniformity holds true enough that we can treat the water as a continuous fluid despite its made-up molecules.
Trace and Stress Tensors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In fluid mechanics, we also discuss trace tensors, which help us understand how stress is distributed within a fluid.
Detailed Explanation
Stress in fluid mechanics refers to the internal resistance a fluid encounters when it deforms. Stress tensors provide a mathematical framework to quantify this resistance, showing how forces are distributed across different directions within the fluid. Understanding trace and stress tensors is essential for predicting how fluids behave under various forces and conditions.
Examples & Analogies
Imagine squeezing a balloon. As you apply pressure, the surface of the balloon experiences stress in various directions. The balloon's smooth surface distributes that stress throughout, which is akin to how fluids handle internal forces. The balloon's ability to stretch and deform reflects the concepts of stress and trace tensors in fluid mechanics.
Momentum and Mass Flux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We must also consider the mass flux and momentum in fluid flow, which involve analyzing the rates at which mass and momentum transfer through a control volume.
Detailed Explanation
Mass flux refers to the mass of fluid passing through a unit area over a specific time, while momentum flux relates to how momentum (mass times velocity) changes within the fluid flow. These concepts are essential for understanding how fluids will behave in different conditions, especially in engineering applications such as pipe flow and aerodynamics. The equations derived from these concepts help to analyze and predict fluid movements.
Examples & Analogies
Picture a team of soccer players moving towards a goal. The number of players (mass flux) flowing through the goal line directly relates to how they might impact the game's outcome (momentum flux). If many players rush through quickly, they generate substantial momentum towards scoring. This analogy illustrates the flow of fluids in practical terms, showing how we can predict outcomes based on the mass and momentum transfer.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Continuum Hypothesis: Allows the treatment of fluids as continuous, ignoring molecular details to simplify analysis.
-
Stress Tensor: Represents internal resistance forces within the fluid, crucial for understanding fluid behavior.
-
Cauchy's Equation: Forms the basis for deriving other complex fluid motion equations critical in computational fluid dynamics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Utilizing conceptual models of fluid flow around structures to demonstrate velocity and pressure changes.
-
Applying the continuum hypothesis to predict fluid behavior in channels without considering molecular interactions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When fluids flow, it's good to know, Treat them continuous, let that be the show!
📖 Fascinating Stories
-
Imagine a river, smooth and wide, we don't see the atoms inside. Just like how we flow, these concepts go, in fluid dynamics, assumptions help us know!
🧠 Other Memory Gems
-
Continuous assumption: C for continuity, A for assumptions, T for tensors, makes fluid motion a breeze!
🎯 Super Acronyms
CATS - Continuum assumption, Assumptions about Tensor Stress.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Continuum Hypothesis
Definition:
Assumption in fluid mechanics stating that fluids can be considered continuous, ignoring molecular structure.
-
Term: Cauchy's Equation
Definition:
Fundamental equation in fluid mechanics concerning the state of motion of fluid particles in a continuum.
-
Term: Stress Tensor
Definition:
Mathematical representation of internal resistance forces per unit area within a fluid.
-
Term: NavierStokes Equations
Definition:
Equations that describe the motion of fluid substances, built on the principles of motion and conservation.