Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Mechanics
Unlock Audio Lesson
Good morning, everyone! Today, we will begin our journey into fluid mechanics by discussing the Navier-Stokes equations, a cornerstone of this field. What do you think these equations describe?
They describe the motion of fluids, right?
Exactly! The Navier-Stokes equations model how fluids behave under various forces. They are derived from the principles of linear momentum. Can anyone tell me what linear momentum is?
It's the product of mass and velocity?
Yes! And in fluid mechanics, we also consider the mass density and the effects of pressure. Another fundamental aspect we will look into today is Cauchy's equations, which precede the Navier-Stokes equations. Remember our mnemonic 'C-M-P'? It stands for Continuum, Momentum, and Pressure - key elements in understanding fluid dynamics.
What are Cauchy's equations about again?
Cauchy's equations summarize the relationship between stresses within a moving fluid and the conditions affecting its motion.
So, they are like a stepping stone to understand Navier-Stokes?
Precisely! Cauchy's equations give us the framework for the stress at every point in the fluid, which we will incorporate into our Navier-Stokes model.
In summary, we've covered that the Navier-Stokes equations are derived from the concept of linear momentum and that Cauchy's equations are foundational to understand these concepts.
Cauchy's Equations and Stress Tensors
Unlock Audio Lesson
Now, let's discuss Cauchy's equations in detail. Can anyone explain how stress is defined in fluid mechanics?
It's the internal resistance force per unit area, right?
Correct! Stress tensors help us understand how fluids deform under shear. Does anyone remember how we denote stress tensors?
They use two subscripts to indicate the plane and the direction the stress is acting, like σ_xx or σ_xy?
Good job! Each component of the stress tensor tells us how forces behave on different planes within the fluid. Let's summarize that: stress tensors are fundamental to describing how fluid substances interact under various forces.
Why are these equations so important in computational fluid dynamics?
The Navier-Stokes equations, which incorporate these stress tensors, allow us to simulate and solve complex fluid flow problems effectively, from environmental issues to engineering designs.
So far, we have focused on the role of stress defined by Cauchy's equations. We now appreciate how it leads us to the Navier-Stokes equations.
Derivation of Navier-Stokes Equations
Unlock Audio Lesson
Let’s move to the derivation of the Navier-Stokes equations. What is the basic principle behind these equations?
They are based on Newton's second law applied to fluid motion.
Exactly! We apply Newton's second law to a small control volume in the fluid. We'll be accounting for body forces and surface forces acting on this volume. Can anyone think of examples of these forces?
Gravity is a body force, right? And pressure forces can be surface forces?
Spot on! We quantify forces per unit volume. Now considering the continuum hypothesis, which assumes a fluid is continuous and incompressible, let’s derive the equations. We'll utilize Cauchy's equations, focusing on the conservation of momentum. Remember, we can simplify this using Taylor series to understand the variations within the control volume.
What does this lead to in terms of the equations?
We can arrive at three distinct equations for the x, y, and z momentum, which will ultimately form our Navier-Stokes equations.
In summary, we've discussed that the Navier-Stokes equations originate from Newton's laws, are affected by body forces and surface forces, and require understanding of stress tensors and the continuum hypothesis.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section provides a thorough derivation of the Navier-Stokes equations, which are essential for understanding fluid dynamics in computational fluid dynamics. It introduces Cauchy's equations as foundational to the Navier-Stokes equations.
Detailed
Detailed Summary
The Navier-Stokes equations are pivotal in fluid mechanics, representing the behavior of viscous fluid flow. They comprise a set of nonlinear partial differential equations derived from Newton's second law applied to fluid motion, accounting for velocity, pressure, density, and external forces. This section outlines the fundamental components leading to the derivation of the Navier-Stokes equations by first exploring Cauchy's equations which lay the groundwork for the differential formulation of fluid dynamics. Key concepts include the definition of velocity fields, pressure fields, body forces, and surface forces acting on control volumes. The significance of the continuum hypothesis and stress tensors is also highlighted, forming the backbone of understanding in computational fluid dynamics. An emphasis is placed on practical applications of these equations in simulating real-world fluid flow scenarios, such as environmental engineering and structural analysis.
Youtube Videos
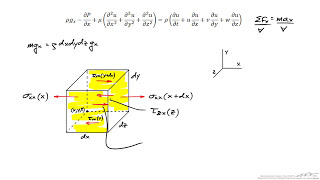
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Before deriving the Navier-Stokes equations, we are going to derive Cauchy equations, which are very important equations when you go for differential form of linear momentum equations.
Detailed Explanation
This chunk introduces the Navier-Stokes equations and emphasizes their importance in fluid mechanics. Before these can be understood, it is essential to grasp the foundational Cauchy equations, which apply to linear momentum in fluid flow.
Examples & Analogies
Consider a river flowing steadily. The Navier-Stokes equations allow us to model and predict how the water will flow around obstacles (like rocks), while the Cauchy equations help to understand the fundamental forces acting on that water.
Complexity of the Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Mathematically, this chapter looks very complex, but I will try to deliver this lecture as simply as possible without going into too much detail about mathematics.
Detailed Explanation
The author acknowledges that although the Navier-Stokes equations can seem complicated due to their mathematical structure, the goal is to present this material in a clear and understandable manner. Emphasizing clarity over mathematical complexity helps students grasp the underlying principles without becoming lost in formulas.
Examples & Analogies
Think about learning to swim versus mastering swimming techniques. Initially, it may seem overwhelming, but once you start practicing the basics, you can begin to understand the movements required without needing to know all the technical jargon of swimming competitions.
Understanding Computational Fluid Dynamics (CFD)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We follow the book of Sinzel Simbala, which provides interesting derivations and illustrations that help in understanding fluid mechanics problems.
Detailed Explanation
This chunk highlights the importance of educational resources like textbooks in mastering complex topics. The material emphasizes how visual aids and well-explained derivations can significantly aid understanding of fluid dynamics, particularly computational simulations used in solving practical problems.
Examples & Analogies
Just like a recipe book can simplify cooking complicated dishes through step-by-step instructions and pictures, a good textbook can demystify fluid dynamics, making it easier for students to comprehend challenging concepts.
Applications of CFD
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Today, we have used CFD software called Flow 3Ds to solve basic problems related to velocity field, pressure, and density.
Detailed Explanation
This chunk discusses practical applications of Computational Fluid Dynamics (CFD) in solving real-world problems. By using software like Flow 3Ds, students can visualize how fluid flows under various conditions, looking at critical factors such as velocity, pressure, and density.
Examples & Analogies
Imagine using a flight simulator to understand how the airplane responds to weather changes in the air. CFD software operates similarly, allowing engineers to predict how fluids interact in different environments without needing to conduct extensive physical experiments.
Understanding the Navier-Stokes Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Navier-Stokes equations look like nonlinear partial differential equations which involve variables like velocity (u, v, w), pressure, and density.
Detailed Explanation
In this section, the Navier-Stokes equations are described as nonlinear partial differential equations that incorporate various physical quantities involved in fluid dynamics, including velocity, pressure, and density. This complexity arises from the interactions between these parameters and how they change over time and space.
Examples & Analogies
Think of a busy highway. The traffic flow (analogous to fluid flow) is influenced by various factors like speed limits (pressure), vehicle sizes (density), and driving habits (velocity variations). The Navier-Stokes equations help us understand how these factors interact to form the flow's overall pattern.
Deriving the Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We can derive the Navier-Stokes equations step by step using the hypothesis of continuum, meaning we can treat the fluid as a continuous medium.
Detailed Explanation
This chunk covers the method of deriving the Navier-Stokes equations, which involves the continuum hypothesis. This hypothesis allows us to treat fluids as continuous materials instead of discrete particles, making mathematical modeling viable.
Examples & Analogies
Consider a large crowd of people moving through a concert venue. Although each person is an individual (like particles), we often treat the crowd as a single entity for ease of understanding collective flow, akin to how we might treat a fluid as continuous.
Equilibrium of Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The equations reflect the equilibrium of forces acting on the fluid, including internal stresses, body forces, and momentum change within the control volume.
Detailed Explanation
This chunk explains how the Navier-Stokes equations are built on the principle of force balance within a fluid. It identifies the internal stresses (like friction within the fluid), body forces (like gravity), and momentum change as critical components in understanding fluid behavior.
Examples & Analogies
Think of a boat floating on water. The force of gravity acting downwards is balanced by the buoyant force from the water, while internal forces (like waves pushing against the hull) also affect how the boat moves through the water.
Structure of the Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The resulting equations show the relationship between different components such as density, velocity, pressure, and stress on fluid particles.
Detailed Explanation
This chunk highlights the comprehensive nature of the Navier-Stokes equations. They encapsulate the relationships between density, velocity, pressure, and stress, allowing us to model various fluid dynamics scenarios effectively.
Examples & Analogies
Imagine a symphony orchestra, where different instruments (representing density, velocity, pressure, and stress) must work together harmoniously to create a single performance. The Navier-Stokes equations are like the conductor, guiding these elements to ensure a seamless flow in fluid dynamics.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Continuum Hypothesis: A foundational assumption in fluid mechanics that fluids are continuous media.
-
Linear Momentum: A key quantity derived from the product of mass and velocity, essential for the Navier-Stokes equations.
-
Body Forces vs Surface Forces: Understanding the distinctions between forces acting throughout volume versus forces on surfaces.
-
Stress Tensors: Measurements of internal resistance in fluids, critical for understanding fluid interactions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The flow of water around obstacles like a bridge pier can be analyzed using the Navier-Stokes equations.
-
The calculation of airflow over an aircraft wing employs these equations to understand lift and resistance.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluid motion, stress we find, Cauchy leads, momentum aligned.
📖 Fascinating Stories
-
Imagine a flowing river encountering rocks. The water's motion is described by powerful equations, the Navier-Stokes, while the forces at work inside the water are told by Cauchy's equations.
🧠 Other Memory Gems
-
Remember 'B-S-S' for Forces - Body, Surface, Stress.
🎯 Super Acronyms
MVP - Momentum, Velocity, Pressure are the keys to flow equations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: NavierStokes Equations
Definition:
A set of nonlinear partial differential equations describing the motion of fluid substances.
-
Term: Cauchy Equations
Definition:
Equations that relate stress within a fluid to the rate of change of velocity.
-
Term: Stress Tensor
Definition:
A mathematical representation of the internal resistance forces within a fluid, described by components aligned with coordinate axes.
-
Term: Continuum Hypothesis
Definition:
An assumption that a fluid is continuous and properties like density are smooth functions of space and time.
-
Term: Body Force
Definition:
Forces acting throughout the volume of a fluid, such as weight or electromagnetic forces.
-
Term: Surface Force
Definition:
Forces acting on the surface of a fluid volume due to pressure or shear stress.