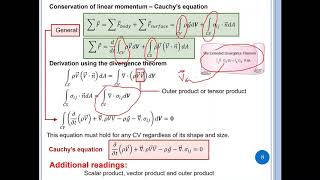
Cauchy's Equation
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Cauchy's Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning, everyone! Today we will begin our journey into fluid mechanics by discussing Cauchy's equation. Can anyone tell me why this equation is significant?

Is it because it helps us understand forces in fluid flow?

Exactly! Cauchy's equation helps us break down how stress within a fluid can be described mathematically. It serves as a base for our later exploration of the Navier-Stokes equations.

What kind of stresses are we looking at?

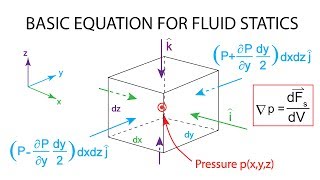
Great question! We particularly examine surface stresses, which affect fluid elements. Remember: Stress is the internal resistance per unit area.

Can you explain more about how stress relates to momentum?

Sure! The distribution of stress dictates how momentum is transferred through the flow—this relationship will be crucial as we derive further equations!

Let's summarize: Cauchy's equation illustrates the connection between stress, momentum, and fluid behavior. We'll explore stress tensors next.
Understanding Stress Tensors
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've introduced stress, let's talk about stress tensors. They help us understand the directional behavior of stress in fluids.

How do we visualize stress tensors?

Excellent question! Think of stress tensors as a 3x3 matrix representing how stress acts in three-dimensional fluid flow. For example, a tensor element might show stress acting in the x-direction on a yz-plane.

How do we calculate these stress components?

We rely on the continuum hypothesis, assuming that our fluid properties change smoothly across space. This allows us to use derivatives to evaluate stress states.

Can we connect this back to Cauchy's equation?

Absolutely! Stress tensors are crucial for deriving Cauchy’s equation and understanding how momentum and fluid flow interact. Let's summarize this: Stress tensors describe forces acting within fluids, enabling us to analyze motion more effectively.
From Stress to Momentum Flux
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's discuss momentum flux. Can someone explain how we determine changes in momentum in a control volume?

I think we look at the inflow and outflow of fluid across surfaces in that volume.

Exactly! By analyzing momentum flux across boundaries of the control volume, we can see how it changes with time.

Are these concepts applied in practical scenarios?

Yes! We apply these principles in computational fluid dynamics to solve complex flow problems. Understanding momentum changes leads us to form the differential equations that govern fluid flows.

To recap, understanding stress tensors helps us calculate momentum flux and the behavior of fluids in motion, which ultimately leads us toward deriving the fundamental equations of fluid mechanics.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section introduces Cauchy's Equation as a crucial stepping stone in deriving the Navier-Stokes equations. It outlines how Cauchy’s work underpins the understanding of fluid dynamics by conceptualizing stress tensors and their interrelations with momentum and body forces.
Detailed
Detailed Summary
Cauchy's Equation serves as a pivotal foundation in fluid mechanics, particularly in deriving the Navier-Stokes equations. The lecture emphasizes that while the mathematical representation may seem daunting, grasping the physical concepts can simplify understanding.
Key Takeaways:
- Differential Form of Momentum Equations: The section sets the stage for deriving linear momentum equations in differential forms through Cauchy's equations.
- Role in Computational Fluid Dynamics (CFD): It highlights the significance of understanding Cauchy’s Equation in mastering computational tools used for solving complex fluid flow problems.
- Continuum Hypothesis: The lecture elaborates on the continuum hypothesis that allows fluid flow characteristics to be modeled with smooth functions of space and time.
- Stress Tensors: A key focus is placed on stress tensors within fluids and the behavior of fluid particles under deformation.
- Mathematical and Physical Interpretations: Strategies for simplifying complex mathematical concepts are discussed to provide clarity on fluid dynamics phenomena.
Ultimately, this section prepares students to explore more advanced concepts in fluid mechanics by emphasizing the fundamental nature of Cauchy's equation.
Youtube Videos






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Cauchy's Equation
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Before deriving Navier-Stokes equations, we are going to derive Cauchy equations, which are very important equations for understanding the differential form of linear momentum equations.
Detailed Explanation
The Cauchy equations serve as a foundational element in fluid mechanics. They provide a mathematical framework to understand how momentum is conserved in a fluid flow. The importance lies in their application to computational fluid dynamics, which models complex fluid behaviors.
Examples & Analogies
Consider a river where water flows over a surface. Understanding how water moves and retains its momentum is crucial for designing bridges. Cauchy's equations help engineers predict how water will behave around the bridge supports.
Applications in Computational Fluid Dynamics
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Cauchy equations are the basic foundations of computational fluid dynamics. You can see what are the challenging problems we have been solving in this era of computational fluid dynamics.
Detailed Explanation
Computational fluid dynamics (CFD) utilizes mathematical equations, including Cauchy's equations, to simulate and analyze fluid flow problems. This makes it easier to visualize and predict the behavior of fluids in various scenarios, such as airflow over airplane wings or water flow in rivers.
Examples & Analogies
Imagine trying to predict how smoke disperses in a large area. By using CFD, engineers can simulate various conditions (like wind speed or obstacles) to understand how the smoke will spread, which can be vital in emergency scenarios.
Importance of Assumptions in Fluid Dynamics
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In deriving the momentum equations, we assume a continuum hypothesis, allowing us to consider fluid properties as continuous functions.
Detailed Explanation
The continuum hypothesis simplifies fluid mechanics by treating fluids as continuous materials, even though they are made up of discrete particles. This assumption enables us to apply calculus, using derivatives to understand how fluid properties change over space and time.
Examples & Analogies
Think of a jar filled with marbles. While the marbles have gaps between them, the fluid that fills those gaps can be thought of as a continuous layer. Analysing the flow of that fluid without considering the individual marbles makes calculations easier.
Role of Stress in Fluid Flow
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We will also talk about stress tensors in fluid flow, as in solid mechanics, focusing on how stress components interact within small control volumes.
Detailed Explanation
Stress in fluids is quite different from that in solids because it acts continuously throughout the fluid. Stress tensors express the internal forces per unit area acting within the fluid. These help in understanding how pressure and movement can affect the flow at any point.
Examples & Analogies
Consider stirring honey with a spoon. The stress created inside the honey allows it to flow smoothly. If you stir faster, the honey experiences greater stress and flows differently. Understanding this helps in designing better food processing equipment.
Momentum Flux and Control Volumes
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
To derive the equations, we consider these functions as parts of control volumes, looking at momentum flux and its variations.
Detailed Explanation
Control volumes are imaginary boundaries that help us analyze fluid flows. By observing the flow of mass and momentum across these boundaries, we can derive equations that describe how the fluid behaves over time and space. This observation is crucial for engineers to manage fluid systems effectively.
Examples & Analogies
Think of a water tank with multiple outlets. By analyzing how much water flows out through each outlet over time, we can ensure that our piping system is designed to avoid pressure buildup or leakage.
Deriving the Momentum Equations
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
By applying the Reynolds transport theorem, we derive equations that relate body forces and surface forces acting on the fluid within the control volumes.
Detailed Explanation
The Reynolds transport theorem links the rate of change of a quantity in a control volume to the flow of that quantity across the control surface. By analyzing surface forces (like friction) and body forces (like gravity), we can create momentum equations that apply to the fluid.
Examples & Analogies
Imagine a fire hose. The water pressure (body force) pushes the water out, while friction with the hose walls (surface force) affects how fast it comes out. Understanding these forces helps design hoses that deliver water efficiently.
Key Concepts
-
Cauchy's Equation: Fundamental for fluid dynamics and momentum analysis.
-
Stress Tensor: Represents forces acting within fluids in a matrix form.
-
Momentum Flux: Indicates how momentum moves through a control volume.
-
Continuum Hypothesis: Allows smooth analysis of fluid properties.
Examples & Applications
Visualizing stress tensors shows how internal resistance varies in fluid flow, acting as a matrix across multiple dimensions.
Momentum flux can be applied to predict changes in fluid behavior in real-life scenarios, such as water flowing through a pipe.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Cauchy, oh Cauchy, with flow so fine, stress moves like rivers, in fluid divine.
Stories
Once, a fluid named Cauchy traveled through pipes, encountering stress and momentum, building relationships across its path.
Memory Tools
Remember 'Slicing Cool Melons' for Cauchy’s: Stress, Continuum, Momentum.
Acronyms
CFS for Cauchy's Equation
Cauchy's stress formula.
Flash Cards
Glossary
- Cauchy's Equation
A fundamental equation in fluid mechanics that relates stress to fluid motion and momentum.
- Momentum Flux
The rate of transfer of momentum through a surface area, often related to the flow of fluid.
- Stress Tensor
A mathematical representation of internal forces within a fluid, described via a 3x3 matrix.
- Continuum Hypothesis
An assumption that fluid properties vary smoothly without abrupt changes, allowing for differential analysis.
Reference links
Supplementary resources to enhance your learning experience.
