Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Continuum Hypothesis
Unlock Audio Lesson
Good morning, everyone! Today we'll discuss the Continuum Hypothesis, which states that we can treat fluids as continuous matter rather than collections of individual molecules. This is essential for deriving equations in fluid mechanics.
Why do we need to assume fluid behavior is continuous?
Great question, Student_1! If we treat fluids as discrete particles, the equations governing their behavior would become extraordinarily complex. The continuum assumption allows us to simplify our calculations significantly.
So, we can still accurately describe fluid behavior by viewing it this way?
Exactly, Student_2! This simplification enables us to write differential equations that capture the essential dynamics of fluid flow.
In short, the continuum hypothesis is crucial because it allows us to apply calculus tools to fluids, leading us to equations like the Cauchy equations.
Deriving Cauchy's Equation
Unlock Audio Lesson
Now let’s derive Cauchy’s equations. Remember that Cauchy's equations are fundamental to understanding linear momentum in fluids.
What do these equations specifically represent?
Cauchy's equations describe how momentum changes in a fluid due to internal stresses. This is vital for later deriving the Navier-Stokes equations.
How do we link these equations to real-world applications?
Excellent inquiry, Student_4! These equations help model and predict fluid behavior in engineering, such as turbulent flows around structures.
In summary, understanding Cauchy’s equations and the continuum hypothesis is pivotal as we explore fluid dynamics further.
Importance of Stress Tensors
Unlock Audio Lesson
Let’s transition to the importance of stress tensors. These play a crucial role in assessing the internal resistance in fluid flow.
What do we mean by internal resistance?
Internal resistance refers to the forces within the fluid that oppose flow—represented mathematically as stress tensors. Understanding how these work helps us apply Newton's laws to fluids.
Can you provide an example of how this applies?
Certainly, Student_2! When fluid flows through a pipe, shear stress can lead to energy losses due to internal friction—a concept well-addressed by stress tensors.
In conclusion, stress tensors are fundamental in analyzing how the fluid’s internal mechanics affect overall flow behavior.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section provides a detailed exploration of the continuum hypothesis, key to understanding fluid dynamics. It sets the stage for deriving the Cauchy equations, which are crucial for establishing the Navier-Stokes equations, emphasizing the importance of stress tensors in fluid flow.
Detailed
Detailed Summary
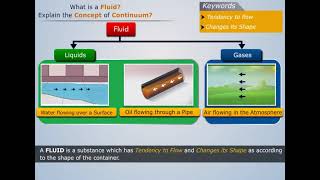
The Continuum Hypothesis in fluid mechanics posits that fluids can be treated as continuous mass rather than a collection of discrete particles. This concept is fundamental when deriving key equations governing fluid behavior, such as the Cauchy equations and the Navier-Stokes equations. The section emphasizes the significance of linear momentum equations in differential forms and how they underpin computational fluid dynamics (CFD). The instructor encourages students to relate theoretical concepts to practical applications in CFD, using software tools to visualize and solve fluid flow patterns.
The discussions involve complex fluid dynamics problems, such as analyzing velocity fields, pressure fields, and density variations, all influenced by the continuum hypothesis. Stress tensors, which characterize internal resistance (stress) within fluids, are also introduced as crucial elements in formulating the governing equations. The section pulls from classical fluid mechanics theories laid down since the 19th century, including references to the works of Cauchy and others who contributed to our understanding of fluid behaviors and interactions. The lecturer guides the learners toward understanding both theoretical and computational aspects, encouraging them to explore various educational resources.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Continuum Hypothesis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The continuum hypothesis states that fluid properties can be treated as continuous fields rather than discrete particles.
Detailed Explanation
The continuum hypothesis is a fundamental concept in fluid mechanics. It assumes that fluids are continuous materials, which means that instead of thinking of a fluid as being made up of individual particles, we treat it as having properties like velocity, pressure, and density that vary smoothly throughout space. This allows us to use mathematical equations, like the Navier-Stokes equations, to describe fluid motion. Without this assumption, analyzing fluid behavior would be incredibly complicated, as we would have to consider each particle's individual motion and interactions.
Examples & Analogies
Imagine a crowd of people at a concert. While you might originally think of each person as an individual with their own position and movement, to understand how the crowd is moving as a whole, it is easier to think of them as a fluid. Instead of tracking every single person's movement, you can consider the crowd's overall density and direction of motion, which represents the continuum hypothesis in action.
Implications of the Continuum Hypothesis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Using the continuum hypothesis allows for the use of mathematical tools to analyze fluid behavior efficiently.
Detailed Explanation
With the continuum hypothesis, fluid mechanics is able to utilize differential equations to model fluid behavior. The properties of velocity, pressure, and density in a fluid can be expressed as functions of space and time rather than needing to deal with individual molecules. This simplifies the analysis, allowing engineers and scientists to predict fluid flow behavior in various scenarios, such as airflow over an airplane wing or water flow in a pipe, using equations derived from the laws of physics.
Examples & Analogies
Think about how meteorologists predict the weather. They don’t look at each droplet of water in the atmosphere but instead analyze large areas of air as a continuous fluid. By applying the continuum hypothesis, they can use complex mathematical models to predict large-scale weather patterns instead of trying to track the behavior of each tiny water molecule.
Limitations of the Continuum Hypothesis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The continuum hypothesis may not hold at very small scales, such as in molecular dynamics or nanotechnology.
Detailed Explanation
While the continuum hypothesis is extremely useful, there are limitations. At extremely small scales, such as those involving gases at low densities or liquids at molecular levels, the assumption of continuity breaks down. In these cases, fluid properties must be addressed on a particle-by-particle basis. For example, in the study of gases at very high altitudes or nanofluids, where the movement of individual particles significantly affects the flow properties, the continuum model may not adequately describe the phenomena.
Examples & Analogies
Consider a grain of sand at the beach. If you look at the sand pile from a distance, it appears as a continuous mound. However, as you get closer and examine the individual grains, the continuous appearance breaks down, and you can see that it's made up of many separate particles. Similarly, on the microscopic level, fluids may behave more like ensembles of individual molecules rather than continuous materials.
Applications in Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The continuum hypothesis enables engineers to design systems that involve fluid flow, such as pipelines and airfoils.
Detailed Explanation
The applications of the continuum hypothesis are vast, particularly in engineering. It empowers the design and analysis of various systems that interact with fluids, including piping systems, hydraulic machinery, and aerodynamic surfaces. Engineers use the predictions made possible by the continuum assumption to optimize performance, increase efficiency, and prevent failures in these systems, ensuring they work as intended under various conditions.
Examples & Analogies
Think of how airplane wings are designed. Engineers use the continuum hypothesis to analyze airflow around wings to minimize drag and maximize lift. By applying mathematical models based on this hypothesis, they can predict how changes in wing shape will affect flight performance, allowing for safer and more fuel-efficient aircraft design.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Continuum Hypothesis: Treating fluids as continuous rather than discrete allows easier application of mathematical tools.
-
Cauchy Equations: Fundamental equations related to the motion of fluid elements in a continuum.
-
Stress Tensor: Represents internal forces within a fluid that oppose flow, crucial for analyzing fluid dynamics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a flowing river, the water can be treated as a continuum, allowing for calculations regarding velocity and pressure without needing to account for individual water molecules.
-
When analyzing the flow of air over an airplane wing, the continuum hypothesis simplifies the complex interactions between air molecules into manageable equations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the flow, we see no breaks, fluids merge, for math's sake!
📖 Fascinating Stories
-
Imagine a river flowing smoothly. Each drop flows seamlessly with its neighbors – this is how we treat fluids in physics – continuous and connected!
🧠 Other Memory Gems
-
Use 'C-C-S' to remember: C for Continuum, C for Cauchy, and S for Stress Tensor.
🎯 Super Acronyms
Remember 'FCS' for Fluid Continuity in Science!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Continuum Hypothesis
Definition:
The assumption that fluids are continuous masses rather than discrete particles, allowing for the use of calculus in fluid dynamics.
-
Term: Cauchy Equations
Definition:
Fundamental equations of motion for fluid mechanics that describe the momentum of fluid elements.
-
Term: Stress Tensor
Definition:
A mathematical representation of internal forces within a fluid that account for its resistance to deformation.
-
Term: NavierStokes Equations
Definition:
Equations that describe the motion of viscous fluid substances.
-
Term: Fluid Mechanics
Definition:
The study of fluids (liquids and gases) and the forces acting upon them.