Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Quasi Equations
Unlock Audio Lesson
Good morning everyone! Today, we will discuss quasi equations, which are crucial for understanding fluid mechanics. Can anyone tell me what they think quasi equations might involve?
Do they have something to do with the equations of motion in fluids?
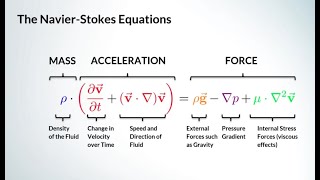
Exactly! Quasi equations lay the groundwork for the Navier-Stokes equations, which govern fluid motion. They help us analyze how fluids behave under different conditions.
Why are they considered 'quasi' equations?
Great question! The term 'quasi' indicates that these equations provide approximations to more complex dynamics. They simplify the modeling of fluid flows, allowing us to analyze complex scenarios effectively.
In essence, they connect fluid dynamics with our computational methods. Let's explore what these equations are by looking at Cauchy's equations next.
Cauchy’s Equation and Linear Momentum
Unlock Audio Lesson
Cauchy’s equations are a pivotal part of fluid mechanics. Can anyone summarize what this equation entails?
I think they describe how stress is distributed in a fluid?
Exactly! They relate the stress tensor to the rate of change of momentum in a fluid element. This is key for deriving the Navier-Stokes equations. What stresses do we typically consider in fluids?
We usually look at shear stress and normal stress.
Correct! Understanding both types of stress helps us analyze flow behavior. We will now look at how velocity fields are impacted by these stresses.
Momentum Flux and Control Volumes
Unlock Audio Lesson
Now, let’s discuss momentum flux within our defined control volumes. Can anyone explain what a control volume is?
Isn't it a specific region in which we analyze mass and momentum?
Exactly! We assess forces and flow within this volume. When we analyze momentum flux, what components do we need to consider?
We should account for both the incoming and outgoing momentum.
Exactly! The net change of momentum within that volume comes from what enters and leaves, represented mathematically during our derivation of the equations.
Application of Reynolds Transport Theorem
Unlock Audio Lesson
As we apply the Reynolds Transport Theorem to our discussions about momentum, how can we relate it to the surface and body forces?
We look at the gradients of momentum and how they change over time.
Right! Surface forces derived from stress tensors and body forces like gravity are both crucial in determining the overall force acting on our fluid systems.
So, does that mean we can combine those forces to derive the equations?
Exactly! Collectively, we can derive the equations that govern the fluid motion throughout our control volume, leading us towards our main goal of obtaining the Navier-Stokes equations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section delves into the derivation of quasi equations leading to the Navier-Stokes equations, emphasized as fundamental for computational fluid dynamics. The teacher aims to clarify complex mathematical concepts while discussing Cauchy's equations, momentum equations, stress tensors, and their applications in analyzing fluid flows.
Detailed
Quasi Equations
This section focuses on the derivation of quasi equations, which serve as crucial underpinnings for understanding fluid dynamics and leading towards the Navier-Stokes equations. The teacher aims to present mathematical intricacies in an accessible manner, emphasizing their significance in practical applications such as computational fluid dynamics (CFD).
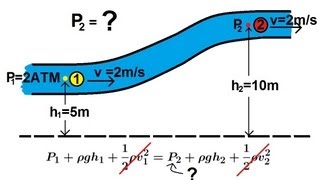
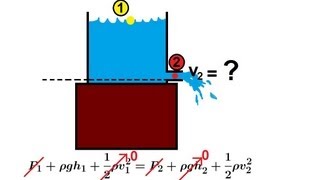
The discussion starts with Cauchy's equations, which form the foundation of linear momentum equations in their differential forms. The session highlights the importance of velocity fields, pressure, and density in the context of fluid dynamics, particularly when analyzing complex flows (like around bridge piers).
The derivation employs the continuum hypothesis and uses Taylor series expansions to simplistically approach infinitesimally small control volumes. The teacher introduces fundamental concepts like stress tensors, momentum equations, and the relationships among velocity, pressure, and density fields, reinforcing these concepts with visual sketches to illustrate flow behavior, distributions, and deformations.
By the end of the session, students will grasp the essential components of quasi equations, linking their understanding to real-world fluid mechanics problems, thereby setting the stage for their application in CFD challenges.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Quasi Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us go for today the derivations of Navier-Stokes equations. Before that quasi equations will derive it and which is a really important subject in the fluid mechanics to understand the computational fluid dynamics.
Detailed Explanation
In this part, the professor introduces the significance of quasi equations in the study of fluid mechanics. He mentions that these equations are foundational for understanding the Navier-Stokes equations, which describe how fluids move. Quasi equations are crucial for computational fluid dynamics (CFD), a field that applies numerical methods and algorithms to analyze fluid flows.
Examples & Analogies
Think of quasi equations like the basic rules of a game. Just as knowing the rules helps you play better, understanding these equations helps engineers predict and analyze the behavior of fluids in various contexts, such as designing bridges or airplanes.
Understanding Cauchy's Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Before deriving Navier-Stokes equations we are going to derive Cauchy equations which is very important equations when you go for differential form of linear momentum equations.
Detailed Explanation
The professor states that before tackling the Navier-Stokes equations, it's necessary to derive Cauchy's equations. These equations play a critical role in understanding the change in momentum of fluid particles. They form the foundation of the differential form of linear momentum equations, which is essential in fluid mechanics.
Examples & Analogies
Consider Cauchy's equations like the fundamental laws of motion that explain how an object moves under a force. Just as understanding these laws is essential for physics, Cauchy's equations are vital for understanding how fluids behave when forces are applied.
Significance of Computational Fluid Dynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Cauchy equations which is we will going to derive it which is the basic foundations of computational fluid dynamics.
Detailed Explanation
Here, the professor emphasizes that Cauchy's equations are foundational to computational fluid dynamics (CFD). CFD is used to simulate fluid behaviors in various applications, such as in engineering and environmental science. By understanding the principles behind these equations, students can grasp how they can be used to solve complex fluid flow problems.
Examples & Analogies
Imagine being able to simulate how water flows around a new bridge design before it’s built. CFD allows engineers to predict potential problems with fluid flow, helping to ensure that structures are safe and efficient.
Reference Materials
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, let us as I said it earlier that we follow the book of Sinzel Simbala book which is having a more interesting derivations as well as a series of illustrations which makes the problem which makes really the problems to understand the fluid mechanics problems.
Detailed Explanation
In this section, the professor recommends specific textbooks as resources for deeper understanding. He mentions 'Sinzel Simbala' as a key resource for its clear derivations and illustrations, which are important for visualizing fluid mechanics problems and concepts.
Examples & Analogies
Using a good textbook is like having a map when you’re in an unfamiliar place. It guides you through complex concepts and provides illustrations just as a map provides direction and landmarks.
Applications of CFD
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
we are solving the very basic things as I discussed in my first class is the velocity field, the pressure and the density. That is what we look at to solve velocity field, the pressure field and the density field.
Detailed Explanation
The professor explains that CFD helps in solving problems related to fundamental properties of fluid flow, such as velocity, pressure, and density. Understanding how these properties interact is essential for analyzing fluid behavior in various engineering applications.
Examples & Analogies
Think about how engineers need to know how fast water flows and how much pressure it has when designing a water treatment plant. CFD helps them visualize and calculate these factors before construction begins.
Deriving Navier-Stokes Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if I go for the next ones if you look it how do we get this computational fluid dimension solutions by solving these equations okay solving these equations which is known as very famous is Navier-Stokes equations.
Detailed Explanation
In this part, the professor transitions into discussing the derivation of the Navier-Stokes equations, which are fundamental to fluid mechanics. These equations govern the motion of viscous fluid substances. By understanding how quasi equations lead to these equations, students can appreciate the complex nature of fluid movement and the mathematical principles involved.
Examples & Analogies
Think of the Navier-Stokes equations as the ultimate recipe for predicting fluid behavior. Just like how a chef needs precise measurements to make a dish come out just right, engineers need accurate equations to predict how fluids will act in real life.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Quasi Equations: They serve as approximations to fluid dynamical equations, facilitating easier analysis.
-
Cauchy's Equations: Fundamental equations describing fluid stresses related to momentum changes.
-
Control Volume: A volume in which we analyze motion and forces of fluid flows.
-
Momentum Flux: Important measure of the momentum transfer rate, critical for fluid dynamics.
-
Reynolds Transport Theorem: A tool for linking quantities within a control volume to boundary flows.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The behavior of water flowing around a bridge pier can be analyzed using quasi equations to predict changes in velocity and pressure.
-
Cauchy's equations can be applied to determine stress distributions in a fluid contained within a pipeline.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To make fluid flow a breeze, quasi equations bring us ease!
📖 Fascinating Stories
-
Once upon a time, in a river flowing wide, Cauchy's equations revealed secrets hidden inside, showing how forces danced, and momentum thrived, turning complex fluid motion into knowledge derived.
🧠 Other Memory Gems
-
Remember C-R-M: Cauchy's equations, Reynolds Theorem, and Momentum flux - key elements of fluid flows!
🎯 Super Acronyms
FAME - Fluid Analysis Made Easier with quasi equations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Quasi Equations
Definition:
Equations that provide approximations to complex fluid dynamics, instrumental in deriving the Navier-Stokes equations.
-
Term: Cauchy's Equations
Definition:
A set of equations in fluid mechanics describing the stress distribution in fluid elements, critical for momentum dynamics.
-
Term: Momentum Flux
Definition:
The quantity of momentum per unit area flowing in and out of a control volume, crucial for analyzing forces in fluid dynamics.
-
Term: Control Volume
Definition:
A defined region in space used to analyze fluid flow and properties within its boundaries.
-
Term: Reynolds Transport Theorem
Definition:
A fundamental theorem used to relate the rate of change of a quantity within a control volume to its flux across the control surface.
-
Term: Stress Tensors
Definition:
Mathematical constructs that generalize the notion of stress to multi-dimensional spaces, representing internal forces within fluids.