Velocity and Pressure Fields
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Cauchy Equations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning class! Today, we’re going to dive into the Cauchy equations, crucial for understanding momentum in fluid mechanics. Can anyone tell me why these equations are important?

Are they important because they help us understand fluid motion?

Exactly! They help us describe how fluid velocity and pressure vary in space and time. Remember, Cauchy’s equations form the basis for the Navier-Stokes equations that we will cover later.

Isn’t the Navier-Stokes equations used in simulations?

Yes! It’s a cornerstone of computational fluid dynamics (CFD). Let’s keep this connection in mind as we explore further.

Can you give us an example of where Cauchy’s equations are used?

Absolutely! They are applied in weather prediction, aircraft design, and even in determining how fluids behave around structures.

Today’s takeaway: Cauchy's equation is fundamental for analyzing fluid dynamics and solving real-world flow problems. Keep this in mind!
Velocity and Pressure Fields
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s discuss how the velocity field varies with space and time. Why do we think these changes occur?

It could be due to changes in pressure or temperature.

Exactly! As pressure varies across different points in a fluid, so does velocity. This is modeled effectively using the Cauchy equations.

How do we visualize these changes?

Good question! We often use CFD to simulate these scenarios, allowing us to visualize fluid flow, pressure distribution, and density fields.

Are these simulations what engineers use to design bridges and buildings?

Yes, CFD allows engineers to calculate how structures will withstand fluid flow, which is critical for safety and effectiveness!

Key point: the relationship between the velocity field and pressure field is crucial for analyzing fluid dynamics.
Momentum Flux and Stress Tensor
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s move on to momentum flux. What do we understand about stress and its role in fluid?

Stress in fluids refers to internal resistive forces when they flow, right?

Exactly! The stress tensor defines these resistive forces per unit area, which are crucial for deriving the Cauchy equations.

Can you explain how we can use Taylor series here?

Sure! Taylor series help us approximate changes in stress and momentum over very small control volumes, allowing a better understanding of fluid dynamics.

How does this relate to the forces acting on the fluid particles?

Great inquiry! The accumulated forces within a control volume give rise to the momentum and contribute to the location's pressure and velocity fields, forming the Navier-Stokes equations eventually!

To summarize, understanding stress tensors and momentum flux is key to analyzing forces within fluid systems.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, the emphasis is on deriving the Cauchy equations, which play a crucial role in the differential form of momentum equations within fluid mechanics. The discussion extends to the exploration of velocity and pressure fields, utilizing computational fluid dynamics (CFD) as a tool to analyze flow characteristics.
Detailed
Velocity and Pressure Fields
This section delves into the derivation of the Cauchy equations, fundamental in understanding the differential forms of linear momentum equations in fluid mechanics. It highlights the necessity of these equations in computational fluid dynamics, a vital tool in solving complex fluid flow problems.
The discussion begins with an overview of linear momentum equations and their significance. The Cauchy equations provide a mathematical foundation for analyzing the velocity field, pressure field, and density fields, focusing on the relationship between these variables as functions of space and time.
By illustrating the changes in velocity fields around obstructions such as bridge piers using Cartesian coordinates, the complexities of fluid motion are simplified. The section emphasizes key assumptions like the continuum hypothesis and discusses the roles of stress tensors and the significance of applying Taylor series to derive necessary relationships.
Moreover, the section outlines various tensor equations that represent fluid stresses, facilitating deeper comprehension of the forces acting on fluid elements. Ultimately, this section encapsulates concepts crucial for mastering fluid dynamics and applies them to real-world scenarios through computational approaches.
Youtube Videos
![Introduction to Velocity Fields [Fluid Mechanics #1]](https://img.youtube.com/vi/CkNo5xGMZS4/mqdefault.jpg)








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Velocity and Pressure Fields
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
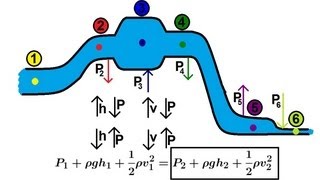
Let us before going to this, let I give a solution sheet, CFD problems, computational fluid dynamics problems where here we have used a CFD software is called flow 3Ds and we are solving the very basic things as I discussed in my first class is the velocity field, the pressure and the density. That is what we look at. That is what we look at to solve velocity field, the pressure field and the density field.
Detailed Explanation
In this section, we are discussing the core elements tackled using Computational Fluid Dynamics (CFD). It mentions the specific problems related to the velocity field, pressure field, and density field, which are fundamental to understanding fluid mechanics. By using CFD software like Flow 3Ds, we can model and analyze these fields to predict how fluids behave in different scenarios.
Examples & Analogies
Imagine a water slide. The flow of water down the slide represents the velocity field. The pressure at various points along the slide affects how fast and smoothly the water flows, similar to the pressure field in fluids. Just like observing how these factors affect the water slide’s performance, engineers use CFD to analyze real-world fluid scenarios.
Understanding Components of Velocity Field
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
When you have that problems, here we have considered a problems with a bridge pier. And here if you look at how the velocity field changes with the velocity field which has a component of scalar component and in three directions. Here I am looking just Cartesian coordinate systems. In that I have the uvw, so this is small v. the scalar component in x directions of velocity field which is a functions of space and the time.
Detailed Explanation
In this chunk, the focus shifts to analyzing the velocity field around a bridge pier, exemplifying how velocity varies in a fluid. The velocity field is described using components in a Cartesian coordinate system (x, y, z), employing variables u, v, and w to represent these components. It is emphasized that both space and time influence these scalar components, which is crucial in fluid dynamics.
Examples & Analogies
Think of a car driving on a highway where speed varies based on location (like the hill or valley of the road). In fluid dynamics, the velocity field acts similarly where different areas around an object, like a bridge pier, can have different flow speeds influenced by their position in space and time.
Pressure Field Characteristics
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
how do we get this computational fluid dimension solutions by solving these equations okay solving these equations which is known as very famous is Navier-Stokes equations. No doubt it has the limitations... these the velocity fields are changing it okay.
Detailed Explanation
This chunk outlines how the pressure field is analyzed through the Navier-Stokes equations in the context of CFD. These equations describe the motion of fluid substances and help in solving problems related to both velocity and pressure fields. Understanding these equations is essential as they depict the behavior of fluids under various forces, constraining our predictions within measurable limitations.
Examples & Analogies
Consider a balloon filled with air. The pressure inside the balloon is constantly changing based on how tightly the air molecules are packed and how they interact with each other—this reflects the essence of the Navier-Stokes equations in context, as they encapsulate changes in pressure as influenced by fluid motion.
The Role of Deformation in Fluid Flow
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
as you know it this is the particles are going it that is what will not be the same. Because there is a contraction there is a change of the velocity distributions it will the deformations here.
Detailed Explanation
The section focuses on the deformation of fluid particles as they move. Changes in velocity distributions lead to deformations within the fluid, which can be linear or shear types. Understanding deformation is critical in fluid dynamics, as it influences how fluid behaves and reacts under different conditions.
Examples & Analogies
Imagine kneading dough. As you apply pressure and move your hands through the dough, it stretches and changes shape. Similarly, when fluid particles move and interact, they undergo deformations which affect their flow characteristics.
Key Concepts
-
Cauchy Equations: Fundamental for fluid momentum analysis.
-
Velocity Field: Represents the velocity direction and magnitude at any point in the fluid.
-
Pressure Field: Represents how pressure varies in the fluid, affecting motion and behavior.
-
Continuum Hypothesis: Essential in treating fluids as continuous media for analysis.
-
Stress Tensor: Key in understanding internal forces acting in fluid elements.
Examples & Applications
Using CFD software to visualize fluid flow around structures like bridge piers.
Analyzing how changes in velocity and pressure affect fluid motion in real-world applications.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Cauchy’s equations pave the way, for momentum in fluid play.
Stories
Imagine a river flowing where pressure changes at bends causes the water to speed up or slow down. This is how velocity and pressure fields interact in nature.
Memory Tools
Remember C V P: Cauchy's, Velocity, Pressure - they all flow together.
Acronyms
VPC
Velocity-P pressure-Changes (reflects how pressure changes affect velocity).
Flash Cards
Glossary
- Cauchy Equations
Equations that describe the motion of fluid substances, foundational to the Navier-Stokes equations.
- Velocity Field
A vector field that represents the velocity of points in a fluid flow.
- Pressure Field
A scalar field representing the pressure at different points in a fluid.
- Continuum Hypothesis
An assumption that fluid properties can be defined at every point in space, treating the fluid as a continuous medium.
- Stress Tensor
A tensor that describes the internal resistive forces within a fluid per unit area.
Reference links
Supplementary resources to enhance your learning experience.
