Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Reynolds Transport Theorem
Unlock Audio Lesson
Good morning everyone! Today, we'll start by understanding the Reynolds Transport Theorem, commonly referred to as RTT. Who can tell me why understanding fluid flow through control volumes is important?
It's essential because it helps us analyze how fluids behave in different situations, like around objects.
Exactly! The RTT connects the rate of change of fluid properties inside a control volume to the flux across its surface. Who can explain 'flux'?
I think flux refers to how much of a property passes through a surface area per unit of time.
Right! It’s about how much is entering and leaving. This theorem allows us to derive equations like the Navier-Stokes. Can anyone tell me why those equations are significant in computational fluid dynamics?
They model the motion of fluid substances, which helps in predicting flow patterns.
Excellent! To recap, RTT provides a critical foundation for analyzing fluid dynamics. We'll explore its applications more deeply.
Momentum Flux and Body Forces
Unlock Audio Lesson
Let’s dive deeper into momentum flux. What is momentum flux, and how can we relate it to our understanding of fluid mechanics?
Momentum flux is the flow of momentum per unit area, right? It's calculated using the density and velocity of the fluid.
Exactly! We express momentum flux as ρu, where ρ is the density and u is the velocity. How does this relate to forces acting on a fluid?
I think it helps us understand how both body forces and surface forces are acting on fluids.
Well said! Body forces like gravity are critical, but so are surface forces related to stress tensors. These interrelate to give us the Net force which influences fluid behavior.
So, understanding these components helps us predict how fluids will behave when subjected to different forces?
Absolutely! For instance, it helps in CFD to model environmental factors. Perfect, let’s summarize these interactions!
Applications in Computational Fluid Dynamics
Unlock Audio Lesson
Now, let’s see how we can apply RTT principles in real-world scenarios, especially in CFD. Can someone share a scenario where these principles are crucial?
When designing bridges or dams, we need to analyze how water flows around them.
Exactly! Understanding how to model fluid dynamics around structures using RTT is crucial for safety and design efficiency. What challenges might engineers face while using these principles?
Different flow characteristics might complicate the predictions.
Yes! Flow turbulence and varying conditions can pose challenges. How does CFD help tackle these issues?
By simulating various scenarios, CFD can provide insights on optimizing design.
Well noted! In summary, RTT leads to better designs through simulations in engineering applications, making it an essential concept to grasp.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explores the Reynolds Transport Theorem, emphasizing its role in relating the integral forms of conservation laws to differential forms. It discusses the significance of momentum flux and body forces, illustrating how these concepts underpin the understanding of fluid dynamics and computational fluid dynamics.
Detailed
Reynolds Transport Theorem
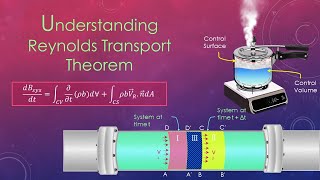
The Reynolds Transport Theorem (RTT) plays a crucial role in fluid mechanics, particularly in the analysis of fluid flows through control volumes. It provides a mathematical framework that links the rate of change of a physical quantity within a control volume to the flux of that quantity across the control surface.
Key Concepts Covered:
1. Fundamentals of RTT
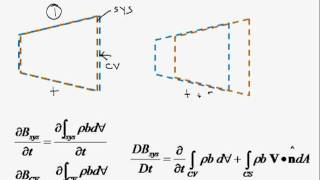
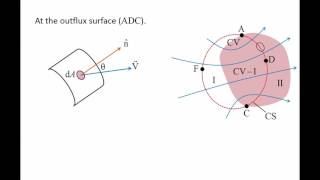
- The theorem states that the time rate of change of the property within a control volume can be expressed as the sum of the flux entering and leaving the control volume and the accumulation or depletion of that property within the volume itself.
2. Momentum Flux Components
- The theorem allows for the derivation of equations governing momentum, where the momentum flux is a fundamental concept. The momentum flux is defined as the product of mass flow rate and velocity, which also connects to stress tensors in the fluid.
3. Application to Fluid Dynamics
- By applying RTT, engineers derive the Navier-Stokes equations, which describe how the velocity field, pressure field, and density field interact over time. The RTT frames these interactions mathematically, aiding in the practical analysis of fluid flow problems, including real-world applications like those in computational fluid dynamics (CFD).
4. Practical Implications
- Understanding RTT is essential for analyzing complex fluid problems effectively, allowing predictions of how fluid behaves under various conditions, which is critical for engineering applications in civil engineering and environmental studies.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
What is the Reynolds Transport Theorem?
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Reynolds transport theorem involves applying the principles of conservation to a control volume, allowing for changes in mass, momentum, and energy within a fluid.
Detailed Explanation
The Reynolds Transport Theorem provides a framework to relate the changes in a quantity (like mass or momentum) in a fluid system to the effects of inflow and outflow across a control surface. It connects the changes inside the control volume to the net flow across its boundaries, making it essential in fluid dynamics for understanding how mass and momentum behave in fluid flows.
Examples & Analogies
Imagine a bathtub filling with water. The Reynolds Transport Theorem can help us understand how the water level is changing based on how fast water enters the tub and how fast it drains out when you pull the plug. Similarly, it helps in complex fluid flow scenarios where there are multiple inflows and outflows.
Components of Momentum as Described by the Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The theorem states that the rate of change of momentum in a control volume equals the net outflux of momentum across the control surface plus any forces acting on the system.
Detailed Explanation
The theorem quantitatively asserts that the change in momentum within a defined volume results from two main aspects: the momentum flowing out of the volume (net outflux) and the forces exerted on that volume (such as gravity). Thus, if we are monitoring how momentum is changing, we can establish equations that account for fluid entering and leaving the volume as well as any external forces acting on it.
Examples & Analogies
Think about a car accelerating on a road. Here, the engine generates force (acting on the car), propelling it forward and changing its momentum. Simultaneously, if another car merges onto the road, it contributes to the overall traffic flow—similar to how fluid enters and exits a control volume.
Surface Force vs Body Force Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In applying the Reynolds transport theorem, we differentiate between surface forces (due to stresses at the control surface) and body forces (due to gravity or other forces acting throughout the control volume).
Detailed Explanation
These two types of forces are crucial in determining the net forces acting on the fluid system. Surface forces result from stresses applied at the boundaries of the fluid volume, while body forces are distributed throughout the fluid, such as the force due to gravity. Understanding this distinction helps create accurate models of fluid behavior, as it allows us to account for all influences on the fluid's motion.
Examples & Analogies
Consider a balloon filled with air. The surface forces are the tension acting along the rubber of the balloon, while the body force is the weight of the air inside the balloon. When you let go of the balloon, the forces act together to change its overall momentum, demonstrating how both types of forces are integral to fluid dynamics.
Continuity and Continuum Hypothesis in Reynolds Transport Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The theorem assumes a continuum framework where variables such as density can vary continuously across the control volume, allowing for the usage of calculus to describe changes in motion and forces.
Detailed Explanation
This means that rather than treating fluids as composed of discrete particles, we assume a continuous mass distribution. This allows us to apply differential equations effectively and consider how properties like velocity and pressure change incrementally over space and time. The continuum hypothesis is vital for the derivations and solutions in fluid dynamics, making the mathematics manageable.
Examples & Analogies
Picture a crowded concert. Although there are many individual people, when observed at a distance, they can be treated as a continuous crowd. This analogy mirrors how fluids behave in small control volumes where the individual molecules blend into a smooth flowing continuum, making analysis possible using calculus.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
1. Fundamentals of RTT
-
The theorem states that the time rate of change of the property within a control volume can be expressed as the sum of the flux entering and leaving the control volume and the accumulation or depletion of that property within the volume itself.
-
2. Momentum Flux Components
-
The theorem allows for the derivation of equations governing momentum, where the momentum flux is a fundamental concept. The momentum flux is defined as the product of mass flow rate and velocity, which also connects to stress tensors in the fluid.
-
3. Application to Fluid Dynamics
-
By applying RTT, engineers derive the Navier-Stokes equations, which describe how the velocity field, pressure field, and density field interact over time. The RTT frames these interactions mathematically, aiding in the practical analysis of fluid flow problems, including real-world applications like those in computational fluid dynamics (CFD).
-
4. Practical Implications
-
Understanding RTT is essential for analyzing complex fluid problems effectively, allowing predictions of how fluid behaves under various conditions, which is critical for engineering applications in civil engineering and environmental studies.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When modeling water flow over a dam, engineers use RTT to calculate forces affecting the structure.
-
In wind tunnel testing, RTT helps analyze the airflow around a model to predict performance.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When the fluid flows, both fast and slow, RTT tells us where to go, to see its change and how it flows.
📖 Fascinating Stories
-
Imagine a river flowing through a dam. The RTT helps engineers decide how much water can be held upstream and how quickly it can flow down to keep the structure safe.
🧠 Other Memory Gems
-
Remember RTT: Rate of change, Through the surface, Transfer of flux.
🎯 Super Acronyms
RTT
- R: = Rate of change
- T: = Through
- T: = Transfer.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that relates the rate of change of a property in a control volume to the flow of that property across the control surface.
-
Term: Momentum Flux
Definition:
The product of mass flow rate and velocity, indicating the flow of momentum per unit area.
-
Term: Control Volume
Definition:
A defined volume in space through which fluid flows, often used to analyze fluid dynamics.
-
Term: Body Force
Definition:
Forces acting throughout the volume of a fluid (e.g., gravity).
-
Term: Surface Force
Definition:
Forces acting at the boundary of a control volume, usually calculated using stress tensors.