Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Cauchy's Equation
Unlock Audio Lesson
Good morning! Today, we will start with Cauchy's equation. Can anyone tell me what role this equation plays in fluid dynamics?
Is it related to the movement of fluid particles?
Exactly! Cauchy's equation describes how fluid elements move under various forces. It is fundamental for understanding fluid behavior. Remember: C for Cauchy, C for change. It's a great way to remember its significance!
How is it different from the Navier-Stokes equations?
Great question! While Cauchy's equation provides the groundwork, the Navier-Stokes equations offer detailed insights into fluid flow by incorporating viscosity and more complex forces.
I see. So, Cauchy's equation is a part of the bigger picture.
That's right! Just remember, it serves as a bridge to more complex equations in fluid dynamics.
Continuum Hypothesis
Unlock Audio Lesson
Now, let's shift to the continuum hypothesis. Who can explain what it means?
It's about treating fluids as continuous, right? Instead of discrete particles?
Exactly! By treating fluids as continuous, we can apply calculus to analyze their properties effectively, helping us develop differential equations like Cauchy's equation.
What does that imply for our calculations?
It means we can consider infinitesimally small control volumes, leading to more accurate models of fluid behavior. Think of it as ‘the smaller the better’ for precision!
Stress Tensors
Unlock Audio Lesson
Next, we’ll discuss stress tensors. What do you think tensors represent in fluid mechanics?
They probably describe how stress is distributed in the fluid?
Correct! Stress tensors quantify internal forces within the fluid. Each tensor component indicates how forces act on different planes. Remember, T for Tensor, T for Tension!
So, there are tensors for different directions?
Exactly! Tensors can have multiple components, and we use specific notation to distinguish their orientations!
Does that mean we should memorize the tensor notation?
Yes! Familiarize yourself with the notation; it will be essential as we delve deeper into equations and analyses.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
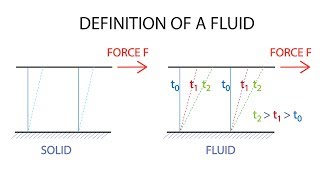
The section delves into essential definitions and notation relevant to fluid mechanics, with an emphasis on Cauchy's equations, which serve as the foundation for deriving the Navier-Stokes equations. It also discusses the continuum hypothesis, fundamental relationships between velocity, pressure, and density, and the importance of tensor notation.
Detailed
Definitions and Notation
Fluid mechanics relies heavily on a specific set of definitions and notations that are crucial for understanding and describing the behavior of fluid flows. In this section, we focus on Cauchy's equation, which lays the groundwork for deriving the Navier-Stokes equations critical for computational fluid dynamics (CFD).
Key Definitions and Notations
- Cauchy's Equation: Fundamental in fluid dynamics, it describes the motion of fluid elements under various forces.
- Continuum Hypothesis: Assumes that fluid properties can be averaged over infinitesimally small control volumes, allowing for differential calculus to apply effectively.
- Tensor Notation: Vital for describing stress states in fluids, tensors help represent the relationship between stress and strain rates in both solids and fluids.
Importance
Understanding these concepts is essential for advanced applications in CFD, as they enable the simplification of complex fluid behaviors into manageable mathematical equations. By grasping the notation and definitions, students will better comprehend the principles required for practical problem-solving in fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Stress in Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let me define it what are the trace. In case of let me look at this figure look at this figure same figures I am sketching again with components. Let I have component of X and I have a Y and I have a Z. This is the Cartesian coordinates and if I have a surface okay if I consider a surface which is a perpendicular to the X axis is a perpendicular to the X axis it is a parallel to the Y Z plane. is a parallel to the yz plane but is a perpendicular to the x directions. So when is that if I define the stress will be the sigma s the first subscripts indicates me it acting on a plane which is having a perpendicularity in the x direction.
Detailed Explanation
In fluid mechanics, the concept of stress is critical for understanding how forces affect fluid motion. Stress (C3) is defined as force per unit area and can be described in terms of its components. When we consider the Cartesian coordinates (X, Y, Z), we can describe how stress acts on different planes. For instance, if we have a surface that is perpendicular to the X-axis, the stress acting on it is labeled C3 (subscripted with X) to denote the direction. The subscripts indicate both the direction of the stress and the normal vector of the plane on which it acts, making it a tensor quantity, which is essential in the analysis of fluid motion.
Examples & Analogies
Think of stress in fluids like how water pressure acts against the walls of a swimming pool. The walls (the surface) experience pressure from the water in all directions. When the water is calm, the pressure is steady. If someone jumps in making waves, the stress (or pressure) changes on the walls momentarily, indicating how forces are transmitted through the fluid.
Understanding Stress Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The first subscript shows that on which plane it acts it if it makes a perpendicular that is which the directions. That is the perpendicular the plane where it is acting it and that perpendicular for or normal vectors follows the x directions that is the plane surface indicators are coming it. So if it is that I have a sigma xx that is what you can see that x is there I can write a sigma xx when I write same things in these directions it is acting on the same plane. So it will be sigma x and y as it is acting on the y directions.
Detailed Explanation
Understanding the notation of stress is vital for analyzing fluid mechanics. Stress components are expressed with specific subscripts indicating the orientation of the stresses. For example, C3xx indicates stress acting on a surface with a normal in the X direction. Similarly, C3xy would denote a shear stress acting on a surface with the normal in the Y direction while the force is applied in the X direction. This detailed notation helps engineers and scientists analyze forces acting on fluids and predict how they will behave under various conditions.
Examples & Analogies
Imagine you are pushing against a thick piece of glass: if you push straight on, that force creating stress is similar to C3xx, while if you push sideways against the glass, that would represent shear stress C3xy. Each stress tells you different things about how the glass will react to your push.
Trace Tensors in Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I take a surface the x y and that is what is please remember it in terms of subcrete notations that is what is this would not be can have a confusions here because what is a sigma xs what is a sigma xy what is sigma xz.
Detailed Explanation
Trace tensors are used in fluid mechanics to represent the state of stress at any point within a fluid. Each component of the stress tensor (e.g., C3xx, C3xy, C3xz) describes different types of stresses acting on fluid volumes. This tensorial approach allows us to summarize complex stress relationships into a manageable form that can be analytically studied, ultimately to derive fundamental equations that govern fluid flow.
Examples & Analogies
Visualize a spinning globe. Just like different areas (the poles vs. the equator) experience different stress levels from the globe's material strength, different points in a fluid flow can experience varying stress levels. The tensor notation captures that complexity, just like understanding the globe's dynamics requires looking at multiple points simultaneously.
Calculating Stress in Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In that I am defining the stress field. What do you mean by that? I am defining the internal resistance force what is happening it. per unit area because it is easy for me to derive it that is the reasons we talk about the trace.
Detailed Explanation
Calculating stress within a control volume involves looking at changes in forces acting on infinitesimally small elements of fluid. The internal resistance force per unit area, derived from stress components, helps in evaluating how the fluid reacts to external forces such as pressure or shear. The relationship between stress and internal forces is crucial when applying equations like the Navier-Stokes in fluid mechanics.
Examples & Analogies
Think of it as testing the surface of a sponge: if you push down on a sponge, you can measure the resistance based on how much you are pressing (force) over the surface area. In fluid mechanics, measuring internal stresses in small volumes helps predict how fluids will resist flow or change direction under pressure.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Cauchy's Equation: Fundamental equation in fluid dynamics which helps to understand fluid motion.
-
Continuum Hypothesis: Assumes fluids can be treated as continuous, allowing for calculus application.
-
Stress Tensor: Represents internal forces in fluid and is essential for analyzing stress distribution.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Cauchy's equation is used to describe the motion of water flowing through a pipe under pressure.
-
Example 2: Analyzing stress tensors helps to predict how fluids behave when subjected to external forces in different directions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Cauchy's equation in every flow, helps us see where the forces go.
📖 Fascinating Stories
-
Imagine a river as a continuous flow; it carries boats down below - that's why we use the continuum hypothesis.
🧠 Other Memory Gems
-
Use the acronym 'C-C-S' to remember: Cauchy's Equation, Continuum hypothesis, and Stress Tensor.
🎯 Super Acronyms
Remember 'CFS' - Cauchy, Fluid, Stress to recall the key concepts.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Cauchy's Equation
Definition:
A fundamental equation in fluid mechanics that describes the motion of fluid particles under various forces.
-
Term: Continuum Hypothesis
Definition:
An assumption in fluid mechanics that fluids can be considered continuous instead of discrete particles.
-
Term: Stress Tensor
Definition:
A mathematical representation of stress in a material, indicating how forces are distributed across different planes.