Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Drag Forces
Unlock Audio Lesson
Let's start by discussing drag. Who can tell me what drag force is?
Is it the force that slows you down when you're moving through air or water?
Exactly! The drag force is the resistance encountered by an object as it moves through a fluid. It's defined by the formula: FD = 0.5 * ρ * v² * Cd * A. Can anyone explain the variables in this formula?
ρ is the density of the fluid, v is the velocity of the object, Cd is the drag coefficient, and A is the frontal area!
Great job! Remember, minimizing drag is crucial for athletes because it allows them to maintain speed with less effort. What are some strategies athletes use to reduce drag?
Cyclists lean forward to create a smaller profile against the wind!
Perfect example. Leaning reduces the drag coefficient by decreasing the frontal area. Let's remember this with the acronym 'CD' for 'Cyclist Drag' reduction!
Exploring Lift Forces
Unlock Audio Lesson
Next, let’s talk about lift. Can someone explain what lift is in the context of sports?
Isn’t lift the force that helps objects rise or stay in the air?
You’re spot on! Lift acts perpendicular to the flow of air or water, and it's influenced by the shape of the object. We calculate it using: FL = CL * 0.5 * ρ * v² * A. What does CL represent?
It's the lift coefficient!
Exactly! Athletes like swimmers and gymnasts design their movements to maximize lift. How do you think a swimmer might adjust their technique for better lift?
They could streamline their body position to reduce resistance!
Good thought! It's similar to minimizing drag but focuses on maximizing upward forces. Remember, we're creating 'LIFTing' techniques!
Real-World Applications
Unlock Audio Lesson
Can anyone provide an example of how understanding drag and lift is crucial in a specific sport?
In cycling, aerodynamics can greatly impact speed!
Exactly! The design of bikes and the position of riders are engineered to minimize drag. What about with sports like tennis?
The spin on a tennis ball can create lift, affecting its trajectory.
Well done! The spin creates differences in air pressure, translating to lift. Let’s summarize: understanding these forces can lead to better performance in sports, from cycling to tennis!
Engineering and Design
Unlock Audio Lesson
Now, who can tell me how these principles apply beyond sports, in engineering?
It can help design wind turbines or cars to improve efficiency!
Correct! Engineers apply knowledge of drag and lift to optimize structures for performance. For instance, a wind turbine blade is designed to maximize lift for energy generation. In engineering, we often refer to this as creating a 'LIFTing Design'!
So this knowledge impacts not just athletes but also engineers!
Absolutely! This understanding connects fluid mechanics to real-world applications. Always keep in mind the interconnectivity of science and practical design!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concepts of drag and lift are explored through the lens of sports, illustrating how athletes and equipment are designed to optimize performance by reducing drag and enhancing lift. The mathematical relationships and practical implications are articulated through examples from cycling, swimming, and other sports.
Detailed
Detailed Summary
Aerodynamics is a critical component in sports, connecting fluid mechanics with athletic performance. This section elaborates on two primary forces, drag and lift, that athletes encounter and aim to optimize during sporting activities.
Key Points:
-
Drag Forces: Defined as the forces exerted by flowing fluid on bodies moving through it. An essential formula is introduced:
- Drag Force (FD) = 0.5 * ρ * v² * Cd * A, where:
- ρ = fluid density
- v = velocity of the object
- Cd = drag coefficient
- A = frontal area of the moving body
- Efficiency in Sport: Athletes, like cyclists, reduce their drag by optimizing body positions and gear. For instance, adjustments in posture can lead to significant reductions in drag coefficients.
- An example is given of a cyclist leaning forward, which can reduce their drag coefficient by approximately 20% compared to an upright position.
- Lift Forces: Lift is a force acting perpendicular to the flow direction and plays an essential role in the performance of athletes such as swimmers and gymnasts. The lift also adheres to a similar formula structure:
- Lift Force (FL) = CL * 0.5 * ρ * v² * A, where CL is the lift coefficient.
- Understanding the interplay between lift and drag allows athletes to optimize their movements and strategies.
- Practical Examples: The section cites examples in various sports, such as:
- Cyclists optimizing their aerodynamic profile
- Swimmers adjusting their body positions for better lift
- The dynamics of a spinning tennis ball, which can lead to rising or falling depending on the lift generated during its trajectory.
- Engineering Applications: The significance of these principles extends into engineering disciplines, influencing the design of wind turbines and automotive bodies to maximize efficiency and performance.
Overall, understanding the physics of drag and lift enhances athletes' performance and informs engineering practices in sports and transportation.
Youtube Videos
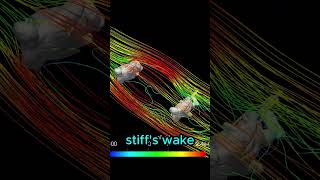
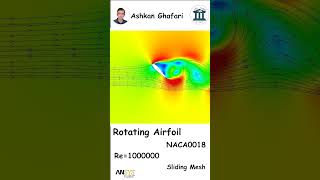
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Drag and Lift in Sports
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Good morning, let us have a today class on drag and lift which is the last class of this course okay. This is lecture number 36 and drag and lift. I think discussion of the drag and lift I started from the lecture number 2 where we illustrated how we can estimate it what will be the drag and lift forces of the towers. The And also we talk about this how the bars drag and lift forces in linear momentum equations.
Detailed Explanation
In this section, the instructor introduces the concept of drag and lift, relating it to the overall aerodynamics involved in sports. Drag and lift are aerodynamic forces that affect the performance of athletes using various sports equipment, such as bicycles or swimming gear. From previous lectures, the instructor has laid the groundwork on how to estimate these forces and their relevance to real-life scenarios in sports. Understanding drag and lift is crucial for optimizing performance, as these forces can significantly impact speeds and overall efficiency in competitive sports.
Examples & Analogies
Imagine a cyclist racing against others in the Olympics. Their position, clothing, and bicycle design all affect how air flows around them. By minimizing drag, they can go faster with the same amount of effort. This is akin to how a streamlined car is designed to reduce air resistance and improve fuel efficiency.
Minimizing Drag Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you look it that way I am not going more detail I again I am to encourage you just look it the very good illustrations are there and in the book of Sinzel-Cembala which gives you a lot of interest on the fluid mechanics if you look at the illustrations what is provided in Sinzel-Cembala book.
Detailed Explanation
The instructor emphasizes the importance of understanding drag and encourages students to explore visual resources, such as illustrations from the textbook by Sinzel-Cembala. These visuals can help clarify complex fluid mechanics principles more comprehensively. The foundational knowledge of drag characteristics is essential for athletes who want to optimize their performance by reducing the air resistance they encounter while competing.
Examples & Analogies
Think about how athletes like runners or swimmers wear tight-fitting clothing. This gear is designed to minimize drag from air or water, allowing them to move more swiftly and efficiently. Without such designs, they would struggle more against opposing forces while performing.
The Role of Cyclists in Reducing Drag
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When you have a cyclist driving a bicycles if you can look at recent Olympics and all if you see these persons lean seat okay as to reduce the drag forces it just leans it as going with so the basically minimizing the drag force so it leans up depending upon the speeds.
Detailed Explanation
Athletes, particularly cyclists, exploit their body position to decrease drag while racing. By leaning forward or adopting a streamlined posture, cyclists can reduce the frontal area exposed to wind, thus lowering the drag force significantly. The instructor notes that during competitions, even small adjustments in posture can have substantial impacts on performance due to the physics of drag and lift.
Examples & Analogies
Consider how a diver enters the water: they propel themselves downward, then tuck their body to minimize resistance when they hit the water. Similarly, cyclists adjust their bodies to cut through the air efficiently, showcasing a fundamental principle of aerodynamics at work.
Calculating Drag Force and Coefficients
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Most often we define the drag force is a functions of half rho v square multiplied with a Cd this is called coefficients of drag into A is the frontal area.
Detailed Explanation
The drag force can be mathematically represented by the equation F_d = (1/2) * ρ * v² * C_d * A. Here, ρ is the fluid density, v is the velocity of the object, C_d is the drag coefficient (a dimensionless value), and A is the frontal area of the object. This equation highlights how different factors contribute to the overall drag force, and understanding each component is crucial for athletes and engineers aiming to reduce drag in their designs and practices.
Examples & Analogies
Imagine you are trying to walk through water. If you wear a bulky wetsuit (larger frontal area), it feels much harder than if you wore a sleek swimsuit. Similarly, the drag coefficient changes based on the shape and smoothness of your body (or bicycle) interacting with the water (or air). Athletes meticulously design their gear to minimize A, C_d, and enhance performance.
Understanding Lift Force in Aerodynamics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you look at the drag okay which is a it is a very simple definitions as you can understand it that is a force flowing fluid exerted on a body in the flow direction is called the drag okay. Just normal to that components we can say that is that lift okay.
Detailed Explanation
The lift force is defined as the component of the aerodynamic force that acts perpendicular to the relative motion of the object through a fluid. While drag opposes the motion, lift helps to elevate or support the object against gravity, making it possible for aircraft, athletes, and even swimming strokes to perform optimally in their respective fields. The understanding of both drag and lift is crucial for a comprehensive view of fluid dynamics in sports.
Examples & Analogies
When an airplane takes off, its wings are designed to create lift. Similarly, when a swimmer uses the right stroke, they can create lift that helps them glide through water more effectively, much like how a bird takes flight by spreading its wings.
Practical Applications of Drag and Lift in Sports
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you look it for the circular case you have a frontal area d into L but in case of a rectangular case in the B so you know the frontal area you know this Cd value you know the design velocity you can always compute it what will be the drag force is very simple thing.
Detailed Explanation
Athletes and engineers can calculate expected drag and lift forces using parameters like frontal area and drag coefficient specific to their sport or equipment design. For circular and rectangular shapes, the calculation simplifies further since formulas relate directly to their dimensions and projective areas faced by the fluid. Utilizing these calculations allows for more efficient designs in sports equipment.
Examples & Analogies
Think of how car manufacturers design cars with different shapes to lower air resistance. In sports, similar strategies are employed—like the difference between a classic Sledge and a modern, streamlined bob sled. The latter is designed to minimize drag, allowing for faster runs and better control.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Drag: The force that opposes motion through a fluid.
-
Lift: The upward force acting perpendicularly to the fluid flow.
-
Drag Coefficient: A measure of the drag experienced relative to the fluid's density and velocity.
-
Lift Coefficient: A measure of the lift generated relative to the fluid's density and velocity.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A cyclist reduces drag by adopting a low aerodynamic position to increase speed during a race.
-
A swimmer streamlines their body position to achieve maximum lift and reduce drag through the water.
-
The spin on a tennis ball creates lift, affecting its path and allowing players to control its flight.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When in motion through the air, drag can really give you a scare!
📖 Fascinating Stories
-
Imagine a cyclist flying down a track, leaning forward to cut through the air, like a fish exploring the ocean depths, every curve controlled to minimize drag.
🎯 Super Acronyms
D-R-A-G
- Drag Resists All Going forward!
L-P-F for Lift, Pressure, and Frontal Area helps you recall lift's formula!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Drag Force
Definition:
The resistance experienced by an object in motion through a fluid.
-
Term: Lift Force
Definition:
The force acting perpendicular to the direction of motion in a fluid.
-
Term: Drag Coefficient (Cd)
Definition:
A dimensionless number that quantifies drag per unit area.
-
Term: Lift Coefficient (CL)
Definition:
A dimensionless number that quantifies lift per unit area.
-
Term: Frontal Area
Definition:
The cross-sectional area of an object facing the direction of motion.