Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Lift and Drag Forces
Unlock Audio Lesson
Good morning, everyone! Today, we are going to explore the concepts of lift and drag forces. Who can tell me what we mean by 'lift' in fluid mechanics?
Isn't lift the force that acts perpendicular to the flow direction?
Exactly! Lift acts vertically against the weight of the object. It is typically caused by pressure differences across the object’s surfaces. Now, what about drag? What is that?
Drag is the force acting parallel to the flow direction, opposing the motion of the object.
Correct again! So lift is what enables flight, while drag is what we try to minimize for efficiency. Remember: Lift is 'up,' and drag is 'back'—a good way to remember their directions!
Can the lift force be greater than the drag force?
Yes, in specific conditions, such as during a climb in an aircraft. It's essential for efficient flight. By the way, can anyone summarize how lift is generated?
Lift is generated by the difference in pressure on the upper and lower surfaces of the airfoil!
Perfect! Understanding these forces leads us to the coefficient of lift. Let's summarize this session: Lift acts upwards against weight, while drag opposes motion. Their relationship is crucial for flight dynamics.
Coefficient of Lift (CL)
Unlock Audio Lesson
Now that we understand the forces, let’s talk about the coefficient of lift, denoted as CL. What do you think CL measures?
It measures how much lift is produced relative to certain parameters, right?
Exactly! CL represents lift force as a function of dynamic pressure and the object's reference area. Remember this formula: CL = L / (0.5 * rho * v^2 * A). What does each component represent?
L is the lift force, rho is the fluid density, v is the flow velocity, and A is the reference area.
Spot on! Now, what factors can influence the value of CL?
The shape of the object, its angle of attack, and the flow conditions like Reynolds number.
Correct! Shape affects airflow, while Reynolds number tells us whether the flow is laminar or turbulent, impacting CL. To help remember, think of the acronym 'SARR'—Shape, Angle, Reynolds number, and reference area!
Can we measure CL experimentally?
Yes! We often use wind tunnels or CFD simulations to determine CL. Let’s summarize: CL measures lift relative to fluid dynamics, influenced by several factors, and is key in many engineering applications.
Practical Applications of CL
Unlock Audio Lesson
In our final session, let’s look at how CL applies in the real world. Who can give an example where CL is crucial?
In aircraft design! The wing shape greatly affects lift!
Exactly! Aircraft wings are designed to maximize lift while minimizing drag, especially during takeoff. Any other examples?
Cycling! Cyclists lean forward to reduce drag and increase speed.
Great point! Aerodynamics is incredibly important in sports. Cyclists aim for optimal positions to enhance lift and reduce drag. Can you connect this with lift forces?
Sure! Cyclists want to maintain lift while minimizing the drag that would slow them down.
Exactly again! Utilizing lift correctly can lead to better performance in various sports and engineering fields. Remember to always consider CL in design and performance. For our summary: CL connects theory and practice, influencing designs in aerospace, automotive, and sports.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The coefficient of lift (CL) is a crucial concept in fluid mechanics, particularly in aerodynamics, representing the lift force generated by an object in a fluid flow. This section explains how CL is affected by factors such as shape, size, flow velocity, and the Reynolds number, alongside its measurement through experimental and numerical methods.
Detailed
Coefficient of Lift (CL)
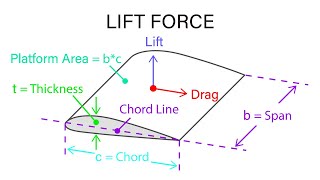
The coefficient of lift (CL) quantifies the lifting capabilities of a body in a fluid flowing around it. This concept is essential in fields like aerodynamics, marine engineering, and sports science. The lift force acts perpendicular to the flow direction, resulting from pressure differences and shear stresses acting on the body surface.
Significance of CL
- Design Applications: Knowing CL allows engineers and designers to develop efficient structures like aircraft wings, wind turbines, and high-rise buildings by optimizing their shapes for better lift performance.
- Measurement Techniques: CL can be measured experimentally through wind tunnel tests or computational fluid dynamic (CFD) simulations. Experimental determination provides empirical values, whereas numerical methods offer predictive capabilities.
Factors Influencing CL
- Body Shape: Different geometries yield different CL values due to changes in airflow patterns.
- Size: Larger bodies encounter more fluid, impacting the generated lift.
- Flow Velocity: Higher velocities increase dynamic pressure, resulting in higher lift values.
- Reynolds Number: This non-dimensional number characterizes flow regimes (laminar or turbulent) and affects CL.
Application Examples
- Cyclists: They adopt aerodynamic postures to reduce drag and enhance lift, which ultimately allows greater speed.
- Aircraft Wings: The design and angle of attack directly influence the CL, essential for takeoff and landing performance.
Understanding the coefficient of lift is vital for optimizing the design processes in various engineering applications, ensuring efficiency and performance.
Youtube Videos
![[Aero Fundamentals #5] Lift Coefficient Explained](https://img.youtube.com/vi/RlhQebKn9mk/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Lift and Drag Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The lift and drag forces are essential for understanding how objects move through fluid. Drag is the force exerted by flowing fluid in the direction of flow, while lift is the force that acts perpendicular to the flow direction.
Detailed Explanation
Lift and drag are two fundamental forces acting on a body in fluid flow. Drag is the resistance encountered by an object as it moves through a fluid, which acts in the same direction as the fluid flow. On the other hand, lift acts at a right angle to the flow direction and is primarily a result of pressure differences on the object's surface caused by the fluid's motion over it. Controlling both forces is crucial in designing efficient vehicles and structures.
Examples & Analogies
Imagine a car speeding down the highway. The air pushing against the front of the car creates drag, slowing it down. Now, think about an airplane wing; as air flows over and under the wing, it creates lift, helping the plane rise into the sky. This illustrates how lift can counteract gravitational forces.
Drag Coefficient (Cd) Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The drag coefficient (Cd) is defined as the drag force divided by the dynamic pressure and the frontal area. It is a crucial factor in determining how aerodynamic an object is.
Detailed Explanation
The drag coefficient is a dimensionless number that quantifies the drag or resistance of an object in a fluid environment. It encapsulates the effects of shape, size, and flow conditions. The formula to calculate it is: Cd = Fd / (0.5 * ρ * v² * A), where Fd is the drag force, ρ is the fluid density, v is the flow velocity, and A is the frontal area. A lower Cd value indicates a more aerodynamically efficient shape.
Examples & Analogies
Consider a soccer ball compared to a flat piece of paper. The soccer ball, being spherical, has a much lower Cd than the flat paper when thrown in the air, meaning it will face less drag and travel further and faster.
Coefficient of Lift (CL)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Similar to the drag coefficient, the coefficient of lift (CL) quantifies the lift force produced by an object in a fluid flow. It is calculated as the lift force divided by the dynamic pressure and the frontal area.
Detailed Explanation
The lift coefficient (CL) is a critical factor in aerodynamics, reflecting how much lift an object generates based on its shape, size, and the characteristics of the fluid flow. The formula is similar to that of the drag coefficient: CL = Fl / (0.5 * ρ * v² * A), where Fl is the lift force. A higher CL means that the object can generate more lift at a given speed and condition.
Examples & Analogies
When a plane takes off, its wings are designed to create a high CL by shaping the airfoil. As air moves faster over the wing's top surface compared to the bottom, it creates a lift force strong enough to elevate the aircraft into the sky.
Factors Influencing Cd and CL
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The coefficients of drag (Cd) and lift (CL) are influenced by several factors, including the shape and size of the object, fluid velocity, fluid density, Reynolds number, and surface roughness.
Detailed Explanation
Several factors affect Cd and CL values, such as the object's shape (streamlined vs. blunt), the fluid's properties (density and viscosity), and the flow conditions (laminar or turbulent). The Reynolds number, which characterizes the flow regime based on the object's size, speed, and fluid viscosity, plays a significant role. Additionally, a smoother surface can reduce drag, while a rougher surface might increase it due to higher turbulence.
Examples & Analogies
A good example would be comparing a sports car with a regular sedan. The sports car, designed with a sleek and smooth exterior, has a lower Cd, leading to better fuel efficiency at high speeds compared to the sedan, which has a bulkier design.
Applications of CL and Cd in Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In engineering, understanding and applying the concepts of CL and Cd is crucial for designing efficient vehicles, buildings, and other structures subjected to fluid flow.
Detailed Explanation
Engineers use the principles of lift and drag coefficients to design vehicles that can minimize resistance and maximize performance. For example, in designing aircraft, engineers analyze wing shapes to optimize lift for takeoff and maneuverability while minimizing drag for fuel efficiency. Similarly, in civil engineering, the drag coefficient plays a vital role in designing tall buildings and structures to withstand wind forces.
Examples & Analogies
Think of how race cars are designed with special shapes and features like spoilers, which enhance their aerodynamics. These design choices focus on lowering drag and maximizing lift to improve speed and stability on the racetrack.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Lift Force: The force acting perpendicular to the flow direction, generated by pressure differences.
-
Drag Force: The force acting in opposition to motion, parallel to the flow direction.
-
Coefficient of Lift (CL): A measure of lift generation relative to dynamic conditions.
-
Reynolds Number: A parameter that characterizes flow types and influences CL.
-
Angle of Attack: The angle affecting lift generation and drag.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An aircraft wing designed to optimize lift by varying its angle of attack.
-
A cyclist adopting a low-profile position to reduce drag and improve speed.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Lift goes up to let you fly, while drag will try to pull you by.
📖 Fascinating Stories
-
Imagine an airplane preparing for takeoff; it angles its wings to create lift while battling drag, much like a dancer balanced delicately on the edge.
🧠 Other Memory Gems
-
Remember CL: Create Lift by looking at dynamic conditions—Shape, Angle, Reynolds number.
🎯 Super Acronyms
LARD
- Lift
- Angle of attack
- Reynolds number
- Drag - key factors affecting lift force.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Coefficient of Lift (CL)
Definition:
A dimensionless number that relates the lift force to the product of dynamic pressure and reference area.
-
Term: Dynamic Pressure
Definition:
The pressure exerted by a fluid in motion, calculated as 0.5 * rho * v^2.
-
Term: Reynolds Number
Definition:
A dimensionless number that indicates the type of flow (laminar or turbulent) based on the fluid's velocity, density, and viscosity.
-
Term: Angle of Attack
Definition:
The angle between the oncoming airflow and the chord line of an airfoil.
-
Term: Aerofoil
Definition:
A shape designed to generate lift when air flows over it.