Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Drag and Lift Forces
Unlock Audio Lesson
Good morning, class! Today we will discuss drag and lift forces. Can anyone tell me what drag force is?
Isn't drag the force that opposes an object in motion through a fluid?
Exactly! Drag is the resistance force exerted by fluid flow on an object, and it's essential in designs like cars and airplanes. Now, what about lift?
Lift is the upward force that helps an object, like an airplane wing, rise against gravity?
Correct! Lift is generated when there’s a pressure difference across the surfaces of the wings or other objects. Let's remember - Drag and lift are crucial in both engineering designs and sports.
Can we use a mnemonic to remember these concepts?
Sure! You could use 'LIFT' for 'Lift In Fluid is Thrust' and 'DRAG' for 'Diminishing Resistance Against Gravity.'
Understanding Drag Coefficients
Unlock Audio Lesson
Now, let’s talk about drag coefficients. Why do you think they are important in engineering?
They help us understand how much force we need to overcome drag.
Precisely! The drag coefficient (Cd) is a function of the shape, size, and orientation of the object. What did we find can reduce Cd?
Adjusting the shape and position can lower Cd.
Right! Factors like the body’s orientation, as seen with cyclists leaning forward, can significantly impact drag forces. Let's take a moment to remember: 'Less is More' in terms of surface area and shape!
Practical Applications of Wind Tunnel Testing
Unlock Audio Lesson
In today's world, where are drag and lift applied outside of cars and planes?
What about in sports, like cycling or swimming?
Exactly! Athletes use techniques to minimize drag, just like in engineering designs. For instance, swimmers streamline their bodies to enhance lift and reduce drag.
So, wind tunnel testing is crucial for both engineering and athletic performance?
Yes! Wind tunnels allow us to visualize and measure the effects of air flowing over objects, facilitating optimal designs. Always think: 'Test, Measure, Improve!'
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the focus is on the importance of understanding drag and lift forces, particularly in the context of wind tunnel testing. It provides insights on how these forces impact the design of vehicles, wind turbines, and even athletes in competitive sports, highlighting the key parameters influencing drag coefficients.
Detailed
Detailed Summary of Wind Tunnel Testing
Wind tunnel testing plays a crucial role in understanding drag and lift forces in fluid mechanics. These forces significantly affect the design and efficiency of various structures and vehicles, including cars, wind turbines, bicycles, and airplanes. In designing fuel-efficient cars and effective wind turbines, engineers rely heavily on data obtained from both experimental tests and computational fluid dynamics (CFD).
The drag force is defined as the force exerted by a fluid flowing against a body, proportional to the square of the flow velocity, the fluid density, and the frontal area presented by the body. The drag coefficient (Cd) is a dimensionless number that quantifies the drag or resistance of an object in a fluid environment. Understanding the factors influencing Cd, including the shape and orientation of the body, is vital for minimizing drag during design phases.
Practical examples, such as athletes adjusting their body positions to reduce drag in sports events, demonstrate the real-world implications of these concepts. Furthermore, fundamental principles like boundary layer theory, pressure difference, and turbulent flow all intertwine with drag and lift considerations, influencing aerodynamic designs.
The section emphasizes the necessity of precise measurements of drag and lift forces through wind tunnel tests to achieve better design outcomes and energy efficiency.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Drag Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The drag force is defined as a function of half the fluid density (ρ), the square of the velocity (v²), and the drag coefficient (Cd) multiplied by the frontal area (A). Therefore, the relation can be summarized as:
\[ F_d = \frac{1}{2} \rho v^2 C_d A \]
The drag coefficient (Cd) can be estimated through experiments conducted in wind tunnels or through numerical simulations.
Detailed Explanation
Drag force is the resistance experienced by an object moving through a fluid (like air or water). It depends on the characteristics of the fluid and the object’s shape, size, and orientation. The relationship involves fluid density, velocity, drag coefficient, and the object’s frontal area. For instance, a cyclist leans forward to reduce their frontal area against the oncoming air, thus lowering the overall drag force they experience.
Examples & Analogies
Imagine riding a bicycle on a windy day. If you sit upright, more air hits your body, and you experience greater drag. However, if you lean forward, you present a smaller surface area to the wind, reducing drag and allowing you to go faster with less effort. This is similar to how race cars are designed to be low and streamlined.
Effects of Shape and Orientation on Drag
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The drag coefficient (Cd) changes with the shape and orientation of the object. For example, if a cyclist bends forward, their Cd value can decrease by 20%, drastically reducing drag. Similarly, the orientation of objects like umbrellas has a significant impact on the drag force experienced.
Detailed Explanation
The shape and orientation of an object greatly influence how air flows around it, thereby affecting the drag force. Objects with more streamlined shapes experience less drag than flat surfaces, as they allow air to flow more smoothly over them. For example, an umbrella held upright experiences more drag than when it is tilted with the wind. Understanding these principles helps in designing vehicles and aerodynamics for sports.
Examples & Analogies
Consider a car windshield: a sloped windshield allows air to flow over it smoothly, while a vertical flat windshield creates a larger area for air to push against, increasing drag. This is why many sports cars have sleek designs that minimize drag and improve speed.
Wind Tunnel Testing in Practice
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
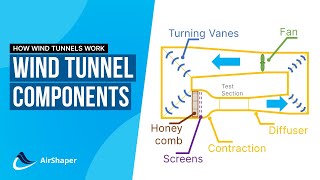
Wind tunnel tests are vital for measuring the drag coefficient (Cd) of various shapes. By conducting these tests, engineers can gather data on how different designs perform under specific conditions, allowing them to adjust designs to minimize drag.
Detailed Explanation
Wind tunnels simulate the conditions an object would face when moving through air. Engineers place a model of the object in the tunnel and measure the forces acting on it to determine its drag coefficient. This testing is crucial for industries like automotive and aerospace, where reduced drag leads to improved fuel efficiency and performance.
Examples & Analogies
Think about how race car teams use wind tunnels to test their car designs. They create scale models of the cars and place them in the wind tunnel to see how well they cut through the air. By adjusting features like spoilers and body shape based on the results, they optimize the car for speed and fuel efficiency, much like how athletes refine their techniques for better performance.
Role of Reynolds Number in Drag Coefficients
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The drag coefficient (Cd) varies depending on the Reynolds number, which characterizes the flow of fluid around the object. At low Reynolds numbers, drag is primarily due to viscous effects, while at high Reynolds numbers, inertial effects take precedence.
Detailed Explanation
Reynolds number is a dimensionless quantity that helps predict flow patterns in different fluid flow situations. Low Reynolds numbers indicate laminar flow, where fluid moves in parallel layers, leading to higher drag coefficients. Conversely, high Reynolds numbers indicate turbulent flow, which can reduce the drag coefficient. This relationship is key for understanding how objects perform at different speeds.
Examples & Analogies
You can relate the Reynolds number to the difference between stirring thin soup and thick syrup. In the soup (low viscosity), the flow is smooth and layers slide easily, but in the syrup (high viscosity), the drag is higher, making it harder to stir. This illustrates how viscosity affects fluid behavior around objects.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Drag Force: The resistance experienced by an object moving through a fluid.
-
Lift Force: The upward force on an object due to pressure differences.
-
Drag Coefficient (Cd): Critical for understanding and reducing drag in designs.
-
Wind Tunnel Testing: An essential method in aerodynamics to assess performance.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A cyclist leaning forward reduces air resistance, minimizing drag.
-
Athletes optimizing body shape in sports like swimming to enhance lift.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When rocks roll fast but the wind blows slow, drag helps us know where the flow will go.
📖 Fascinating Stories
-
Once there was a cyclist named Leo, who wanted to win a race. He learned about lifting his body to dance with the wind, reducing drag, and flying smoothly past all his friends.
🧠 Other Memory Gems
-
'LIFT' for 'Lift In Fluid is Thrust' helps us remember how lift is produced.
🎯 Super Acronyms
'DRAG' stands for 'Diminishing Resistance Against Gravity'; it symbolizes the force trying to slow us down.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Drag Force
Definition:
The force exerted by a fluid flowing against a body in the direction of the flow.
-
Term: Lift Force
Definition:
The upward force generated by pressure differences on an object, typically perpendicular to the flow direction.
-
Term: Drag Coefficient (Cd)
Definition:
A dimensionless number that quantifies the drag or resistance of an object in a fluid environment.
-
Term: Wind Tunnel Testing
Definition:
An experimental method used to measure aerodynamic properties of objects by simulating airflow around them.
-
Term: Boundary Layer
Definition:
The thin layer of fluid near a surface where effects of viscosity are significant, resulting in velocity gradients.