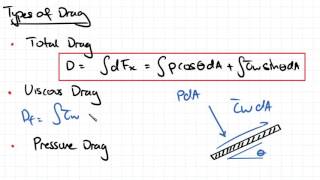
Total Drag Components
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Drag Components
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning, class! Today, we're diving into the concept of drag. Can anyone tell me what drag is and why it matters in fluid mechanics?

Drag is a force opposing the motion of an object moving through a fluid, right?

Exactly! Drag acts in the opposite direction to motion and is influenced by factors such as the object's shape, size, and surface texture. Do you remember the two main components of drag?

Isn't it frictional drag and pressure drag?

That's right! Let’s break those down: frictional drag is due to the fluid's viscosity and the object's surface, while pressure drag results from pressure differences around the object. Remember, 'Frictional is from touch; Pressure is due to flow!'

Got it! So, how do these different types of drag affect performance in racing bikes?

Great question! Racers lean forward to minimize their frontal area, reducing both types of drag. Remember: lower drag equals higher speed!

So in summary, drag is a significant force opposing motion in fluids. It's essential to design streamlined shapes to minimize it. Let's move on to how we can quantify these impacts with drag coefficients.
Understanding Drag Coefficients
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, does anyone know what a drag coefficient (Cd) is?

Is it a number that helps quantify how much drag an object experiences?

Exactly! The drag coefficient depends on the shape, surface roughness, and flow conditions. It's calculated using the formula: Drag Force equals 1/2 * Cd * ρ * V² * A. Can you identify all the components in this formula?

Cd is the drag coefficient, ρ is the fluid density, V is the velocity, and A is the frontal area!

Correct! It's important to understand how adjusting each factor can affect the drag force. Who can give me an example of how this might apply to, say, a cyclist?

If a cyclist wears tight-fitting clothing, wouldn't that reduce the frontal area and lower Cd?

Absolutely! This shows how practical and necessary it is to optimize shape and area for better performance.

In summary, drag coefficients are essential tools to understand and calculate the effects of drag on various objects. Let's now explore more examples of drag in different shapes.
Real-Life Applications of Drag Concepts
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s focus on how drag plays a role in everyday situations. Who can think of a practical example?

In swimming! Swimmers try to reduce drag by positioning themselves correctly in the water.

Great example! Their body position and clothing can greatly affect their drag and, ultimately, their speed. Can anyone think of another example?

What about cars? They’re designed with streamlined shapes to minimize drag.

Exactly! Lower drag can lead to higher fuel efficiency. Remember the concept: 'Streamlined shapes mean speed and efficiency!'

I see how much engineering goes into design to reduce drag.

Yes, and understanding drag components helps engineers make informed decisions. Just think of this: Whether it's cars, athletes, or even buildings in wind, drag matters!

To sum up, drag affects efficiency and performance across many activities. Keep these examples in mind as we wrap up.
Final Thoughts and Interconnections
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

As we wrap up these discussions, let’s reflect on how everything is interconnected. Why is understanding the components of drag important?

It helps in optimizing the performance of various objects!

Correct! Whether it's for athletic training, vehicle design, or even architecture, drag plays a vital role. Can you give a summary of the two main types of drag we discussed?

Frictional drag depends on the object's surface and its interaction with the fluid, while pressure drag is due to pressure differences.

Well done! Lastly, remember the equation with Cd as a critical element in calculating drag forces. It measures efficiency and shapes performance.

In conclusion, understanding drag components is essential in various fields. Thank you all for your participation!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore the essential components of drag, including frictional drag and pressure drag, and their relationships with the shapes and orientations of objects. The discussion includes practical examples, the importance of drag coefficients in engineering applications, and how these principles can be observed in everyday scenarios involving cyclists, athletes, and vehicles.
Detailed
In fluid mechanics, drag is defined as the force exerted by a fluid on a body moving through it, and it has critical implications in design and performance across various applications such as aerospace and automobile industries. This section elaborates on the various components of drag, primarily dividing them into frictional drag, which arises from the contact of the fluid with the surface of an object, and pressure drag, which results from the difference in pressure acting on different sides of the object due to fluid flow. The drag coefficient (Cd) serves as a crucial factor, demonstrating how drag force varies with object shape, orientation, and flow characteristics. Practical examples such as the design of racing bicycles and the behavior of different objects like umbrellas and aerodynamic shapes illustrate the real-world significance of understanding drag components.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Drag and Lift
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Drag is defined as the force exerted by the flowing fluid on a body in the direction of flow. In contrast, lift is perpendicular to the flow direction. They are both crucial in designs like fuel-efficient cars and wind turbines.
Detailed Explanation
In fluid mechanics, drag and lift are two fundamental forces that act on objects moving through a fluid (like air or water). Drag is the resistance that a body faces when it moves through a fluid. It acts in the same direction as the fluid flow. Lift, on the other hand, is the force that acts perpendicular to the direction of fluid flow. The understanding of these forces is essential for designing vehicles, structures, and various engineering applications because they dictate how efficiently an object can move through a fluid.
Examples & Analogies
Consider a cyclist riding on a flat road. The air flow creates drag, which slows down the cyclist. To reduce this drag, cyclists often lean forward, which decreases their frontal area exposed to the wind. In contrast, if we think about an airplane wing, as air flows over it, it creates lift, allowing the airplane to rise into the sky.
Factors Influencing Drag Force
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The drag force can be expressed as FD = 0.5 * rho * v² * Cd * A, where rho is the fluid density, v is the velocity, Cd is the drag coefficient, and A is the frontal area.
Detailed Explanation
The drag force (FD) acting on an object moving through a fluid can be calculated using the formula: FD = 0.5 * rho * v² * Cd * A. In this formula, 'rho' represents the density of the fluid, 'v' is the velocity of the object relative to the fluid, 'Cd' is the drag coefficient which depends on the shape and surface characteristics of the object, and 'A' is the frontal area of the object facing the flow. Understanding this equation helps in predicting and minimizing drag force in designs, leading to improved performance.
Examples & Analogies
Think about a car designed for racing. Engineers use wind tunnel tests to determine its Cd and optimize its shape to minimize drag. A streamlined shape, like a teardrop, has a lower drag coefficient compared to a boxy shape, helping the car go faster while using less fuel.
Effect of Drag Coefficient on Performance
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The coefficient of drag (Cd) varies with shape, size, and orientation of the object. Reducing Cd is critical for competitive athletes like cyclists, who aim to minimize drag to enhance performance.
Detailed Explanation
The drag coefficient (Cd) is a dimensionless number that represents how aerodynamic or hydrodynamic a particular shape is. Cyclists and racing drivers strive to reduce their Cd because even a small decrease can lead to significant performance improvements. For example, a slight change in body position can lower the Cd, reducing drag and allowing athletes to travel faster.
Examples & Analogies
Imagine a swimmer in a pool. If they keep their arms and legs close to their body (a more streamlined position), they encounter less water resistance (drag) than if they flail their limbs. This principle also applies to cyclists bending forward to reduce drag when racing, which can significantly improve their speed over a long distance.
Calculating Drag Force in Real-Life Scenarios
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Experiments can estimate drag force using wind tunnels or computational fluid dynamics (CFD). For example, changing the orientation of an umbrella in the wind can significantly affect drag due to changes in Cd.
Detailed Explanation
Drag force can be experimentally determined in a controlled environment using wind tunnels or CFD simulations. By changing the shape or orientation of an object in these tests, engineers can measure how drag changes, as demonstrated by adjusting the orientation of an umbrella against the wind, which can triple the drag due to a change in Cd.
Examples & Analogies
Consider riding a bike with an umbrella held straight against the wind versus tilted at an angle. When straight, the umbrella catches more wind, producing a high drag force. When tilted, it faces less wind resistance, demonstrating how orientation affects drag.
Key Concepts
-
Drag Force: Opposes the motion of an object in a fluid.
-
Frictional Drag: Caused by the fluid's interaction with the object's surface.
-
Pressure Drag: Results from pressure differences as fluid flows around an object.
-
Drag Coefficient (Cd): A measure of an object's drag characteristics.
-
Frontal Area: The projected area of an object in the direction of fluid flow.
Examples & Applications
A cyclist leans forward to reduce their frontal area and minimize drag.
An umbrella positioned against the wind experiences higher drag compared to when tilted.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In cars and planes they take the lead, drag is a force you don’t need.
Stories
A cyclist, aware of the wind's push, leans forward like a fish in a rush, to cut through the air with better speed, minimizing drag, that's the athlete's creed.
Memory Tools
Remember: 'Friction cancels flow, Pressure makes it slow!' to distinguish between drag types.
Acronyms
Remember 'D-FP' for Drag - Friction and Pressure to quickly recall drag components.
Flash Cards
Glossary
- Drag Force
The force exerted by fluid on a body opposite to the direction of movement.
- Frictional Drag
The component of drag due to the viscosity of the fluid and the surface of the object.
- Pressure Drag
The component of drag that results from pressure differences acting on the surface of an object in a fluid.
- Drag Coefficient (Cd)
A dimensionless number that describes an object's drag characteristics in a fluid.
- Frontal Area
The area of the object projected in the direction of flow.
Reference links
Supplementary resources to enhance your learning experience.
