Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Friction Drag
Unlock Audio Lesson
Let's start with friction drag. It's the force that opposes the motion of an object through a fluid due to viscosity. Can anyone tell me what factors influence this drag?
I think it has to do with the surface roughness of the object.
Exactly! Surface roughness and the fluid's dynamic viscosity play significant roles in determining friction drag. Remember, smoother surfaces tend to have lower friction drag. Can you think of examples of objects that would experience this?
Like a fish moving through water — it has a smooth body to reduce drag.
Great example! So friction drag is crucial for animals and objects moving through fluids. Let's summarize: friction drag depends on viscosity and surface characteristics.
Drag Coefficients
Unlock Audio Lesson
Now, let's examine the drag coefficient formula. Who can tell me what this formula is?
It’s $ F_d = rac{1}{2} C_d \cdot \rho \cdot v^2 \cdot A $.
Correct! The drag coefficient $C_d$ is affected by factors like the object's shape and the Reynolds number of the flow. Does anyone know what a Reynolds number signifies?
It's a measure of the flow regime, whether it's laminar or turbulent, right?
Exactly! Lower Reynolds numbers indicate laminar flow, while higher numbers signify turbulence. So understanding the drag coefficient helps in optimizing design!
Pressure Drag
Unlock Audio Lesson
Let's discuss pressure drag now. What do you think contributes to pressure drag in a fluid?
It’s related to the shape of the object, right? Like how air separates from a surface.
Correct! Pressure drag increases with flow separation, creating low-pressure areas behind the object. Can anyone give me an example of objects where we want to minimize pressure drag?
Like cars and airplanes — they need streamlined shapes.
Exactly! Streamlined shapes help reduce pressure drag, making these vehicles more fuel-efficient.
Application of Drag Concepts
Unlock Audio Lesson
How are we using the principles of drag in sports design and engineering?
Designing golf balls with dimples helps reduce drag!
Fantastic! The dimples create turbulence, which helps keep the airflow attached to the ball longer. Thus, reducing pressure drop. Can you think of any non-aerodynamic applications?
Tall buildings! We need to minimize wind resistance during bad weather.
Absolutely! Understanding drag helps in designing resilient structures. Remember, engineers should always consider flow effects to optimize designs.
Complex Interactions of Drag and Lift
Unlock Audio Lesson
In addition to drag, lift plays a crucial role. What defines lift in this context?
The upward force caused by pressure differences above and below an object.
Exactly! Lift works in conjunction with drag to determine the object's trajectory. How can we engineer for both?
By shaping the object to maximize lift while minimizing drag?
Spot on! Engineers balance these forces to achieve efficient designs, whether in vehicles, aircraft, or sports gear.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we discuss the fundamental principles underlying friction and pressure drag in fluid dynamics. We explain how these forces act upon objects moving through fluids, their dependence on surface characteristics and shapes, and the significance of drag coefficients in various applications, including vehicles and sports equipment.
Detailed
Detailed Overview of Friction and Pressure Drags
Introduction
In fluid mechanics, drag is a force exerted by a fluid on an object moving through it, with two primary components: friction drag and pressure drag. This section explores these components in detail.
Friction Drag
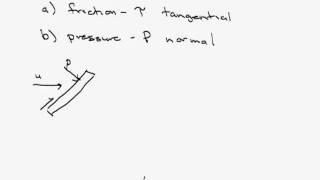
Friction drag is caused by the viscous effects of the fluid and the interaction between the fluid particles and the surface of the object. Known as skin friction, it arises due to boundary layer formations and can be influenced by the surface roughness of the object. The primary influencing factor is the dynamic viscosity of the fluid, and it is generally expressed mathematically in relation to the shape and size of the object.
Coefficient of Friction (Cd)
The drag force can be represented as:
$$ F_d = rac{1}{2} C_d \cdot \rho \cdot v^2 \cdot A $$
Where:
- $F_d$ is the drag force,
- $C_d$ is the drag coefficient,
- $
ho$ is the fluid density,
- $v$ is the flow velocity,
- $A$ is the reference area.
The coefficient of friction varies with different conditions such as Reynolds numbers, surface textures, and flow regimes (laminar vs turbulent).
Pressure Drag
Pressure drag arises due to differences in pressure on different sides of the object as the fluid flows around it. This difference is influenced by the object's shape and orientation with respect to the flow. Objects that separate the flow result in larger areas of low pressure behind them, leading to increased pressure drag.
Relationship with Flow Characteristics
The combination of friction and pressure drag can be crucial when designing vehicles, buildings, and various equipment to enhance performance and efficiency. Factors warranting consideration include environmental conditions and the object's geometric configurations.
Applications
The concepts of drag are crucial in various fields, from aerodynamic designs in vehicles and airplanes to optimizing sports equipment for performance. Understanding both components is essential for engineers and designers aiming to minimize drag and enhance efficiency.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Drag
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at the drag, it is a very simple definitions as you can understand it that is a force flowing fluid exerted on a body in the flow direction is called the drag.
Detailed Explanation
Drag is defined as the force exerted by a fluid (like air or water) on an object moving through it. This force opposes the motion of the object and acts in the direction of the flowing fluid. Think of it as resistance that slows down the object due to the fluid it travels through.
Examples & Analogies
Imagine riding a bicycle against the wind. The air pushes against you, making it harder to pedal forward. This force exerted by the air is similar to drag. The faster you go, the more wind (fluid) pushes against you, increasing the drag force.
Lift Force and Flow Separation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But you have a lift force you have a drag force. The component of the pressures and the wall strips in the direction normal to the flow tend to move the body in that direction.
Detailed Explanation
Lift is the force that acts perpendicular to the flow of the fluid, allowing objects like airplane wings to rise. It results from the pressure difference between the upper and lower surfaces of the wing. Flow separation occurs when the smooth flow of fluid is disrupted, leading to turbulence, which can dramatically affect lift and drag.
Examples & Analogies
Think of a bird flying. As its wings cut through the air, the shape of its wings creates a pressure difference: lower pressure on the top of the wing and higher pressure beneath it. This difference generates lift, enabling the bird to soar. If the bird's wing position caused the airflow to separate, it would lose lift, akin to a car losing traction on a slick road.
Coefficient of Drag
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So the basics of this coefficient drags we can get it from experiment basically conducting wind tunnel test or we can do numerical experiment.
Detailed Explanation
The coefficient of drag (Cd) is a dimensionless value that helps quantify the drag or resistance experienced by an object in a fluid. It is determined through experimental setups like wind tunnel tests, where the effects of various shapes and sizes are studied to observe how they alter the drag force experienced by an object.
Examples & Analogies
For example, when designing a new car, engineers use wind tunnels to model airflow around the vehicle. By changing the car's shape, they can measure how much drag it experiences. The goal is to design a shape with a low Cd, making the car more fuel-efficient while cruising.
Influence of Shape on Drag and Lift
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This drag and lift coefficients are primarily functions of shape of the body as I said it it also depends upon the Reynolds numbers and the surface roughness.
Detailed Explanation
The drag and lift coefficients greatly depend on the shape of the object moving through a fluid (like a balloon vs. a flat plate). Objects that are smooth and streamlined, like a teardrop, will have lower drag coefficients. Meanwhile, the Reynolds number identifies the flow characteristics (laminar or turbulent) around the object, and surface roughness (like the texture of a basketball) can affect how smoothly fluid flows around it.
Examples & Analogies
Consider a penguin sliding on ice. Its streamlined body causes it to glide easily with minimal drag, allowing it to move quickly with little resistance. Now picture a bulky box being pushed through water; it likely faces much more drag due to its unwieldy shape and rough surfaces.
Friction Drag vs. Pressure Drag
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As I said, that part of drag directly from the wall shear stress which is called skin friction drag since it is caused by the boundary layer formations.
Detailed Explanation
Friction drag occurs due to the contact between the fluid and the surface of the object. This is influenced by shear stress at the surface. In contrast, pressure drag arises from differences in pressure on opposite sides of an object, depending on its shape and the fluid flow direction. Together, these components help explain the total drag experienced by an object.
Examples & Analogies
Imagine swimming in a pool. When you press your hand against the water (friction drag), the smoothness or roughness of your hand affects how easily you can slice through. If you suddenly change to a wider arm position (increasing pressure drag), the additional water resistance slows you down significantly!
Design Considerations for Drag
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we can look at this elementary geometry and you can understand it that which one will give a minimum Cd values.
Detailed Explanation
When designing structures (like tall buildings), understanding how to minimize drag forces impacts safety and performance. Engineers can select shapes (square, circular) based on the expected wind speed. Properly selecting these geometric forms can result in lower drag coefficients, thereby improving stability during high winds.
Examples & Analogies
Think about designing a windmill. Its blades need to be streamlined to capture wind effectively while minimizing drag. If the blades are too bulky or oddly shaped, they may not rotate efficiently, reducing energy generation compared to a sleek, well-designed blade.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Friction Drag: Resistance caused by viscous forces at the surface of an object.
-
Pressure Drag: Resulting from pressure differences acting on an object.
-
Coefficient of Drag: A metric to quantify drag effects relative to dynamic conditions.
-
Reynolds Number: Determines the state of fluid flow around a body; crucial for understanding drag behavior.
-
Boundary Layer: Region where viscous effects dominate; critical for analyzing drag.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Cyclists lean forward to reduce drag by minimizing their frontal area.
-
Modern race cars have streamlined designs to minimize both friction and pressure drag.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Drag in the air and water flows, friction slows, pressure grows!
📖 Fascinating Stories
-
Imagine a cyclist tiptoeing against the wind, the tighter they tuck, the faster they spin! Friction in focus, pressure’s the foe, together they make a drag force that grows.
🧠 Other Memory Gems
-
Friction's Force Creates Resistance (FFCR) - Remember the importance of surface and viscosity!
🎯 Super Acronyms
DRAFT - Drag, Resistance, Airflow, Friction, Turbulence – key concepts in drag dynamics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Friction Drag
Definition:
The drag force resulting from the interactions between a fluid and the surface of an object due to viscosity.
-
Term: Pressure Drag
Definition:
The drag force caused by the pressure difference between the front and rear of a moving object in a fluid.
-
Term: Drag Coefficient (Cd)
Definition:
A dimensionless number describing the drag force relative to the fluid dynamics at play.
-
Term: Reynolds Number
Definition:
A dimensionless value that represents the ratio of inertial forces to viscous forces in fluid flow, indicating whether the flow is laminar or turbulent.
-
Term: Boundary Layer
Definition:
The thin layer of fluid in immediate contact with a surface, where effects of viscosity and friction are significant.