Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Drag Force
Unlock Audio Lesson
Good morning, everyone! Today, we’re starting with drag force, which is defined as the force exerted by the fluid on an object moving through it. Can anyone tell me how we calculate drag force?
Is it related to the fluid density and velocity?
Exactly! The formula is \( F_D = \frac{1}{2} \rho v^2 C_D A \). Here, \( A \) is the frontal area of the object. Can anyone explain what each term stands for?
Sure! \( \rho \) is the density of the fluid, \( v \) is the velocity, and \( C_D \) is the drag coefficient.
Great job! Remember, the drag coefficient varies based on the shape and orientation of the object, which we will explore shortly. Let’s recap: Drag force is influenced by fluid density, velocity, and object shape.
Exploring Lift Force
Unlock Audio Lesson
Now, let’s talk about lift force, which acts perpendicular to the flow direction. Why do we think lift is crucial for airplanes?
Because it helps the plane rise and stay in the air!
Right! Lift force can be calculated in a similar manner to drag. So, how does the lift force relate to different speed conditions?
Higher speeds increase lift, which is essential for takeoff.
Good observation! Remember, optimizing the shape of an airplane wing can maximize lift while minimizing drag. So, to summarize: lift must overcome weight and is essential for flight.
Drag and Lift in Cycling
Unlock Audio Lesson
Let’s pivot to cycling! How do professional cyclists minimize drag?
They wear tight clothing and lower their body position!
Right! By reducing their frontal area and streamlining their position, they decrease their drag coefficient, allowing them to achieve higher speeds.
How does that affect their performance during races?
Excellent question! Reduced drag allows cyclists to maintain speed with lower energy expenditure which is crucial in competitive racing.
Wind Turbines and Drag Coefficient
Unlock Audio Lesson
Switching gears, how are drag coefficients important in wind turbine design?
They need to minimize drag to extract as much energy from the wind as possible!
Correct! Designers must consider both lift and drag to maximize efficiency. What happens if a turbine has a high drag coefficient?
It won't capture enough energy and will be less efficient?
Exactly! So, to summarize: understanding lift and drag coefficients is key in engineering applications like cycling and wind turbine design.
Pressure and Friction Drag
Unlock Audio Lesson
Finally, let’s differentiate between pressure drag and friction drag. Does anyone know how these two types of drag differ?
Pressure drag is due to pressure differences around an object, while friction drag is due to the fluid's viscosity?
Perfectly stated! Friction drag acts along the surface of an object, and pressure drag is often more significant in shapes with large frontal areas.
Is there a way to reduce both types of drag in designs?
Indeed! Streamlined designs help minimize both friction and pressure drag. To summarize: pressure drag relates to shape while friction drag relates to surface texture.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores the principles of lift and drag coefficients, explaining how they are influenced by factors such as shape, orientation, and fluid mechanics principles. It provides examples from cycling, aerodynamics, and sports to illustrate real-world applications and the importance of minimizing drag forces to optimize performance.
Detailed
Detailed Summary
This section provides an in-depth analysis of the coefficients of lift and drag, key concepts in fluid mechanics essential for predicting how objects behave as they move through fluids. The coefficients are influenced primarily by the geometry of the objects, the fluid's density, and the speed of flow.
Key Concepts Discussed:
- Drag Force: Defined as the resistance force acting opposite to the direction of motion of an object through a fluid. It can be computed using the formula:
\[ F_D = \frac{1}{2} \rho v^2 C_D A \]
where \( F_D \) is drag force, \( \rho \) is fluid density, \( v \) is velocity, \( C_D \) is the drag coefficient, and \( A \) is the frontal area.
- Lift Force: The force acting perpendicular to the flow direction, assisting objects like airplane wings in achieving flight. The relationship is similar to drag but focuses on generating lift, often to overcome the object's weight.
- Experimental and Numerical Methods: The section emphasizes practical approaches—wind tunnel tests and computational fluid dynamics software—which allow engineers to determine drag and lift coefficients efficiently.
- Real-World Applications: Examples from cycling, swimming, and wind turbine design illustrate the necessity for minimizing drag to improve efficiency and maximize performance.
The need for optimizing the shape, position, and orientation of objects in various fields of engineering is crucial to managing the forces of lift and drag.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Drag and Lift
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The drag force is defined as a function of half rho v squared, multiplied with a Cd, which is called the coefficients of drag, into A, the frontal area.
Detailed Explanation
The drag force experienced by an object moving through a fluid (like air) can be calculated using the formula F_d = 0.5 * ρ * v² * C_d * A. Here, ρ is the density of the fluid, v is the velocity of the object, C_d is the drag coefficient which varies with the shape and orientation of the object, and A is the frontal area (the area projected in the direction of the flow). This formula shows that the drag force increases with the speed of the object and depends on its shape through the drag coefficient.
Examples & Analogies
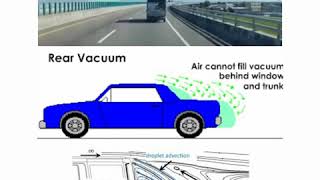
Think of a car speeding on the highway: the faster it goes, the more air resistance (drag) it encounters. Engineers design cars with smoother shapes to reduce drag and improve fuel efficiency.
Understanding the Drag Coefficient (C_d)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The drag coefficient (C_d) can be obtained from experiments such as wind tunnel tests or numerical simulations. It is a function of the fluid's velocity, density, frontal area, shape, size, and orientation.
Detailed Explanation
The drag coefficient (C_d) quantifies how well an object can move through a fluid. It is derived through experimental methods, such as placing a model in a wind tunnel where the airflow is analyzed. The coefficient can change based on the object's shape, the speed of the fluid, and the density of the fluid. A lower C_d indicates that an object faces less resistance, which is ideal for designs like cars and airplanes.
Examples & Analogies
Imagine two cyclists: one is upright and exposed to more air resistance, while the other leans forward to minimize frontal area. The second cyclist has a lower drag coefficient, allowing them to go faster with the same amount of effort.
Factors Influencing Drag and Lift
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
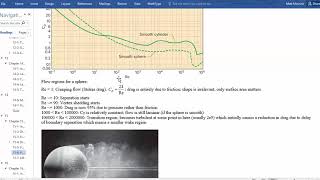
The drag and lift coefficients are primarily functions of the shape of the body, Reynolds numbers, and the roughness of its surface.
Detailed Explanation
Reynolds number is a dimensionless quantity used to predict flow patterns in different fluid flow situations. It considers factors like the object's size, the fluid's velocity, and its viscosity. A smooth surface will have a different drag and lift behavior compared to a rough one; for instance, surfaces that are more textured may increase drag in certain conditions by disrupting smooth airflow. Understanding how these factors interrelate is crucial for engineers designing efficient vehicles and structures.
Examples & Analogies
Consider a golf ball with dimples compared to a smooth ball: the dimples create turbulence in the air, allowing the ball to stay in the air longer and travel further. This is a practical application of manipulating drag and lift through shape and surface characteristics.
Summary of Drag and Lift Applications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applications of drag and lift concepts can be seen in various fields, such as in the design of wind turbines and racing bikes.
Detailed Explanation
Understanding drag and lift is essential in multiple industries. For example, in wind turbine design, engineers must ensure that blades efficiently capture wind to generate power, which involves optimizing lift. Similarly, cyclists in competitive racing aim to reduce drag to maintain speed, improving their performance through body positioning and equipment design. By grasping these concepts, students can appreciate their real-world implications.
Examples & Analogies
Think about airliners, where the wing shape is meticulously designed to create lift without excessive drag, allowing planes to soar efficiently at high speeds. This design is crucial for fuel economy and safety.
Exploring Terminal Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Dust particles can reach a terminal velocity where the drag force balances the weight and buoyancy forces acting on them.
Detailed Explanation
Terminal velocity occurs when the downward force of gravity (weight) equals the upward drag force and buoyancy, resulting in zero net acceleration. For small particles, as they fall through the air, they accelerate until the drag force opposing their motion equals the gravitational pull, leading them to fall at a constant speed. This principle is significant not only in meteorology but also for understanding how various materials interact with fluids.
Examples & Analogies
Picture a feather falling through the air: at first, it falls slowly, but as it gathers speed, it eventually stops accelerating when the air resistance matches its weight, gliding gently down to the ground.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Drag Force: Defined as the resistance force acting opposite to the direction of motion of an object through a fluid. It can be computed using the formula:
-
\[ F_D = \frac{1}{2} \rho v^2 C_D A \]
-
where \( F_D \) is drag force, \( \rho \) is fluid density, \( v \) is velocity, \( C_D \) is the drag coefficient, and \( A \) is the frontal area.
-
Lift Force: The force acting perpendicular to the flow direction, assisting objects like airplane wings in achieving flight. The relationship is similar to drag but focuses on generating lift, often to overcome the object's weight.
-
Experimental and Numerical Methods: The section emphasizes practical approaches—wind tunnel tests and computational fluid dynamics software—which allow engineers to determine drag and lift coefficients efficiently.
-
Real-World Applications: Examples from cycling, swimming, and wind turbine design illustrate the necessity for minimizing drag to improve efficiency and maximize performance.
-
The need for optimizing the shape, position, and orientation of objects in various fields of engineering is crucial to managing the forces of lift and drag.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A cyclist leans forward to reduce their frontal area, thus decreasing their drag coefficient and allowing them to attain maximum speed.
-
In wind turbines, the blade angles are designed to maximize lift while minimizing drag using the principles discussed.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When drag is high, you can't fly; reduce that force to soar the sky!
📖 Fascinating Stories
-
Imagine a cyclist racing against the wind. As they lean forward, they slice through the air more smoothly, allowing them to speed past their competitors—this is how drag impacts performance!
🧠 Other Memory Gems
-
DOL - Drag Opposes Lift: Remember that drag and lift are opposing forces in motion.
🎯 Super Acronyms
LIFT - Lift Increases From Thrust
- When velocity increases
- lift should follow for flight.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Drag Force
Definition:
The resistance force exerted by a fluid on an object moving through it, calculated with the formula \( F_D = \frac{1}{2} \rho v^2 C_D A \).
-
Term: Lift Force
Definition:
The force acting perpendicular to the flow direction that helps objects rise, crucial for applications like airplanes.
-
Term: Drag Coefficient (C_D)
Definition:
A dimensionless number that quantifies drag or resistance of an object in fluid motion, influenced by shape and surface characteristics.
-
Term: Frontal Area (A)
Definition:
The projected area of an object in the direction of flow, which affects the drag force experienced.
-
Term: Boundary Layer
Definition:
The thin layer of fluid in the immediate vicinity of a bounding surface where the effects of viscosity are significant.