Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydraulic Radius
Unlock Audio Lesson
Good morning, class! Today, we're going to dive into the concept of hydraulic radius. Can anyone tell me what they think it measures?
Is it related to the flow of water in rivers or channels?
Exactly! The hydraulic radius is the ratio of the cross-sectional area of flow to the wetted perimeter of the channel. Specifically, it helps us understand how water flows in different channel shapes.
So, how is it calculated?
Great question! It's calculated using the formula R = A / P, where R is the hydraulic radius, A is the area of flow, and P is the wetted perimeter. Can anyone remind me what the wetted perimeter refers to?
I think it's the part of the channel that is in contact with the water, right?
Correct! It's essential to focus on the part of the channel that affects water flow. As we learn, different shapes will give us different hydraulic radii, which in turn informs how we analyze the flow.
Why would a wider channel matter for the hydraulic radius?
When we consider wider channels, the hydraulic radius can approach the flow depth, which impacts our calculations and understanding of flow dynamics. Let's summarize what we've covered today!
Calculation and Significance
Unlock Audio Lesson
Now, let's get into how we actually calculate the hydraulic radius using different channels, starting with a rectangular channel. If the width of the channel is b and the flow depth is y, what would be the area A?
The area would be b times y, right?
Exactly! And what's the wetted perimeter P for a rectangular channel?
It would be b plus 2y because we add the two depths on the sides.
Correct! So, the hydraulic radius would be R = (b * y) / (b + 2y). As you can see, the hydraulic radius can change based upon the ratio of width to depth. What happens when y becomes much smaller compared to b?
The radius would approach the depth, I think.
Right! This shows us that in wider channels, our calculations can simplify considerably. Now, let’s summarize our key points.
Hydraulic Radius and Flow Behavior
Unlock Audio Lesson
Let's connect the concepts we've learned about hydraulic radius with actual flow behavior. Why do you think understanding R helps us in managing open channel flows?
I guess it allows us to predict how water will flow in channels better.
Exactly! It helps us predict the velocity and energy loss, which are critical for designing efficient drainage systems or canals. Can anyone tell me how hydraulic radius might be used in a real-world scenario?
Perhaps in designing irrigation canals?
Yes, precisely! Designers can calculate hydraulic radius to optimize the flow rate in different channel shapes. Let’s review the essential concepts before we wrap up.
Comparative Analysis with Pipe Flow
Unlock Audio Lesson
Now, let's shift our focus slightly. We talked about open channels, but how do you think hydraulic radius compares to the diameter of circular pipes?
I think hydraulic radius would be a more versatile measurement since it applies to different channel shapes.
Absolutely! In pipe flow, we typically use diameter, whereas for open channels, we have hydraulic radius. Does anyone remember the critical Reynolds number for open channel flow?
Isn't it around 500?
Correct! And this shows how hydraulic radius helps determine flow regimes too. Great engagement! Let's summarize what we learned today.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section elucidates the hydraulic radius which is the ratio of the area of flow to the wetted perimeter. The discussion includes various flow cross sections such as rectangular and trapezoidal channels and emphasizes the application of hydraulic radius in analyzing open channel flow. It concludes with the significance of hydraulic radius in comparing open channel flow to pipe flow.
Detailed
Hydraulic Radius Concept
The hydraulic radius is a foundational concept in understanding open channel flow. It is defined as the ratio of the cross-sectional area of flow (A) to the wetted perimeter (P). This section emphasizes the importance of this ratio in analyzing the behavior of fluids in open channels.
Key Points:
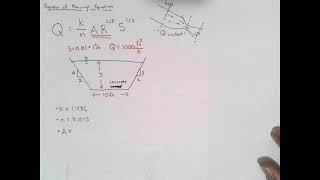
- Definition: The hydraulic radius (R) is calculated as:
R = A / P
where A is the cross-sectional area of flow and P is the wetted perimeter.
- Significance: The hydraulic radius provides insights into the flow characteristics, particularly in comparing different channel geometries. For instance, in rectangular channels, as the width becomes much larger than the depth, the hydraulic radius approaches the flow depth, emphasizing that the depth significantly influences flow resistance.
- Applications: Understanding hydraulic radius is crucial for calculating flow velocities, determining flow rates, and conducting energy loss analyses in open channels. It serves as a vital parameter in the Reynolds number calculations, especially when comparing with pipe flows.
This concept lays the foundation for further discussions on classifications of open channel flow and the dynamics of fluid behavior in both natural and artificial channels.
Youtube Videos
![[HYDRAULIC #1] Concept of Hydraulic Mean Depth and Hydraulic Radius and their Differences](https://img.youtube.com/vi/SON_Hh9Eibk/mqdefault.jpg)
![Open Channel Flow - 6 [Flow Area A, Wetted Perimeter P Hydraulic Radius R, and Hydraulic Depth D]](https://img.youtube.com/vi/lyecuNbxlAs/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Hydraulic Radius
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we have introduced a new concept to look at that one is called hydraulic radius because as I sketching these different cross sections. In pipe flow, you may have the circular or this square pipe flow but in natural rivers, in case of different canal structures or drainage structures. So we need to have a hydraulic radius concept.
Detailed Explanation
The hydraulic radius is a crucial concept in fluid mechanics, especially in the study of open channel flow. It serves as a simplified measure to understand how fluid behaves in different geometrical configurations. The hydraulic radius (R) is defined as the cross-sectional area (A) of flow divided by the wetted perimeter (P) that is in contact with the fluid. In essence, R = A / P. This ratio helps in characterizing the flow's efficiency and energy loss, making it easier to analyze various flow scenarios.
Examples & Analogies
Imagine a wide river compared to a narrow stream. The river (wide flow area) allows water to flow more efficiently due to its larger area compared to the smaller perimeter of the shallow stream. This difference can be captured using the hydraulic radius, which will be larger for the river, indicating a more efficient flow.
Defining Hydraulic Radius
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So area is the area of the flow cross sections okay that is what is it is equivalent to a meter dimensions okay you can just put it okay is a radius we define it A by P. So what does mean by that I just have a very simple example that if I have a rectangle channels y is my depth and b is my width okay. So area will be simple things area will be b into y okay simple geometry.
Detailed Explanation
For rectangular channels, the area (A) can be calculated as width (b) multiplied by depth (y) of the channel: A = b * y. The wetted perimeter (P) for a rectangular channel would be the width of the bottom (b) plus twice the depth (2y) since the water is in contact with both the sides of the channel. Hence, P = b + 2y. The hydraulic radius is consequently calculated using R = A / P.
Examples & Analogies
Think of a rectangular swimming pool. The area of the water surface represents the flow area, and the edges of the pool that touch the water are like the wetted perimeter. To understand how efficiently the pool can drain, you can think about dividing the area of the water surface by the length of the walls submerged in water—this gives us the hydraulic radius, helping us with calculations for water flow.
Effects of Channel Geometry
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So hydraulic radius will be the A by P which means the b by y b plus 2y okay so b by y by b plus 2y. if y is much much less than the b as compared to a river systems okay b is much larger maybe around 200 meters or 300 meters y will be 3 meter or 4 meters if you have that the conditions.
Detailed Explanation
This chunk discusses how the hydraulic radius changes with channel geometry. When the depth (y) is significantly less than the width (b), the hydraulic radius closely approximates the depth. For instance, if you have a river that is 200 meters wide but only 3 meters deep, the hydraulic radius (R) will be nearly equal to the depth (y), simplifying calculations and analyses in open channel flow scenarios.
Examples & Analogies
Consider a small stream running next to a much wider river. If both have a similar depth but the river is much wider, the flow dynamics in the river will behave significantly differently due to this increased width. This relationship helps civil engineers predict and manage water flow in different environments.
Hydraulic Radius in Circular and Trapezoidal Channels
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So it is a very simple things just to have to understand that to estimate the area, flow, perimeters and estimate the hydraulic radius. okay so with this let me I conclude today lecture.
Detailed Explanation
In circular and trapezoidal channels, the calculation of the hydraulic radius involves understanding their specific geometries. For circular pipes, one would measure the angle of submersion and calculate the wetted perimeter, while trapezoidal channels require accounting for the slopes of the sides. This versatility in applying the hydraulic radius concept to different channel shapes allows engineers to analyze water flow effectively across diverse scenarios.
Examples & Analogies
Imagine a circular pipe under a city that transports water. The engineers need to calculate how effectively water can flow through it. Here, they would use the hydraulic radius to determine how much area is available for flow versus the perimeter that affects this flow. The same consideration applies to a trapezoidal drainage channel used in landscaping.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydraulic Radius: The ratio of area to wetted perimeter, crucial for analyzing flow.
-
Wetted Perimeter: The length in contact with water, important for calculating hydraulic radius.
-
Reynolds Number: A critical measure for understanding flow regimes in both open channels and pipes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a rectangular channel with a width of 5 meters and a depth of 2 meters, the hydraulic radius would be R = (5 * 2) / (5 + 4) = 10/9 m.
-
For a trapezoidal channel, calculating the area and wetted perimeter requires different lengths, emphasizing the versatility of hydraulic radius across different channel shapes.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Radius high or radius low, flow that's smooth will surely show.
📖 Fascinating Stories
-
Imagine a river that wants to flow wide. The more space it has, the deeper it glides. So when we measure, let’s keep that in mind—wetted perimeter and area combined!
🧠 Other Memory Gems
-
A P-tion for radius: Remember A over P to find R!
🎯 Super Acronyms
RAP
- Radius from Area and Perimeter.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydraulic Radius
Definition:
The ratio of the cross-sectional area of flow to the wetted perimeter of a channel, used to analyze fluid flow.
-
Term: Wetted Perimeter
Definition:
The length of the boundary of a channel that is in contact with the water.
-
Term: Crosssectional Area
Definition:
The area of the flow at a particular point across a channel.
-
Term: Flow Rate
Definition:
The volume of fluid that passes through a cross-section of a channel per unit time.
-
Term: Reynolds Number
Definition:
A dimensionless quantity used to predict flow patterns in different fluid flow situations, calculated using properties of fluid flow.