Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to No Slip Boundary Conditions
Unlock Audio Lesson
Today, we will discuss the no slip boundary condition, which is foundational in understanding how fluids behave near surfaces. Can anyone explain what you think the no slip condition entails?
Is it about the fluid sticking to the boundary?
Exactly! The fluid velocity at the boundary where it meets the solid surface is zero. This is crucial because it implies that there will be a velocity gradient in the fluid layer close to the boundary.
Does that mean the fluid starts moving slower near the boundary?
Yes, that's correct! This differential motion is what gives rise to shear stress in the fluid near the wall. Remember, this is key to understanding turbulence and flow dynamics. It's like a river where the water at the edges moves slower due to contact with the riverbed.
Why is it important to know the velocity is zero at the boundary?
Understanding this allows us to analyze the forces acting on the fluid, specifically the friction force and the gravitational forces. It simplifies our calculations significantly.
So, it helps determine how fast the water flows?
Exactly! We often need to calculate how quickly the water can move through different types of channels.
In summary, the no slip boundary condition means the fluid velocity at the wall is zero, leading to a velocity gradient which is fundamental for analyzing fluid flow.
Velocity Distribution in Open Channel Flow
Unlock Audio Lesson
Now let's talk about velocity distribution. How do you think the no slip condition affects how fast water moves throughout a channel?
I think the velocity should increase as we move away from the boundary.
That's exactly right! Near the boundary, the velocity is zero, but it increases as we move toward the center of the flow. Does anyone remember how we express that gradient?
I think it forms a parabolic shape?
Good memory! Typically, the velocity profiles can take a parabolic shape, especially in laminar flow. In turbulent flow, the profile becomes more complex but still retains that fundamental idea of lower velocities near the boundaries.
So, what does maximum velocity tell us?
The maximum velocity occurs typically about 0.2 times the flow depth from the surface. This relationship helps us design structures and predict flow behavior.
To summarize, the no slip boundary condition leads to a velocity distribution where fluid speed increases as you move from the boundary into the center of the channel, creating a velocity profile important for analyzing flow.
Classification of Open Channel Flow
Unlock Audio Lesson
Let's shift our focus to the classifications of open channel flow. Can anyone mention a type of flow we've learned about based on velocity?
Is it uniform flow?
Yes! Uniform flow remains constant in depth, velocity, and slope along the length of the channel. What do you think conditions lead to a uniform flow?
It probably occurs when there's no net acceleration?
Exactly! Uniform flow occurs when the forces acting are balanced. What about gradually varied flow?
That must be when flow parameters change gradually over a distance?
Spot on! And what can you tell me about rapidly varied flow?
I think that's when there's a quick change in flow parameters?
Correct! Rapidly varied flow happens when the flow depth or slope changes sharply, often leading to structures like hydraulic jumps. Remember that understanding these classifications can help us design better hydraulic systems.
In summary, we have uniform, gradually varied, and rapidly varied flows, each reflecting how flow characteristics can change along a channel.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section focuses on the no slip boundary condition, which states that the velocity at the boundary is zero due to the fixed nature of the boundary. This leads to a simplified flow analysis where gravity and friction forces dominate. The section also covers velocity distribution and classifications of flow, emphasizing steady, unsteady, uniform, and varied flows.
Detailed
In this section, we explore the foundational concept of no slip boundary conditions, which states that the fluid velocity at a solid boundary is zero. This principle is crucial for analyzing fluid flows in open channels, where fluids flow over a free surface and experience gravity and friction forces. The pressure at the free surface is atmospheric, and the only forces acting on the fluid are gravity and friction, leading to simpler governing equations for flow dynamics. We discuss how velocity distributions typically show that maximum velocities occur away from the boundary and near the free surface. This section also introduces flow classifications, distinguishing between uniform, gradually varied, and rapidly varied flows in open channels. Understanding these concepts lays the groundwork for further discussions on flow energy, hydraulic radius, and various applications in civil engineering and fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding No Slip Boundary Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
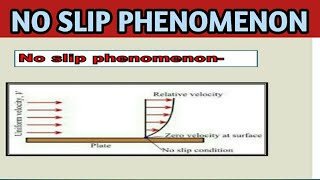
The no slip boundary conditions imposes us the velocity near to this boundary will be 0. The velocity near to the boundary because of no slip boundary conditions the boundary is fixed at the locations. So, the velocity becomes 0.
Detailed Explanation
No slip boundary conditions mean that at the very edge or boundary of a fluid flow (like the walls of a canal or a riverbed), the speed of the fluid is zero. This happens because the fluid sticks to the surface due to viscosity, a property of the fluid that causes it to resist flow. When we say that 'the velocity becomes 0', we are indicating that right at the interface between the fluid and the surface, there is no movement. As we move away from the boundary into the fluid, the velocity of the fluid increases.
Examples & Analogies
Imagine you are swimming in a pool. When you try to push your hand against the side of the pool, your hand does not move; it sticks to the wall. In this situation, the water right next to the wall (boundary) is also stationary because it clings to the wall. This is similar to how the fluid behaves near any solid boundary.
Impact on Velocity Distribution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
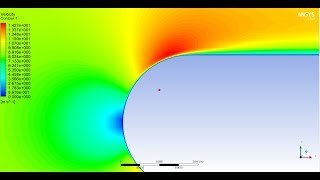
Since it is a 0, that means I can draw the velocity distributions velocity contours okay iso velocity contours I can draw.
Detailed Explanation
Due to the no slip condition, we can depict how fluid velocity changes across different layers of flow. The velocity distribution shows how fast the fluid is moving at different points above the boundary. Close to the boundary, the velocity is 0, and as you move upward through the fluid, the velocity increases. This creates a gradient of velocities, which we can represent with velocity contours. These contours help illustrate how the speed of the fluid varies across the flow area.
Examples & Analogies
Think about stirring a smoothie in a blender. The fruit stuck to the bottom remains still because of the walls of the blender. As you move up, the fruity mixture flows faster and creates a swirling effect. If we could visualize the speed of the mixture, we would see layers of different speeds, with the bottom layer (near the wall) being stationary.
Two Forces in Open Channel Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look at more introductions levels we are talking about also we will talk about the classifications of open channel flow, hydraulic radius for some common sections and we talk about the wave speed and flow power numbers.
Detailed Explanation
In open channel flow, there are two main forces acting on the fluid: the gravitational force which pulls the fluid downwards, and the frictional force that resists the flow due to contact with the channel bed and sides. The gravitational force is what drives the flow down the slope, while friction slows it down. Understanding these forces is crucial for analyzing the behavior of fluid flow in channels, as they determine how fast the fluid moves and how much energy is lost due to friction.
Examples & Analogies
Imagine a water slide. Gravity pulls you down, making you move fast, but as you slide against the surface, you feel some resistance due to friction. The steeper the slide, the faster you go, but the rougher the slide surface, the slower you will slide down. Similarly, in an open channel, the flow speed varies based on the angle of the channel (slope) and the roughness of its bottom and sides.
Pressure Conditions at Free Surface
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
At these locations pressure is equal to atmospheric pressures because it is a free surface.
Detailed Explanation
In an open channel flow, at the free surface where the fluid meets the air, the pressure equals atmospheric pressure. This is different from flows in closed systems (like pipes) where pressure can be higher than atmospheric. At the free surface, the weight of the water above creates pressure, but at the surface itself, the pressure equalizes with the surrounding atmosphere. This is an important factor that influences fluid behavior, especially in calculating forces and pressures acting through the fluid.
Examples & Analogies
Consider a glass filled to the brim with water. The water at the very top of the glass is at atmospheric pressure, just like the air around it. If you dip a straw into the glass, the water inside the straw is still affected by the atmospheric pressure at the top surface of the glass, which ultimately determines whether water stays in the straw or falls out.
Concepts of Flow Classification
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We classify the flow into three categories: subcritical, critical, and supercritical.
Detailed Explanation
Flow classification in open channels helps us understand how the fluid behaves under various conditions. Subcritical flow occurs when the flow speed is less than the wave speed, leading to smooth, steady flow. Critical flow happens at the transition point between subcritical and supercritical, where the flow speed equals wave speed. Supercritical flow, on the other hand, occurs when the flow speed exceeds wave speed, leading to rapid and turbulent conditions. These classifications allow engineers to predict how water will move and interact with its environment.
Examples & Analogies
Imagine a river flowing gently – that's subcritical flow. If you dropped a pebble in such water, the ripple would travel outward slowly. When the water reaches a rapid drop-off where it flows down quickly, it has transitioned to supercritical flow. If you tossed the same pebble at this point, the ripples would move much faster and more chaotically compared to the earlier gentle flow.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
No Slip Boundary Condition: Statement that velocity at a boundary is zero.
-
Velocity Gradient: Change in velocity from the boundary to the center of the flow.
-
Uniform Flow: A state where velocity and depth remain constant.
-
Gradually Varied Flow: A classification where flow parameters change slowly over distance.
-
Rapidly Varied Flow: A classification where flow parameters change quickly over short distances.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a river, the water flows faster in the center than at the edges due to no slip boundary conditions.
-
When considering a hydraulic jump in a channel, water starts flowing rapidly followed by a sudden change in depth.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
A boundary so near, the water has fear, its velocity's slow, as it touches the toe!
📖 Fascinating Stories
-
Once upon a river, the king was crowned. The quicker the flow, the deeper the sound. But at the edges, the king lay still; that's where the no slip taught us its skill.
🧠 Other Memory Gems
-
Use the acronym 'SUN' to remember: S for Steady (flow), U for Uniform (flow), N for No slip (condition).
🎯 Super Acronyms
Remember 'FVS' - F for Friction, V for Velocity, S for Shear stress.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: No Slip Boundary Condition
Definition:
The condition in fluid dynamics where the velocity of fluid at a solid boundary is zero.
-
Term: Velocity Distribution
Definition:
The variation of velocity across the cross-section of a flowing fluid.
-
Term: Uniform Flow
Definition:
Flow in which the velocity, depth, and other parameters remain constant along the channel.
-
Term: Gradually Varied Flow
Definition:
Flow in which the parameters change gradually over a distance.
-
Term: Rapidly Varied Flow
Definition:
Flow in which the parameters change significantly over a short distance.