Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Open Channel Flow
Unlock Audio Lesson
Today, we are starting with open channel flow. Can anyone tell me what distinguishes open channel flow from pipe flow?
Open channel flow has a free surface, while pipe flow is enclosed.
Exactly! In open channel flow, the pressure at the free surface is atmospheric. This simplifies many calculations. Remember that the main forces acting here are gravity and friction.
What role does gravity play in this context?
Gravity drives the fluid movement in open channels, aiding in flow velocity, while friction counters this flow. These two forces balance out to determine the flow characteristics.
How does the velocity distribution look in open channels?
Great question! The velocity is highest at the surface and decreases towards the boundary due to friction. This creates a velocity profile that we can sketch using contours.
Can you explain what these contours represent?
Yes! Velocity contours represent lines of equal velocity in the flow. It's critical to understand these profiles for effective water management.
To summarize, open channel flow fundamentally differs from pipe flow due to its free surface, and the main forces involved are gravity and friction. The velocity profile is key in understanding how water moves in these channels.
Velocity Distribution Profiles
Unlock Audio Lesson
Now, let’s discuss velocity distribution profiles in more detail. What do you think happens to velocity as we move from the free surface downwards?
I think it decreases due to friction with the channel walls.
Correct! The maximum velocity is typically around 0.2 times the depth of the flow from the surface. This means that the highest velocities occur just beneath the free surface.
So, if the depth increases, does the velocity also increase?
Good observation! Yes, as depth increases, so does the cross-sectional area for flow, potentially increasing overall velocity, but the distribution profile still remains important.
Can you clarify how we could visualize these distributions?
Absolutely! By sketching velocity contours based on measured velocities, we can create a visual representation. I recommend practicing this by drawing these contours for different scenarios.
In summary, velocity tends to decrease with depth relative to the free surface, and we visualize this through contour sketches, which help in analyzing flow characteristics.
Practical Applications of Velocity Distributions
Unlock Audio Lesson
Let's connect what we've learned to real-world applications. Why do you think understanding velocity distributions is essential in civil engineering?
It helps in designing canals and drainage systems effectively.
Exactly! Proper design minimizes erosion and optimizes transport efficiency. Can someone explain how velocity distributions play a role in these designs?
By predicting how much water can flow through the channel without causing overflow or erosion.
Correct! Additionally, engineers need to ensure that friction losses are accounted for, which also come into play with velocity.
What about environmental impacts?
Excellent thought! Velocity distributions can influence sediment transport and aquatic habitats, requiring careful consideration in design.
In summary, understanding velocity distributions is vital for civil engineering applications, as it ensures efficient and environmentally-friendly water management.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Velocity distributions in open channel flow are critical for understanding fluid mechanics applications such as river systems and drainage networks. This section explores how velocity changes with depth and the implications of pressure and friction forces in analyzing these flows.
Detailed
Velocity Distributions in Open Channel Flow
In this section, we delve into the concept of velocity distributions within the context of open channel flow, a vital topic in fluid mechanics. Open channels, unlike closed pipe systems, have a free surface where pressure equals atmospheric pressure, simplifying analysis significantly. By applying the principles of mass conservation, linear momentum, and energy conservation, we gain insights into how velocity behaves in natural (like rivers) and artificial channels (like canals).
Key Points Covered:
- The foundational principles of fluid mechanics applied to open channel flow.
- The significance and effects of free surfaces on velocity distributions, highlighting how pressure remains atmospheric.
- The effects of gravity and frictional forces on fluid flow, eliminating surface pressure components in open channel analysis.
- The implications of no-slip boundary conditions that lead to zero velocity at the boundaries of the flow.
- The shapes and characteristics of flow in natural and man-made channels, defining the distinction between uniform and non-uniform flows.
Understanding these velocity distributions not only aids in effective open channel flow calculations but also informs the design and management of engineering solutions for water transport and drainage.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Velocity Distributions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
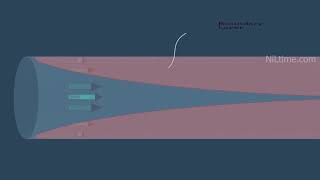
So since it is a 0 that means I can draw this the velocity distributions velocity contours okay iso velocity contours I can draw the velocity contours that means maybe this velocity is equal to 2 meter per second next maybe 1.5, 1, 0.5 meter per second. This is what the contours of equal velocities that is what you can be because near to the boundary velocity is 0. So you can have a velocity distribution like you can have a velocity for this case also you can have a velocity distributions like that is what I always encourage you to just draw the safe try to understand it how the velocity distributions are happening it okay.
Detailed Explanation
In open channel flow, the distribution of velocity can be visualized using contours known as iso-velocity contours. These contours represent lines connecting points of equal velocity at various depths of flow. Near the boundary of the channel, the velocity is zero due to the no-slip condition which states that fluid in contact with the boundary does not move. As you move away from the boundary into the main body of the flow, the velocity increases and can be represented through contours, which can help visualize flow characteristics clearly.
Examples & Analogies
Imagine watching a river flow. Right at the edge where the water meets the bank, the water is still – that's the 'no-slip' condition. As you look out towards the middle of the river, the water is moving swiftly. If you could draw lines connecting places that have the same speed, you would see those lines curving because the speed changes across the width and depth of the river.
Understanding the Concept of Hydraulic Radius
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, the basically we can have a different classifications of the flow we will discuss more details. why we need it subcritical supercritical and the flow conditions.
Detailed Explanation
The hydraulic radius is defined as the cross-sectional area of flow divided by the wetted perimeter. This concept is crucial in understanding how flow behaves in different conditions, such as subcritical (calm) and supercritical (fast-moving) flows. The hydraulic radius helps to calculate other parameters of flow in an open channel, making it easier for engineers to design channels and predict flow characteristics efficiently.
Examples & Analogies
Think of a garden hose; if you partially cover the end of the hose with your thumb, the speed of the water shooting out increases because the area the water can flow through is smaller. In open channel flow, wider or older infrastructures may behave differently than new, narrow ones. Understanding the hydraulic radius allows civil engineers to consider how changes in channel shape and size affect water flow, much like adjusting the nozzle on a hose.
Classification of Open Channel Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As we discuss very beginning of dimensional analysis we use the flow proud numbers for classifications of these like flow proud numbers if is equal to the 1 then is a critical if it is a greater than 1 is supercritical less than 1 is subcritical.
Detailed Explanation
Flow in open channels can be classified into three main categories based on flow velocity and gravitational effects: subcritical flow (less than critical speed), critical flow (at critical speed), and supercritical flow (greater than critical speed). Critical flow represents a balance state where any increase in energy causes a transition to supercritical flow, while subcritical flow is characterized by lower velocities and depth. Understanding these classifications helps predict flow behavior, energy movement, and potential hazards, such as flooding.
Examples & Analogies
Imagine a racetrack with cars. If the cars are moving slowly (subcritical), they can easily navigate turns. At critical speed, they balance speed and control just right. But if they speed up too much (supercritical), they might risk losing control. Similarly, engineers need to understand these flow types to design safe and efficient waterways, just like ensuring cars are kept at the right speed for safety.
Velocity Profiles in Open Channel Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Anyway that is maybe a simple way to explaining you not going through this pressure is equal to the atmospheres and the pressure flow energy is not significant in this case that is the reasons maybe it is come that but let me not we have these the cover does not matter it okay.
Detailed Explanation
In open channel flows, one important aspect is understanding pressure conditions at the water's surface, which is usually atmospheric pressure. Unlike in pipes where pressure can build up, in open channels, the surface pressure is atmospheric, making it essential to focus on gravitational forces and drag from channel surfaces. This understanding is crucial when analyzing how quickly water flows and how it interacts with the channel bed and banks, as these factors significantly affect energy loss in flow.
Examples & Analogies
Think about a swimming pool. The water surface is exposed to the atmosphere, and we directly see its depth without worrying about pressure buildup inside because it has no covering. Just like a pool, understanding these pressure conditions in open channel flow helps civil engineers predict how water behaves as it moves, ensuring effective designs for channels, rivers, and drainage systems.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Open Channel Flow: Fluid flows in a channel open to the atmosphere with a free surface.
-
Velocity Distribution: The variation in fluid velocity, influenced by friction and gravitational forces.
-
Hydraulic Radius: A key factor in characterizing flow, defined as area of flow divided by the wetted perimeter.
-
No-slip Condition: Indicates fluid velocity is zero at channel boundaries.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a river bend, velocity is higher in the center and lower at the banks due to friction.
-
In rectangular canals, the hydraulic radius can be calculated to determine flow characteristics.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In channels wide and rivers deep, velocity dances, its secrets keep; from the surface high, it starts to dip, down to zero, at boundary's grip.
📖 Fascinating Stories
-
Imagine a river flowing through a forest. As the flow moves closer to the banks, it slows down and allows leaves to rest on the surface while the center rushes forward with maximum speed.
🧠 Other Memory Gems
-
Friction Forces Fastest Fluid: Remember that in open channels, friction slows down the velocity, making it fastest at the top surface.
🎯 Super Acronyms
VFC
- Velocity Fastest Center (indicating where the velocity is highest in open channels).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Open Channel Flow
Definition:
A type of fluid flow where the fluid flows in an open channel with a free surface exposed to the atmosphere.
-
Term: Velocity Distribution
Definition:
The variation of velocity across the section of flow in open channels, often depicted with velocity contours.
-
Term: NoSlip Boundary Condition
Definition:
The principle that fluid velocity equals zero at the boundary of an object it is in contact with.
-
Term: Hydraulic Radius
Definition:
The ratio of the cross-sectional area of flow to the wetted perimeter, used in open channel flow calculations.
-
Term: Free Surface
Definition:
The surface of a fluid that is in contact with the atmosphere; typically where pressure is atmospheric.