Examples of Inner Product Spaces
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Euclidean Space
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

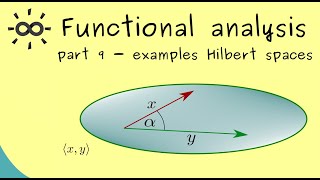
Today, we'll start with our first inner product space example, which is Euclidean space, R^n. Can anyone tell me how we define the inner product here?

Isn't it the dot product that we use?

Exactly! The inner product in this space is given by ⟨u,v⟩ = ∑(u_i * v_i). It's important for measuring lengths and angles, just like in geometry. Can anyone explain why this is useful?

We use it to find angles and distances between vectors, right?

Correct! Just remember the acronym 'DLA' for Dot product, Lengths, and Angles. This will help you remember the relevance of the inner product!

What if we have vectors in complex space instead?

Good question! We will get to that. But first, can you summarize today's main point?

The inner product in Euclidean space helps determine angles and lengths through the dot product!

Well done!
Understanding Complex Space
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s discuss the second example: complex space, C^n. Who remembers how we define an inner product here?

It’s similar to the Euclidean space but involves taking complex conjugates, right?

That’s right! The inner product is defined as ⟨u,v⟩ = ∑(u_i * \overline{v_i}). Why do you think we need the complex conjugate?

It ensures the product is a real number, right?

Exactly! And that’s crucial for the positive definiteness property of our inner product space. 'RCP' is a helpful mnemonic: Real numbers, Complex conjugates, and Positive definiteness.

Can this also represent angles?

Yes! It enables us to explore angles between complex vectors as well. Let’s summarize what we learned: the inner product across complex spaces ensures the necessary properties for analyzing various phenomena.

So both inner products help us measure angles and lengths!

Precisely!
Function Space Inner Product
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s turn to the third example which involves function spaces, C[a,b]. How do we define the inner product here?

It's defined using an integral, right?

Correct! The inner product is given by ⟨f,g⟩ = ∫ from a to b of f(x)g(x) dx. Why is this important?

We can use this in engineering applications, like approximation techniques?

Exactly, well done! The integral helps us collide with the functions over an interval, providing geometric interpretations in higher dimensions. Keep that in mind—let's use the acronym 'INT' for Integrals, Numerical applications, and Techniques.

What’s an example of its application?

It’s crucial in Fourier series and in solving differential equations! Can anyone summarize today's exploration?

The inner product in function spaces is defined by integration, and it’s useful in engineering!

Great job!
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section describes several prominent examples of inner product spaces. It elaborates on Euclidean space with the standard dot product, complex space defined similarly but with complex numbers, and function spaces that utilize integration to establish inner products. These examples serve as foundational applications within both mathematical theory and civil engineering practices.
Detailed
Examples of Inner Product Spaces
This section explores various examples of inner product spaces, emphasizing their definitions and applications in both theoretical and practical contexts. The inner product extends the notion of geometric relationships in higher dimensions, enriching the analysis across countless disciplines, particularly in engineering.
1. Euclidean Space Rn
The example of Euclidean space
- Defined as vectors, for instance,
- u = (u1, u2, ..., un) and v = (v1, v2, ..., vn).
-
The inner product, known as the dot product, is defined as:
$$ \langle u, v \rangle = \sum_{i=1}^{n} u_i v_i $$
- This expression forms a foundational building block for evaluating lengths and angles in geometry.
2. Complex Space Cn
- Similar to Euclidean space but accommodates complex numbers:
- The inner product becomes:
$$ \langle u, v \rangle = \sum_{i=1}^{n} u_i \overline{v_i} $$
where \overline{v_i} denotes the complex conjugate of v_i.
3. Function Space
- The space of continuous real-valued functions over an interval, denoted as C[a, b]:
-
The inner product is defined via integration as:
$$ \langle f, g \rangle = \int_a^b f(x)g(x) \, dx $$
- Demonstrating significant applications in engineering, particularly in solving differential equations and approximation problems.
These examples collectively illustrate how inner product spaces arise across various mathematical contexts, offering essential tools for geometric and analytical applications in fields, including civil engineering.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Euclidean Space Rn
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let u=(u₁,u₂,...,uₙ) and v =(v₁,v₂,...,vₙ), then:
⟨u,v⟩= ∑ (uᵢ * vᵢ)
i=1
This is the standard dot product.
Detailed Explanation
In Euclidean space Rⁿ, an inner product is computed using the sum of the products of corresponding entries of two vectors. For example, if u and v are two vectors in a 3-dimensional space, u = (u₁, u₂, u₃) and v = (v₁, v₂, v₃), then their inner product ⟨u, v⟩ is calculated as u₁ * v₁ + u₂ * v₂ + u₃ * v₃. This operation gives a scalar value that helps determine the angle between the two vectors and their lengths.
Examples & Analogies
Think of two vectors as arrows pointing in space. The inner product is like measuring how aligned these arrows are. If the arrows point in the same direction, the inner product is large; if they are at right angles, the inner product is zero, indicating no alignment.
Complex Space Cn
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let u,v ∈Cⁿ, then:
⟨u,v⟩= ∑ (uᵢ * vᵢ)
i=1
Detailed Explanation
In complex spaces, the inner product of two complex vectors also involves a summation of the products of their components. Here, if u = (u₁, u₂, …, uₙ) and v = (v₁, v₂, …, vₙ) are complex vectors, the inner product is computed as ⟨u, v⟩ = u₁ * v₁ + u₂ * v₂ + ... + uₙ * vₙ, with the important distinction that for complex inner products, each component's value might need to be conjugated for proper evaluation.
Examples & Analogies
Imagine two waves in water that can have different heights and complex energy contributions. Their interaction can be assessed by taking their inner product, similar to how we analyze how much they reinforce or cancel each other.
Function Space
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let V be the space of real-valued continuous functions on the interval [a,b], i.e., V = C[a,b]. The inner product is defined as:
⟨f,g⟩= ∫[a,b] f(x)g(x)dx
Detailed Explanation
In spaces of functions, like C[a,b], the inner product is defined as an integral of the product of two functions over a specified interval. For two functions f(x) and g(x), the inner product ⟨f, g⟩ calculates how similar the shapes of these functions are when plotted on a graph. More specifically, it captures the area under the curve formed by multiplying the two functions across the interval from a to b.
Examples & Analogies
Consider two shapes made by different materials that can be represented as functions—we can measure how much heat energy they can absorb together by intertwining them. The inner product gives us a quantitative measure of their interaction over a defined range.
Key Concepts
-
Inner Product: A function mapping vectors to real numbers that captures geometric relationships.
-
Euclidean Space: Defined using real numbers and the dot product, fundamental in geometry.
-
Complex Space: Similar to Euclidean but includes complex numbers and conjugate symmetry in the inner product.
-
Function Space: An integral-based inner product defined for continuous functions over an interval.
Examples & Applications
For Euclidean space R^2, the inner product of vectors (1,2) and (3,4) is calculated as ⟨(1,2),(3,4)⟩ = 13 + 24 = 11.
In function space C[0,1], the inner product of functions f(x)=x and g(x)=x^2 is ⟨f,g⟩ = ∫(0 to 1) x*x^2 dx = ∫(0 to 1) x^3 dx = 1/4.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In R, the dot does start, angles and lengths play a part.
Stories
Imagine two vectors, u and v, meeting at a point. Their dot product reveals the angle they make, like a clock striking noon.
Memory Tools
Remember 'I for Integration' to recall that in function space, the inner product is about integrating functions.
Acronyms
Use the acronym 'EDUF' for Euclidean, Dot product, Understanding Complex, Function space.
Flash Cards
Glossary
- Inner Product
A function that defines a geometric relationship between two vectors in a space, satisfying linearity, symmetry, and positive definiteness.
- Euclidean Space
A finite-dimensional space defined with real numbers equipped with the standard inner product (dot product).
- Complex Space
A vector space with complex numbers that uses a conjugate symmetry in its inner product definition.
- Function Space
Space of functions where the inner product is defined through integration over an interval.
- Dot Product
The inner product for vectors in Euclidean space, summing the products of corresponding components.
Reference links
Supplementary resources to enhance your learning experience.
