Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Vector Projection
Unlock Audio Lesson
Today, we will discuss the projection of vectors. Can anyone tell me what they understand by projecting a vector onto another?
Isn't it like casting a shadow of one vector onto another?
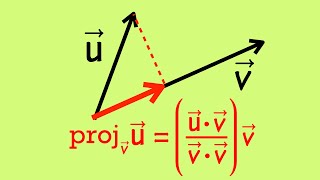
Exactly! The projection of vector **u** onto vector **v** is mathematically represented as proj_v(u). It’s defined by the formula: proj_v(u) = (⟨u, v⟩ / ⟨v, v⟩) v. This highlights how we can express **u** in the direction of **v**.
Can you explain what each part of that formula means?
Certainly! ⟨u, v⟩ is the dot product, giving us the component of **u** in the direction of **v**, and ⟨v, v⟩ normalizes this projection.
What’s the significance of this in real-life applications?
Great question! This concept is vital in fields like structural engineering, where projections help in modeling structures accurately.
To remember the formula, think of the acronym PUV: Projection of u onto v using ⟨u, v⟩ over ⟨v, v⟩.
In summary, projecting vectors allows us to break down complex vector relationships into manageable components.
Applications in Engineering
Unlock Audio Lesson
Let’s look at some applications. Why do you think projection is essential in civil engineering?
Maybe for calculating forces in structures?
Correct! Engineers project forces onto structural elements to assess stress and optimize designs. Can anyone think of another area where this might be applicable?
How about in least squares approximation?
Exactly! In least squares, we seek the best-fit line, which involves projecting data points onto a vector representing that line. This minimizes errors effectively.
Do we always need to know precise angles?
Not necessarily! The projection formula allows for calculations without direct measurement of angles, which simplifies many engineering challenges.
To remember the application: think of vectors as 'directional buddies' guiding you in finding optimal solutions across various engineering fields.
In summary, understanding vector projections helps us model, analyze, and optimize many engineering phenomena.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concept of vector projection is introduced, detailing how to project vector u onto vector v using the inner product properties. This principle is crucial for applications in least squares approximation and structural modeling.
Detailed
Projection of Vectors
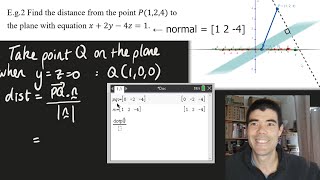
The projection of a vector u onto another vector v is a fundamental concept within inner product spaces, defined mathematically as:
$$\text{proj}_{v}(u) = \frac{\langle u,v \rangle}{\langle v,v \rangle} v$$
This projection provides a way to express vector u in terms of vector v, which is essential in many mathematical and engineering applications. The projection helps visualize the concept of approximating a vector in the direction of another and is particularly relevant in engineering fields, like civil engineering, for modeling structures and optimizing designs through least squares methods. Furthermore, this mathematical foundation is pivotal for understanding orthogonal decompositions, where vectors can be analyzed based on their individual contributions to a subspace.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Vector Projection
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The projection of a vector u onto another vector v is defined as:
$$
\text{proj}_v u = \frac{\langle u, v \rangle}{\langle v, v \rangle} v
$$
Detailed Explanation
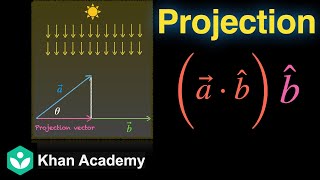
This formula defines how to project a vector u onto another vector v. Projection involves finding a vector that represents u in the direction of v. The formula uses the inner product, \langle u, v \rangle, which measures how much of u is in the direction of v. It also involves dividing by \langle v, v \rangle to ensure that the projection is scaled correctly, thus giving the 'shadow' or implied direction of u along v.
Examples & Analogies
Think of casting a shadow on the ground. If the sun is shining directly overhead (the vector u), the shadow on the ground (the projection onto the vector v) shows how much of the original object lies in the same direction as the ground. Just like how shadows change length and direction with the position of the sun, the projection of a vector changes based on the direction and length of the vector it is projected onto.
Applications of Vector Projection
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This concept is foundational in least squares approximation, structural modeling, and orthogonal decompositions.
Detailed Explanation
Vector projections are used in various applications. One key application is the least squares approximation, where we want to find the closest point on a vector space to a given point. By projecting onto a subspace, we can determine the best fit, which minimizes the error between observed and predicted values in data science. In structural modeling, projections help to analyze forces and moments acting in different directions on a structure, ensuring stability and safety.
Examples & Analogies
Imagine you're trying to fit a line through a set of points on a graph. The line represents an ideal outcome based on your data. The projection of each point onto the line shows how far off each point is from the line, indicating the best fit. This is akin to finding the optimal path when navigating through a city — the projection tells you how to stay on the best route while minimizing detours.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Projection: The projection of vector u onto vector v can be calculated using the formula proj_v(u) = (⟨u, v⟩ / ⟨v, v⟩) v.
-
Inner Product: The inner product serves as a foundational operation in defining the projection mathematically and geometrically.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Project the vector u = (3, 4) onto vector v = (1, 1). Using the projection formula, we find proj_v(u).
-
Example 2: In a structural analysis scenario, projecting forces acting on a beam can help determine stress distributions along its length.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To project a vector, it’s easy to see, we multiply the dot product by the vector’s decree.
📖 Fascinating Stories
-
Imagine a tall building casting a shadow on the ground in the direction of the sun. The shadow represents the projection of the building onto the ground.
🧠 Other Memory Gems
-
Use the acronym PUV: Projection of u onto v using ⟨u, v⟩ over ⟨v, v⟩.
🎯 Super Acronyms
PUV helps remember how to project
- P: for Project
- U: for u and V for vector v.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Projection
Definition:
The representation of a vector in the direction of another vector.
-
Term: Inner Product
Definition:
A mathematical operation that allows the measurement of angles and lengths in vector spaces.
-
Term: Least Squares Approximation
Definition:
A statistical method used to minimize the differences between observed and predicted values.
-
Term: Orthogonal Decomposition
Definition:
A technique for expressing vectors based on their components with respect to an orthogonal basis.