Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Norms
Unlock Audio Lesson
Today, we're going to discuss the concept of a norm induced by the inner product. Can anyone tell me what a norm represents in mathematical terms?
Isn't it a measure of the length or size of a vector?
Correct! The norm gives us the length of a vector. In an inner product space, we use the inner product to define this length. The formula is given by the square root of the inner product of that vector with itself, written as ∥v∥ = sqrt(⟨v,v⟩).
So, using that formula, we can measure how far apart two vectors are from each other, right?
Exactly! The norm helps us define the distance between vectors, which is crucial in understanding concepts like angles and orthogonality.
Application of Norm in Inner Product Spaces
Unlock Audio Lesson
Now, let's explore some applications of norms in inner product spaces. Why do you think understanding distance and angles is important in higher dimensions?
It helps in visualizing relationships between vectors in multidimensional settings!
That's right! When we understand distances and angles, we can apply this knowledge to solve real-world problems, such as in engineering or physics.
Can you give an example of how it's applied in engineering?
Absolutely! In structural engineering, we need to ensure that loads applied to structures are balanced. The norms can help us determine whether the forces are aligned or need adjustment.
Key Properties of Norms
Unlock Audio Lesson
Let's discuss some key properties of norms. What do you think a norm must satisfy?
I believe the norm needs to be non-negative?
That's a crucial property! Additionally, the norm must equal zero if and only if the vector is the zero vector. These properties are foundational in understanding how norms behave.
And we can scale vectors too, right? If we multiply a vector by a scalar, how does that affect the norm?
Good question! The norm should also satisfy ∥αv∥ = |α| ∥v∥, where α is a scalar. This means scaling will affect the length proportionally.
So, if we make a vector twice as long, its norm should also double!
Exactly! Great understanding of norms.
Conclusion and Recap
Unlock Audio Lesson
To wrap up today’s session, can anyone summarize what we learned about norms in inner product spaces?
We learned that norms measure the length of vectors, are defined using the inner product, and are important for defining distances and angles!
Well done! Remember that these concepts are foundational not just in mathematics but also in various applications in engineering and physics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we learn that the norm of a vector in an inner product space is determined using the formula derived from the inner product. This approach helps in measuring distances and angles between vectors in various mathematical applications.
Detailed
Norm Induced by Inner Product
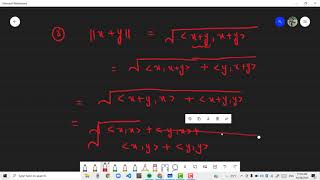
In an inner product space, the norm (or length) of a vector v is given by the square root of the inner product of the vector with itself, represented mathematically as v = ⟨v, v⟩^{1/2}.
This norm provides a way to calculate the distance between two vectors, allowing us to define concepts of angle and orthogonality in higher dimensional spaces. Therefore, understanding this norm is fundamental in various applications, particularly within fields that utilize linear algebra, geometry, and mathematical modeling.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Norm
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In an inner product space, the norm or length of a vector v is given by:
∥v ∥= ⟨v,v⟩
Detailed Explanation
A norm is a function that assigns a non-negative length or size to a vector. In an inner product space, the norm of a vector v can be computed using the inner product of the vector with itself. The formula ∥v ∥ = ⟨v, v⟩ means that you take the inner product of the vector with itself, which effectively measures its length. The result of this operation is always non-negative.
Examples & Analogies
Imagine the norm of a vector as a measure of how long a rope is. If you take a rope and stretch it out straight, you can measure its length. Similarly, the norm gives you the 'length' of a vector in the abstract space defined by the inner product.
Significance of Norm
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This norm allows us to define distance and angle between vectors.
Detailed Explanation
The norm is a crucial concept because it provides a way to quantify the 'size' of a vector. Once we have a way to measure size, we can also use it to measure the distance between two vectors. The distance can be calculated using the norms of the vectors involved. Further, the norm helps define the angle between vectors using the inner product, which is fundamental in understanding geometric relationships in higher-dimensional spaces.
Examples & Analogies
Think of the norm as a ruler and the vectors as arrows pointing in different directions. Just like you can measure the straight-line distance between two points (the tips of two arrows) using a ruler, you can use the norm to measure the distance between two vectors and understand how closely they point in the same direction.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Norm: Measures the length of a vector in an inner product space, defined as ∥v∥ = sqrt(⟨v,v⟩).
-
Inner Product: A crucial operation in vector spaces that helps derive concepts like norms and orthogonality.
-
Distance: The length between two vectors measured using their norms.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For vector v = (3, 4) in R², the norm is calculated as ∥v∥ = sqrt(3² + 4²) = 5.
-
In function spaces, if f(x) is continuous on [0, 1] with sup norm, the norm can be represented as ∥f(x)∥ = max |f(x)| for x in [0, 1].
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Norm is the length that we adore, the square root of the inner product’s core.
📖 Fascinating Stories
-
Imagine two friends, Norm and Inner, who measure their heights by using the inner product of their numbers to find the true length of their friendship.
🧠 Other Memory Gems
-
L.A.S. for Norm: Length, Angle, Size.
🎯 Super Acronyms
N.I.C.E. - Norm Induced by the Inner-product for calculating length easily.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Norm
Definition:
A function that assigns a length or size to vectors in an inner product space.
-
Term: Inner Product
Definition:
A mathematical operation that combines two vectors to produce a scalar, satisfying specific properties.
-
Term: Vector
Definition:
An element of a vector space, represented as an ordered tuple of numbers.