Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Inner Products
Unlock Audio Lesson
Today, we're exploring the inner product in complex vector spaces, which is crucial for various engineering applications. Can anyone tell me what an inner product entails?
Is it similar to the dot product in real spaces?
Exactly! The inner product in complex spaces is a generalization of the dot product but involves complex components. It's defined as $$⟨u,v⟩ = \sum_{i=1}^{n} u_i \overline{v_i}$$, where $\overline{v_i}$ is the complex conjugate of the components of vector v.
What ensures that this operation is well-defined?
Good question! The use of the complex conjugate ensures that properties such as positive definiteness are satisfied, which is fundamental to inner product spaces.
Example Calculation
Unlock Audio Lesson
Let's compute an inner product together. Consider the vectors u = (1+i, 2-i) and v = (i, 3+2i). What would the first step be?
We should find the complex conjugate of v first, right?
Correct! The complex conjugate of v = (i, 3+2i) is (−i, 3−2i). Next, can someone compute the products of corresponding components?
That gives us: (1+i)(−i) + (2−i)(3−2i).
Exactly! Now, let’s calculate that step-by-step for clarity.
Applications of Inner Products
Unlock Audio Lesson
Now that we understand inner products, why do you think this concept is important in engineering?
It seems like it could be used in vibration analysis or similar fields.
Exactly! Inner products are key in vibration analysis, electromagnetic theory, and modeling complex structures. They help us ensure stability and predict behavior under various conditions.
Can we also use them in structural modeling?
Yes, they’re essential in complex structural modeling as they allow for the analysis of forces in structures and help in optimizing designs.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The inner product in complex vector spaces generalizes the idea of the dot product used in real spaces, incorporating complex conjugates to ensure positive definiteness. Understanding this concept is vital in applications, such as vibration analysis and complex structural modeling.
Detailed
In complex vector spaces, specifically denoted as V = C^n, the inner product is defined by the formula:
$$⟨u,v⟩ = \sum_{i=1}^{n} u_i \overline{v_i}$$
This formula uses the complex conjugate of the second vector, ensuring properties like positive definiteness hold true. An example involves vectors u = (1+i, 2-i) and v = (i, 3+2i), where the inner product is computed through summation of the products of the respective components, adjusted for the complex conjugate. This framework is extensively applied in fields like vibration analysis, electromagnetic theory, and complex structural modeling, showcasing the importance of understanding inner products in various complex dimension settings.
Youtube Videos
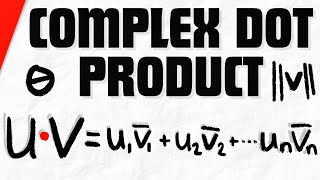
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Example of Inner Product Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example:
Let u=(1+i,2−i), v =(i,3+2i)
$$\langle u,v \rangle=(1+i)i+(2−i)(3+2i)=(1+i)(-i)+(2−i)(3-2i)$$
Compute each term to get the inner product.
Detailed Explanation
This example illustrates how to compute the inner product for two specific complex vectors. Here, you need to multiply each element of vector 'u' with the conjugate of the corresponding element in vector 'v'. The first term involves multiplying 1+i with i, and the second term involves multiplying 2−i with the conjugate of 3+2i. After performing the multiplication, you would provide the sum of these products to find the inner product. Note how each step involves careful handling of complex numbers.
Examples & Analogies
Imagine you are blending two different flavors, like chocolate and vanilla, to create a dessert. Just as you would need to consider each flavor's properties (sweetness, texture) to understand how they interact and contribute to the final taste, calculating the inner product requires careful consideration of how each component of the complex vectors contributes to the overall result.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Inner Product in Complex Spaces: It is defined with the complex conjugate to ensure properties like positive definiteness.
-
Complex Conjugate: The complex conjugate of a complex number is necessary for calculating inner products in complex vector spaces.
-
Applications: Used in vibration analysis, electromagnetic theory, and structural modeling.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example: Let u = (1+i, 2-i) and v = (i, 3+2i). The inner product is calculated as $$⟨u,v⟩=(1+i)(-i)+(2-i)(3-2i)$$, demonstrating how complex conjugates influence the result.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In complex space, we take special care, conjugates help our inner product fare.
📖 Fascinating Stories
-
Imagine a bridge swaying gently; engineers use inner products to study its vibrations, ensuring it stands strong.
🧠 Other Memory Gems
-
Remember the acronym CONC: Conjugate Use, Order Matters, Needing Complex.
🎯 Super Acronyms
I-PROMISE
- Inner-Product in Real and OPtimized Modeling In Various Engineering.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Inner Product
Definition:
A mathematical operation defined on a vector space, which allows measuring angles and lengths, and involves the complex conjugate in complex spaces.
-
Term: Complex Conjugate
Definition:
For a complex number a + bi, the complex conjugate is a - bi.
-
Term: Vibration Analysis
Definition:
A field of engineering that studies the oscillations of physical systems.