Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Triangle Inequality
Unlock Audio Lesson
Today, we are going to learn about the Triangle Inequality. Can anyone tell me what that means in a geometrical sense?
Is it about the lengths of the sides of a triangle?
Exactly! The Triangle Inequality helps us understand that the length of one side of a triangle is less than or equal to the sum of the other two sides. In terms of vectors, we say that for any vectors u and v, the norm of their sum is less than or equal to the sum of their norms.
So it’s like saying that the direct distance between two points is shorter than walking along two sides?
Great analogy! Yes, it shows that taking a straight path is always the shortest.
Mathematical Representation of Triangle Inequality
Unlock Audio Lesson
Now, let’s look at the mathematical form of the Triangle Inequality: ||u + v|| ≤ ||u|| + ||v||. What does the notation ||.|| represent?
That’s the norm of a vector, right?
Correct! The norm indicates the length of the vector. The Triangle Inequality helps us understand how the lengths of vectors relate when we add them together.
Can you give us an example?
Of course! If u = (3, 4) and v = (1, 2), calculating gives us ||u + v|| = ||(3+1, 4+2)|| = ||(4, 6)||. Can anyone compute that?
It’s 7.21, if I use the Pythagorean theorem!
Exactly! And remember, ||u|| + ||v|| also computes to 5 + 2. So the Triangle Inequality holds here.
Application of Triangle Inequality
Unlock Audio Lesson
Now let’s discuss why the Triangle Inequality is important there are many applications in engineering. Can anyone think of how this might help in stability analysis?
Maybe it helps us predict how structures behave under loads?
Yes, absolutely! It provides bounds on how forces and displacements interact. You can also use it to ensure convergence in numerical methods.
That makes sense; it means we can be sure our solutions don’t explode, right?
Exactly, well put! The Triangle Inequality ensures that the distances and angles we work with lead to stable solutions in our models.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Triangle Inequality is a fundamental principle in inner product spaces expressing that the norm of the sum of two vectors is less than or equal to the sum of their norms. This theorem underlines many concepts in mathematics and fields like engineering, offering crucial implications in areas such as convergence and stability.
Detailed
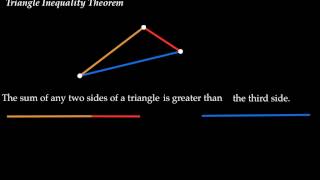
Triangle Inequality
The Triangle Inequality states that for any vectors u and v in an inner product space, the following relationship holds:
$$
\|u + v\| ≤ \|u\| + \|v\|
$$
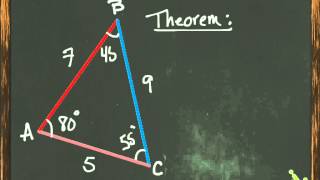
This concept arises from the geometric interpretation of vector addition, indicating that the straight-line distance (the length of the vector u + v) between two points (represented by vectors u and v) is always less than or equal to the sum of the distances to each point from the origin. In essence, it captures the idea that forming a triangle with two sides (the vectors) cannot longer than the length of the side directly connecting the endpoints.
Significance
The Triangle Inequality has important implications in mathematical analysis, particularly in ensuring convergence in iterative methods and proving stability. It serves as a foundational principle in various applications in Civil Engineering, especially when dealing with approximations and solutions to systems of equations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the Triangle Inequality
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
∥u+v ∥≤∥u∥+∥v ∥
Detailed Explanation
The triangle inequality states that the length (or norm) of the sum of two vectors (u and v) is less than or equal to the sum of their individual lengths. This property is essential in vector spaces and signifies that the direct path connecting two points (the sum of vectors u and v) cannot exceed the length of two individual paths from the origin to these points.
Examples & Analogies
Imagine you are standing at point A and need to travel to point B. You can either take a direct path straight to B, or you can walk to point C first and then from C to B. The triangle inequality suggests that walking directly from A to B will always be shorter or equal to the distance if you choose to stop at point C.
Implications of the Triangle Inequality
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is a direct consequence of the inner product structure and has important implications in convergence, stability, and bounding solutions.
Detailed Explanation
The triangle inequality not only defines a fundamental rule for distance in vector spaces but also plays a critical role in mathematical analysis and applied fields, such as engineering. It ensures that sequences converge correctly in inner product spaces, facilitates stability in numerical methods, and helps to bound solutions, making it an essential foundation for problem-solving in various scenarios.
Examples & Analogies
Consider a tightrope walker trying to maintain balance. The triangle inequality represents the principle that the walker's net movement (the sum of small steps to the left and right) should not exceed their original balance capability. If the net movement becomes too great, it could lead to a fall, analogous to how violation of the triangle inequality can lead to mathematical inconsistencies.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Triangle Inequality: Explains the relationship between the lengths of vectors and their sums.
-
Norm: A measure of the length of a vector within an inner product space.
-
Boundedness: The concept that limits the behavior of functions or vectors in vector spaces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For vectors u = (3, 4) and v = (1, 2), calculating the norms: ||u + v|| = ||(4, 6)|| = 7.21, and ||u|| + ||v|| = 5 + 2 = 7. The Triangle Inequality holds: 7.21 ≤ 7.
-
If u = (1, 1) and v = (-2, -2), ||u + v|| = ||(-1, -1)|| = √2 which is less than ||u|| + ||v|| = 2 + √8.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When adding up two sides with glee, the longest path's a straight spree!
📖 Fascinating Stories
-
Imagine two friends walking from home to a cafe. They could either walk straight or take a longer route. The shortest, quickest route always gets them there fastest!
🧠 Other Memory Gems
-
Remember: STAY = Sum Two adjacent sides Always less than the third side!
🎯 Super Acronyms
TIS = Triangle Inequality Satisfied. Use this acronym to remember the principle.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Triangle Inequality
Definition:
A fundamental principle stating that in an inner product space, the length of the sum of two vectors is less than or equal to the sum of their lengths.
-
Term: Norm
Definition:
A function that assigns a non-negative length or size to vectors in an inner product space.
-
Term: Inner Product Space
Definition:
A vector space equipped with an inner product, allowing for angles and lengths to be measured.