Orthogonal Complement
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Orthogonal Complement
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're diving into the concept of the orthogonal complement. Can anyone tell me what a subspace is?

A subspace is a subset of a vector space that is also a vector space itself.

Exactly! Now, if W is a subspace of V, what do you think W⊥ represents?

It's the set of all vectors in V that are orthogonal to every vector in W, right?

That's correct! Remember, we denote the orthogonal complement as W⊥. Let’s relate this to applications. Why do you think this is important in engineering?

Because we need to analyze forces and constraints in structures!

Great connection! Understanding these relationships helps engineers model and solve critical problems. Now, can someone summarize what we've discussed?

W⊥ is the set of vectors orthogonal to all vectors in W, which is important for decompositions in engineering applications.
Properties and Significance of W⊥
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we understand what W⊥ is, let’s explore its properties. Can anyone mention a key property of orthogonal complements?

I think there’s a relationship about direct sums, like W + W⊥ = V if W is closed.

Exactly! This means that every vector in V can be uniquely represented as the sum of a vector from W and one from W⊥. How does this help in real-world applications?

It allows us to simplify complex problems by isolating components related to specific directions in space.

Spot on! This isolation is crucial for analysis in structural engineering. Let's move to our next point: can someone remind us about the inner product relationship?

It's the inner product that defines the orthogonality condition, right? So if two vectors have a zero inner product, they are orthogonal.

Right! So understanding W⊥ requires us to understand how the inner product works.

Correct! The inner product is a foundational concept here. To summarize, W⊥ allows us to decompose the space, simplifying problems in engineering design.
Applications of Orthogonal Complements
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s talk about specific applications of the orthogonal complement in civil engineering. Can anyone give me an example?

In modal analysis, we deal with structures vibrating. The modes themselves are often analyzed using orthogonal complements.

That’s a great example! Modal analysis benefits greatly from understanding orthogonality. What about boundary conditions?

We can use orthogonal complements to derive conditions that isolate certain behaviors of a structural element.

Excellent point! Proper boundary conditions are crucial for realistic modeling. Remember, every time we decompose a problem, we leverage these concepts of orthogonality. Can anyone summarize today's learning?

We learned that the orthogonal complement W⊥ helps in decomposing vector spaces which is vital in applications like modal analysis and boundary conditions in civil engineering.

Perfect summary! Understanding these concepts will enhance your problem-solving toolkit as you move forward.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
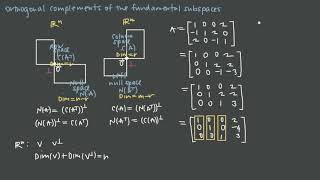
The orthogonal complement, denoted as W⊥, consists of all vectors in a vector space V that are orthogonal to every vector in a subspace W. This concept is crucial for decomposing vector spaces into direct sums and is particularly important in engineering applications such as boundary conditions and modal analysis.
Detailed
Orthogonal Complement
In this section, we examine the notion of the orthogonal complement in inner product spaces. Let W ⊆ V be a subspace of an inner product space V. The orthogonal complement W⊥ is defined as the set of all vectors in V that satisfy the condition ⟨v,w⟩ = 0 for every w in W. This key idea allows us to decompose spaces into direct sums, where V can be expressed as a sum of W and its orthogonal complement.
The significance of this concept extends to various applications in civil engineering, especially in the analysis of boundary conditions and modal analysis, where understanding relationships among vectors plays a vital role in modeling complex systems.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Orthogonal Complement
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Given a subspace W ⊆V, the orthogonal complement W⊥ is the set:
W⊥ ={v ∈V |⟨v,w⟩=0 for all w ∈W}
Detailed Explanation
The orthogonal complement, denoted as W⊥, refers to all the vectors v in the larger vector space V that are orthogonal to every vector w in a given subspace W. This means that for each vector v in W⊥, if we take any vector w from W, the inner product ⟨v, w⟩ equals zero. The orthogonal complement is a way of identifying vectors that do not 'interact' with the vectors in W, thereby allowing us to understand the structure of the vector space more clearly.
Examples & Analogies
Consider a basketball court (the vector space V) with players (the vectors) on one half of the court (the subspace W). The area on the opposite half of the court where no player is standing can be thought of as the orthogonal complement W⊥. No player on one half is directly interacting with the players on the other half, just like how the vectors in W⊥ do not interact (through the inner product) with the vectors in W.
Importance of Orthogonal Complement
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This helps in decomposing spaces into direct sums and is important in the study of boundary conditions and modal analysis in Civil Engineering.
Detailed Explanation
Understanding the orthogonal complement is crucial when we want to break down a vector space V into simpler, mutually exclusive parts. When we can express V as a direct sum of W and its orthogonal complement W⊥, it simplifies many calculations, such as projecting vectors or solving systems of equations. In Civil Engineering, this concept is vital for analyzing structures by separating modes of vibration or different load scenarios into manageable components.
Examples & Analogies
Imagine a construction project where you need to analyze the forces on a bridge. You can think of the forces acting on the bridge as the subspace W and the resulting reactions or adjustments at the supports as W⊥. By understanding both parts, engineers can ensure that the bridge remains stable and safe, using the orthogonal complement to handle calculations that don’t overlap with the direct forces acting on the structure.
Key Concepts
-
Orthogonal Complement: The set of vectors orthogonal to every vector in a subspace W.
-
Decomposition of Vector Spaces: W and W⊥ can combine to form the whole space V, enhancing problem-solving.
-
Importance in Engineering: Vital for analyzing structures and solving complex problems.
Examples & Applications
If W is the span of vectors {(1, 0), (0, 1)}, then W⊥ includes all vectors of the form (a, b) where a and b are such that a ± b = 0.
In structural analysis, if W represents deflection modes of a beam, W⊥ characterizes additional modes independent of these deflections.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Vectors that are orthogonal, in W⊥ they reside,
Stories
Imagine a wise architect who builds bridges. In their plans, they identify W as the visible support structure and W⊥ as the unseen stability provided by the ground beneath.
Memory Tools
Remember W⊥ as 'W perpendicularly excluded,' focusing on components that do not influence each other.
Acronyms
WOP
is the Orthogonal Partner for finding W⊥.
Flash Cards
Glossary
- Orthogonal Complement
The set of all vectors in a vector space that are orthogonal to every vector in a given subspace.
- Subspace
A subset of a vector space that is also a vector space under the operations of vector addition and scalar multiplication.
- Inner Product
A mathematical operation that takes two vectors and returns a scalar, encapsulating geometric concepts such as angle and length.
- Direct Sum
A method of combining two or more subspaces such that every element of the larger space can be uniquely expressed as a sum of elements from the subspaces.
Reference links
Supplementary resources to enhance your learning experience.
