Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Independence
Unlock Audio Lesson
Today, we’re going to discuss linear independence in vector spaces. When we say a set of vectors is linearly independent, it means that the only way a linear combination of those vectors can equal zero is if all the coefficients are zero. Who can give me the mathematical representation of this idea?
Is it like saying a₁ * v₁ + a₂ * v₂ + ... + aₙ * vₙ = 0 implies that a₁ = a₂ = ... = aₙ = 0?
Exactly! That’s a perfect example. If any coefficient can be non-zero and still satisfy that equation, then the vectors are linearly dependent. Can anyone explain what it means for a set to be linearly dependent?
It means at least one vector can be expressed as a linear combination of the others, right?
Yes! Great job. Remember, linear independence is crucial when determining if a set of vectors can uniquely span a vector space.
Geometric Interpretation
Unlock Audio Lesson
Now let’s visualize linear independence. In R², how do we determine if two vectors are linearly independent?
They should not be collinear, meaning they don’t lie on the same line.
Exactly! And what about R³?
The vectors need to be non-coplanar to be independent. If they lie in the same plane, they are dependent.
Great understanding! Remember, geometric interpretations help solidify our understanding of linear independence.
Testing Linear Independence
Unlock Audio Lesson
We can also test for linear independence through algebraic methods. Who can outline the steps to verify if a set of vectors is independent?
We form a linear combination equal to the zero vector and set that up as a homogeneous system of equations.
Correct! And what do we look for in the solution of this system?
If the only solution is the trivial solution, they are independent; if we find non-trivial solutions, then they are dependent.
Yes! Very concise, everyone. Testing linear independence can often help us find a basis for the vector space.
Application in Engineering
Unlock Audio Lesson
Let’s discuss how linear independence applies in civil engineering. Why is it critical?
In structures, if the forces acting at joints are not independent, we can't ensure a unique solution to our force equations.
Exactly! And what about the finite element method?
They must have independent shape functions to represent solutions uniquely.
Great insights! Remember, understanding linear independence is vital in ensuring the structural integrity of engineering systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section elaborates on the concept of linear independence among vectors in a vector space, clarifying that a set is independent if the linear combination leading to the zero vector has only the trivial solution. It distinguishes linearly independent versus dependent sets and underscores geometric interpretations in R² and R³.
Detailed
Detailed Summary
In linear algebra, a set of vectors {v₁, v₂,..., vₙ} in a vector space V is declared to be linearly independent if the only solution to the equation;
a₁ * v₁ + a₂ * v₂ + ... + aₙ * vₙ = 0
is the trivial solution where all coefficients a₁, a₂, ..., aₙ are zero. If there exists any non-trivial solution (any aᵢ not equal to zero), the set is considered linearly dependent.
Key Idea
If at least one of the vectors can be represented as a linear combination of the others, this indicates linear dependence.
The significance of this concept is profound in various applications, including structural analysis in civil engineering, where assessing the independence of forces or vectors can define the stability of structures. The section provides foundational certifications and criteria for checking linear independence through algebraic approaches and establishes geometric representations in two-dimensional and three-dimensional spaces.
Youtube Videos
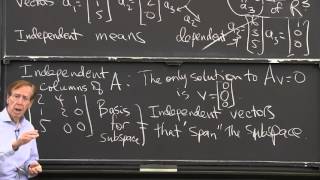
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Linear Independence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A set of vectors {⃗v 1,⃗v 2,...,⃗v n} in a vector space V is said to be linearly independent if:
a ⃗v +a ⃗v +⋯+a ⃗v =⃗0
1 1 2 2 n n
implies that
a 1=a 2=⋯=a n=0.
Otherwise, the set is called linearly dependent.
Detailed Explanation
The definition of linear independence states that a set of vectors is considered linearly independent if the only solution to their linear combination equaling the zero vector is when all the coefficients in that combination are zero. In other words, if you can create the zero vector using these vectors but the only way to do it is by making all of their coefficients zero, then they are independent. If you can find a solution where at least one of those coefficients is non-zero, then the vectors are dependent, meaning some of them can be expressed as combinations of the others.
Examples & Analogies
Imagine you have a group of friends. If each friend has a distinct skill, like one can cook, another can draw, and another can sing, they are like linearly independent vectors because you can't express any one friend's skill in terms of another's. However, if one friend is not just a good cook but can also draw really well, their skills overlap with another, making the group skill-dependent.
Key Idea of Linear Dependence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Key idea: If at least one vector in the set can be written as a linear combination of the others, the set is linearly dependent.
Detailed Explanation
This key idea highlights the condition of linear dependence. It states that if you can express one vector as a combination of the others in the set, then the vectors are dependent on each other. This means there is redundancy among the vectors because at least one is not adding new information or direction in the vector space.
Examples & Analogies
Think of a toolbox. If you have a wrench and a socket that can both turn bolts, having both tools may not add much value if they serve the same purpose. If you can turn a bolt using the wrench, bringing the socket may not be necessary—this is akin to having dependent vectors. You’ve got one tool doing the job of two, just like one vector does the work of another in a linearly dependent set.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Linear Independence: A concept defining a set of vectors as independent if the only solution to a specific linear combination is the trivial solution.
-
Linear Dependence: Occurs when at least one vector in a set can be expressed as a linear combination of the others.
-
Vector Space: A set of vectors with defined operations that retain closure and properties under addition and scalar multiplication.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Consider vectors [1, 2] and [3, 4]. They are linearly independent as there are no coefficients other than zero that satisfy a₁[1, 2] + a₂[3, 4] = [0, 0].
-
Example 2: The vectors [1, 2] and [2, 4] are linearly dependent because [2, 4] is just 2*[1, 2].
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Linear independence is a clear sight, zero's the answer, not a mix of light.
📖 Fascinating Stories
-
Imagine a group of friends trying to plan an event. If each friend has a unique role, that's like a linearly independent set; they can’t do each other's tasks. But if one can simply do what another does, they’re dependent—like repeating jobs in a big team!
🧠 Other Memory Gems
-
Use 'I' for Independent and 'Z' for Zero: If the coefficients all equal zero, they are Independent!
🎯 Super Acronyms
Remember the acronym 'SPADES'
- S: for Set
- P: for Polynomial
- A: for A-coefficient
- D: for Dependence
- E: for Equations
- S: for Solutions to recall the aspects of linear independence.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear Independence
Definition:
A set of vectors is linearly independent if the only solution to their linear combination equalling zero is the trivial solution where all coefficients are zero.
-
Term: Linearly Dependent
Definition:
A set of vectors is linearly dependent if at least one vector can be expressed as a linear combination of the others.
-
Term: Vector Space
Definition:
A mathematical structure formed by a collection of vectors, where vector addition and scalar multiplication are defined.
-
Term: Linear Combination
Definition:
A sum of scalar multiples of vectors, forming a new vector in the vector space.