Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Independence
Unlock Audio Lesson
Today, we'll explore the concept of linear independence. Can anyone tell me why this concept is essential in vector spaces?
It helps determine if vectors are redundant!
Exactly! Linear independence tells us if a set of vectors can uniquely represent a subspace. Let's dive deeper into what we mean by a linear combination of vectors.
Is that when you add vectors together with scalars?
Precisely! A linear combination is formed by taking scalars and summing their respective vectors. If the only way to produce the zero vector is with all scalars equal to zero, we have a linearly independent set. Remember, this leads to the definition!
So, if there's another way to get to zero, they are dependent?
Yes, great summary! Let’s remember this distinction: independence = unique representation. Does anyone have questions on this?
Geometric Interpretation
Unlock Audio Lesson
Let's translate our concepts into geometry. In R^2, when do we consider two vectors to be linearly independent?
If they are not collinear?
Correct! If two vectors span a plane, they must not align. What about in R^3?
Ah, they should not be coplanar!
Yes!! They must span the entire 3D space. Visual aids can help us remember this: two vectors in a plane and three non-coplanar vectors in space. That's crucial!
I see how this connects to structural analysis!
Absolutely, geometric interpretations are foundational in engineering! We need to understand dependencies for structure stability.
Algebraic Criteria for Testing Independence
Unlock Audio Lesson
Now let's discuss how to test if a set of vectors is linearly independent using algebra. What steps do we take first?
We form the linear equation equal to the zero vector?
Exactly! Next, how do we transform that?
Into a homogeneous system of equations?
Right! After that, we solve it. What indicates independence?
Only the trivial solution indicates independence!
Great! So, it’s essential to practice this method. Let’s do an example together after this session!
Applications in Engineering
Unlock Audio Lesson
To wrap up, let’s discuss how linear independence applies to civil engineering. Can anyone provide an example?
In structural analysis, the forces need to be independent!
Correct! Independent forces lead to unique solutions for structures. What about in the finite element method?
The shape functions need to be independent to represent solutions!
Right again! It’s essential for stability in our designs. Remembering to check for dependencies can prevent errors in analysis.
This all ties back to ensuring our structures are safe!
Exactly! Linear independence underpins the reliability of civil engineering solutions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explores the definition of linear independence within vector spaces, providing geometric and algebraic interpretations, criteria for testing independence, and applications in civil engineering contexts.
Detailed
Detailed Summary of Linear Independence
Linear independence is essential to the structure of vector spaces, specifically in systems of linear equations. A set of vectors is considered linearly independent if the only trivial solution to their linear combination resulting in the zero vector is when all coefficients are zero. The section provides a recap of vector spaces and bases, emphasizing that a basis comprises a linearly independent set that spans the vector space completely.
Key Concepts Covered:
- Linear Combination: Understanding how a linear combination of vectors can indicate independence. A vector is expressed as a weighted sum of others.
- Definition: A set of vectors is linearly independent if a linear combination that equals the zero vector has trivial solutions.
- Geometric Interpretation: Describes independence in two dimensions (R²) and three dimensions (R³), using the concepts of collinearity and coplanarity.
- Algebraic Criteria: Outlines a systematic method to verify linear independence through homogeneous systems of equations.
- Matrix Approach: Introduces Gaussian elimination as a tool to assess linear independence by examining pivot columns in a matrix representation of the vectors.
- Applications: Highlights practical uses in civil engineering, such as ensuring unique solutions in structural analysis.
This exploration aids both theoretical understanding and practical application for students in engineering fields, laying a strong foundation for further study in both mathematics and engineering disciplines.
Youtube Videos
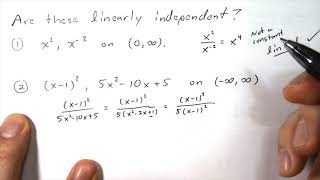
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Linear Independence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the study of vector spaces and systems of linear equations, the concept of linear independence plays a foundational role. It helps determine whether a set of vectors contains redundancy and whether they span a unique subspace. In civil engineering, linear independence is used in structural analysis, stability of structures, finite element methods, and solving systems of equations for unknowns in mechanical systems.
Detailed Explanation
Linear independence is crucial for understanding how vectors relate to one another in vector spaces. If a set of vectors is linearly independent, it means that no vector in that set can be expressed as a combination of the other vectors. Detecting redundancy in vectors ensures that calculations in engineering and physics are accurate and meaningful.
Examples & Analogies
Imagine you are trying to find your way around a city using a map. If you only have a few unique roads (vectors) that lead you to your destination, these roads are akin to linearly independent vectors. If you later discover that one road is just a rerouted version of another, then it adds redundancy, making navigation less efficient.
Definition of Linear Independence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A set of vectors {⃗v 1,⃗v 2,...,⃗v n} in a vector space V is said to be linearly independent if: a ⃗v + a ⃗v + … + a ⃗v = ⃗0 implies that a 1 = a 2 = … = a n = 0. Otherwise, the set is called linearly dependent. Key idea: If at least one vector in the set can be written as a linear combination of the others, the set is linearly dependent.
Detailed Explanation
This definition formalizes the concept of linear independence. If you can only achieve the zero vector by setting all coefficients (a1, a2, etc.) to zero, then the vectors are independent. If you can achieve the zero vector by using different values for the coefficients, then some vectors are dependent, as one can be represented by others.
Examples & Analogies
Consider a group of friends (vectors). If each friend can independently make their own decisions (linearly independent), then each one brings unique perspectives to the table. However, if one friend only echoes what another says, they add redundancy to the conversation (linearly dependent).
Algebraic Criterion for Linear Independence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To test whether a set of vectors is linearly independent: 1. Form a linear combination set equal to the zero vector. 2. Convert it to a homogeneous system of equations. 3. Solve the system: - If the only solution is the trivial solution (all coefficients = 0), the vectors are linearly independent. - If there exists a non-trivial solution, the set is linearly dependent.
Detailed Explanation
This chunk outlines a systematic approach to determine the independence of vectors. By creating equations that equal zero, it allows for an examination of the relationships between the vectors. If the only way to make the combination equal zero is by making all coefficients zero, the vectors are independent.
Examples & Analogies
Think of testing a recipe that symbolizes the vectors. If adding varying quantities of ingredients (coefficients) can lead to a dish that tastes like nothing (the zero vector), and the only way to get there is by not adding any ingredients at all, then you have an essential recipe (independent vectors). But if certain ingredients can be substituted without changing the flavor, those are non-essential (dependent vectors).
Geometric Interpretation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In R2: Two vectors are linearly independent if they are not collinear. Geometrically, they span a plane. In R3: Three vectors are linearly independent if they are not coplanar. They span the entire three-dimensional space.
Detailed Explanation
This chunk relates linear independence to geometry. In two dimensions, two vectors that do not lie along the same line (collinear) span a plane, meaning they can cover all points in that plane. In three dimensions, three vectors that do not lie on the same flat surface (coplanar) can fill the entire space.
Examples & Analogies
Visualize a plane with two vectors as arrows. If both arrows are pointing in the same line, they don’t cover any new area. However, if they point in different directions, they fill the entire plane like two roads diverging. In 3D, picture three pencils stuck in different directions that spread out and occupy the entire room.
Matrix Approach: Row Reduction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let ⃗v 1, ⃗v 2,..., ⃗v n be vectors in Rm, and form the matrix: A = [⃗v 1, ⃗v 2, ..., ⃗v n]. Steps: • Perform Gaussian elimination to reduce A to its row echelon form (REF). • Count the number of pivot columns: - If number of pivot columns = number of vectors → linearly independent. - If number of pivot columns < number of vectors → linearly dependent.
Detailed Explanation
This method uses matrices to determine linear independence. By applying Gaussian elimination, we streamline the matrix to a simpler form where we can easily count pivot positions (columns that lead the row). The number of these leading terms helps us conclude the independence of the original vector set.
Examples & Analogies
Think of organizing books on a shelf; each book represents a vector. You arrange them (row reduce) to see which shelves (pivot columns) are full. If every shelf is taken but you still have more books than shelves, some books are redundant and can be put together (dependence).
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Linear Combination: Understanding how a linear combination of vectors can indicate independence. A vector is expressed as a weighted sum of others.
-
Definition: A set of vectors is linearly independent if a linear combination that equals the zero vector has trivial solutions.
-
Geometric Interpretation: Describes independence in two dimensions (R²) and three dimensions (R³), using the concepts of collinearity and coplanarity.
-
Algebraic Criteria: Outlines a systematic method to verify linear independence through homogeneous systems of equations.
-
Matrix Approach: Introduces Gaussian elimination as a tool to assess linear independence by examining pivot columns in a matrix representation of the vectors.
-
Applications: Highlights practical uses in civil engineering, such as ensuring unique solutions in structural analysis.
-
This exploration aids both theoretical understanding and practical application for students in engineering fields, laying a strong foundation for further study in both mathematics and engineering disciplines.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of vectors [1, 2] and [2, 4] being linearly dependent due to collinearity.
-
Example of standard basis vectors in R^3 demonstrating linear independence.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If no vector stands alone, to zero they will moan; only zero's in control, if from theirs no others roll.
📖 Fascinating Stories
-
Imagine a team of superheroes; each can act alone. If one can cover others' roles, they are too similar and not independent.
🧠 Other Memory Gems
-
Remember the acronym 'LINE': Linear, Independent, Not Equal.
🎯 Super Acronyms
In BOLD
- Basis Of Linearly Dependent vectors.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Vector Space
Definition:
A set of vectors closed under vector addition and scalar multiplication.
-
Term: Basis
Definition:
A linearly independent set of vectors that spans the entire vector space.
-
Term: Linear Combination
Definition:
A vector formed by linear combinations of other vectors with associated scalars.
-
Term: Linearly Independent
Definition:
A set of vectors where the only linear combination that equals the zero vector has all coefficients equal to zero.
-
Term: Linearly Dependent
Definition:
A set of vectors where at least one vector can be written as a linear combination of others.