Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
The Importance of Maximal Linearly Independent Sets
Unlock Audio Lesson
Today, we are discussing maximal linearly independent sets. Can anyone tell me why identifying such sets is significant?
Is it because they help us understand the structure of vector spaces better?
Exactly! By focusing on maximal sets, we can simplify our analysis of vector spaces.
What does it mean for a set to be 'maximal'?
Great question! A maximal set is one that cannot add more vectors without becoming linearly dependent. It contains the maximum number of linearly independent vectors.
So, if I have a dependent set, I can find a maximal independent subset from it?
Precisely! We'll walk through the steps to extract that subset.
Let's summarize: A maximal linearly independent set is crucial for simplifying vector space analysis and understanding redundancies.
Algorithm for Extracting Maximal Independent Sets
Unlock Audio Lesson
Now, let's discuss the algorithm for extracting maximal independent sets. First, can anyone outline the steps?
Are we supposed to write the vectors in matrix form first?
That's correct! Start by expressing the vectors as columns in a matrix. What comes next?
Then we perform row reduction to get it to echelon form?
Exactly! Once we have the reduced form, we can identify the pivot columns. Can someone explain what pivot columns are?
They are the columns that contain the leading 1s in the row echelon form, right?
Great memory! The vectors corresponding to those pivot columns establish our maximal linearly independent set.
Just to recap: we extract the maximal independent subset by writing vectors in matrix form, reducing, and identifying pivot columns.
Applications of Maximal Independent Sets
Unlock Audio Lesson
How can the concept of maximal linearly independent sets apply in real-world scenarios?
I think it might help in optimization problems like the simplex method!
Absolutely! In optimization, we often need basis reduction, where understanding independent sets is vital.
What about more practical applications, like in technology?
Good point! In sensor networks, we can remove redundant sensors that provide predictable data from others, thereby maximizing efficiency.
So, identifying these sets helps in reducing complexity in data management?
Exactly! Efficient data management is just one application. To summarize: maximal independent sets find importance in both optimization and technological applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the process of identifying a maximal linearly independent subset from a dependent set of vectors using row operations and outlines its significance in various applications, including optimization and sensor networks.
Detailed
Maximal Linearly Independent Sets
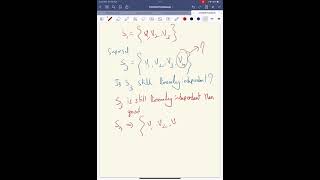
In linear algebra, maximizing the utility of a vector set is crucial. When dealing with linearly dependent vectors, we often need to extract the largest possible subset that remains linearly independent. This section outlines the steps to do so:
- Write the vectors as columns of a matrix.
- Perform row reduction to bring the matrix to echelon form.
- Identify pivot columns; the vectors corresponding to these columns form the maximal independent subset.
Understanding how to find maximal linearly independent sets is essential for applications in optimization (like basis reduction in the simplex method) and sensor networks, where eliminating redundant data sources is necessary.
Youtube Videos
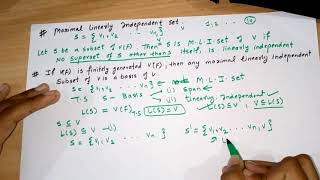
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Maximal Linearly Independent Sets
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Given a linearly dependent set of vectors, a maximal linearly independent subset can be extracted using row operations.
Detailed Explanation
In linear algebra, a maximal linearly independent set is a subset of vectors extracted from a larger set that is linearly dependent. This means that even though the original set has redundancies (some vectors can be expressed as combinations of others), we can find a smaller, independent group of vectors that retains the most information. To do this, we typically perform row operations on a matrix formed by placing the vectors as columns, which helps in identifying those vectors that contribute unique information.
Examples & Analogies
Think of a team project where many members can contribute ideas, but some ideas overlap or repeat. If you analyze all the suggestions, you might find that you only need a few unique ideas to cover everything. The unique ideas can be considered the maximal independent subset.
Algorithm for Extracting Maximal Sets
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Algorithm:
1. Write vectors as columns of a matrix.
2. Perform row reduction to echelon form.
3. Identify pivot columns — the corresponding vectors form the maximal independent set.
Detailed Explanation
This algorithm outlines the process for identifying a maximal linearly independent set from a linearly dependent collection of vectors. First, each vector is organized as a column in a matrix. Second, by employing row reduction to reach an echelon form, we can simplify the matrix to help reveal dependencies among the vectors. The pivot columns, which represent leading 1s in the rows of this reduced matrix, identify the vectors that can stand alone without being expressed in terms of the others. These pivot vectors collectively form the maximal linearly independent set.
Examples & Analogies
Imagine a group of musicians practicing together. Each musician plays an essential part in a song, but some parts may repeat. By writing down the music (akin to creating the matrix), you can simplify the score to show only distinct parts (the pivot columns) that make the music unique and harmonious, ensuring that each musician contributes an independent part.
Importance of Maximal Sets
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This concept is important in:
- Optimization problems: Basis reduction in the simplex method.
- Sensor networks: Removing redundant sensors whose data can be predicted by others.
Detailed Explanation
Maximal linearly independent sets are crucial in various fields, particularly in optimization and sensor networks. In optimization, especially within the simplex method, working with maximal independent sets simplifies problems and can lead to more efficient solutions. In technology, particularly in sensor networks, identifying and removing redundant sensors helps create more efficient data systems. Both applications rely on recognizing which components can operate independently to streamline processes and enhance performance.
Examples & Analogies
In an agricultural field equipped with multiple weather sensors, some sensors might collect similar data, making others unnecessary. By identifying and keeping only the independent sensors (the maximal independent set), farmers ensure that they gather the most accurate climate information without redundancy, thus making better decisions for crop management.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Maximal Linear Independence: A maximal linearly independent set cannot include additional vectors without becoming dependent.
-
Row Reduction: A method to simplify a matrix to determine characteristics like independence.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
To extract a maximal independent set from vectors {v1, v2, v3}, write them as columns in a matrix, perform row reduction, and determine pivot columns.
-
In a real-world scenario, sensor networks optimize data collection by identifying and removing redundant sensors based on their independence.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Maximal sets are neat and quick, independent vectors make them stick!
📖 Fascinating Stories
-
Imagine a toolbox where every tool is necessary; adding a redundant shovel would clutter the space, just as adding a vector to a maximal set can lose independence.
🧠 Other Memory Gems
-
PIVOT: 'Prioritize Independent Vectors; Organize Thoroughly' for remembering the importance of pivot columns.
🎯 Super Acronyms
M.I.S. stands for Maximal Independent Set—remembering what we want to achieve.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Maximal Linearly Independent Set
Definition:
A subset of vectors that is linearly independent and cannot include any additional vectors without losing this property.
-
Term: Pivot Column
Definition:
A column in a matrix that corresponds to a leading entry in the echelon form, indicating a linearly independent vector.