Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Wronskian
Unlock Audio Lesson
Today, we'll explore the Wronskian determinant, a critical method for testing linear independence among functions. Can anyone recall why linear independence is important?
It helps determine if functions can form a unique solution or not, right?
Exactly! If functions are linearly independent, it means they do not combine to form each other, leading to unique solutions. Let’s look at what the Wronskian actually is.
How do we actually compute the Wronskian?
Great question! The Wronskian is defined for a set of n functions as a determinant of a specific matrix. Let's go through the formula together.
Remember: if the Wronskian is non-zero for some value x, the functions are linearly independent! This is a key takeaway.
Calculating the Wronskian
Unlock Audio Lesson
Now that we understand the Wronskian's importance, let’s look at how to calculate it. For example, consider the functions f1(x) = x, f2(x) = x^2. Can we set up their Wronskian?
So, we create the determinant matrix with f1 and f2, and their derivatives?
Precisely! Their derivatives are f1'(x) = 1 and f2'(x) = 2x. What does the Wronskian look like?
"It would be:
Applications of the Wronskian in Engineering
Unlock Audio Lesson
Now that we can compute the Wronskian, let’s discuss its applications, especially in civil engineering. Can anyone suggest where this might be useful?
In beam deflection problems, for example!
Exactly! Ensuring the functions representing the deflections are linearly independent allows us to find a unique deformation profile in structures.
What about problems involving vibrations and soil mechanics?
Very relevant! Linear independence of solutions in those contexts ensures stability and validity of models. It’s fascinating how mathematics directly impacts engineering design!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the Wronskian determinant is defined and explained as a tool to ascertain whether a set of differentiable functions is linearly independent. It discusses its significance in engineering and provides applications relevant to civil engineering.
Detailed
Detailed Summary
The Wronskian determinant is a critical tool used in differential equations to test the linear independence of functions. Given a set of functions, denoted as f1(x), f2(x), ..., fn(x), that are differentiable up to order n-1, the Wronskian is constructed to assess their independence. The formula for the Wronskian is expressed as follows:
$$ W(f_1, f_2, \, ..., f_n)(x) = \begin{vmatrix}
f_1(x) & f_2(x) & \cdots & f_n(x) \
f_1'(x) & f_2'(x) & \cdots & f_n'(x) \
\vdots & \vdots & \ddots & \vdots \
f_{(n-1)}(x) & f_{(n-1)}(x) & \cdots & f_{(n-1)}(x)
\end{vmatrix} $$
The Wronskian is non-zero for at least one point in the interval if the set of functions is linearly independent. This concept is particularly valuable in civil engineering applications, as ensuring a unique solution in problems related to beam deflection and vibration requires linear independence of the solution functions. Thus, understanding the Wronskian is essential for developing reliable engineering models and structures.
Youtube Videos
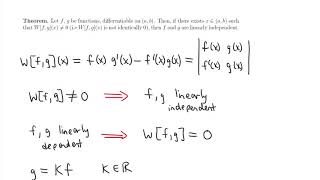
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of the Wronskian
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let f_1(x), f_2(x), ..., f_n(x) be functions differentiable up to order n−1. The Wronskian is defined as:
W(f_1, f_2, ..., f_n)(x) = | f_1(x) f_2(x) ... f_n(x) |
| f_1'(x) f_2'(x) ... f_n'(x) |
| ... ... ... |
| f_1(n−1)(x) f_2(n−1)(x) ... f_n(n−1)(x) |
Detailed Explanation
The Wronskian is a determinant that helps to test whether a set of functions is linearly independent. For n functions, the Wronskian is a matrix composed of the functions and their derivatives up to the (n-1)th order. The structure of the Wronskian is such that each row consists of the functions in the first row, their first derivatives in the second row, and so on, until the (n-1)th derivatives in the last row. Calculating the Wronskian involves finding the determinant of this matrix.
Examples & Analogies
Consider a team of scientists working on a complex project, where each scientist specializes in a different area. If their knowledge (functions) is unique and they do not overlap (independence), the collective outcome is much stronger. The Wronskian acts like a test to ensure each scientist can contribute uniquely to the project; if their contributions overlap too much, the team's effectiveness might diminish.
Testing Linear Independence with the Wronskian
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If W ≠ 0 for some x, the functions are linearly independent on that interval.
Detailed Explanation
To determine if the functions f_1, f_2, ..., f_n are linearly independent, you compute the Wronskian. If you find that the Wronskian is non-zero at some point x, it indicates that there is no way to write one of the functions as a linear combination of the others in that interval. This positive result confirms that the functions do not depend on one another in a linear sense.
Examples & Analogies
Think of different musical instruments in an orchestra. If each instrument (a function) contributes a unique sound (meaning it's necessary for the piece of music), the overall harmony (linear independence) is maintained. If one instrument can be replaced by another without loss, it indicates redundancy (linear dependence). The Wronskian here can be viewed as a ‘sound test’ to ensure all musicians play distinct notes.
Applications in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In civil engineering problems involving beam deflection, soil mechanics, or vibration, linear independence of solutions ensures a unique and physically valid deformation profile.
Detailed Explanation
In the field of civil engineering, especially in analyzing structures or systems, ensuring that solutions (functions) are linearly independent using the Wronskian is crucial. For instance, in calculating the deformation of beams under load, each unique deformation shape corresponds to an independent solution. If these solutions were linearly dependent, it would suggest that the structure could behave in multiple ways without a unique outcome, making it challenging to predict its response to loads.
Examples & Analogies
Imagine a bridge needing to flex under different loads; if the bridge's design relies on several methods of flexing (think of methods as functions), and those methods overlap too much, the bridge might not handle stress effectively, leading to potential failure. The Wronskian ensures these methods are unique, giving engineers confidence that each will contribute differently to the bridge's performance under various conditions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Wronskian: A determinant used to test if functions are linearly independent.
-
Linear Independence: A state where functions do not reproduce each other via linear combinations.
-
Differentiable Function: A function that has a derivative at every point in its interval.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For functions f1(x) = cos(x) and f2(x) = sin(x), the Wronskian W(f1,f2)(x) = 1, showing they are linearly independent.
-
In civil engineering, the linear independence of functions representing deflections in beams ensures structural integrity.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If W is not zero, then functions flow, independent from each other, as they grow.
📖 Fascinating Stories
-
Imagine a musician with different instruments. Each plays unique notes; if they tried to play the same note, it would create chaos! That’s what linear independence ensures for functions.
🧠 Other Memory Gems
-
Use the acronym 'WIP' to remember - Wronskian Indicates Independence of Functions.
🎯 Super Acronyms
WAF - Wronskian, Analyze, Functions for determining independence.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Wronskian
Definition:
A determinant used to test the linear independence of differentiable functions.
-
Term: Linear Independence
Definition:
A property of a set of functions where no function can be expressed as a linear combination of others.
-
Term: Determinant
Definition:
A calculated value that can determine properties of matrix, including whether a set of vectors is linearly independent.
-
Term: Differentiable Function
Definition:
A function that has a derivative at each point in its domain.