Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Explaining Orthogonality
Unlock Audio Lesson
Today we're going to talk about orthogonality. Can anyone tell me what two vectors being orthogonal means?
I think it means they don't overlap.
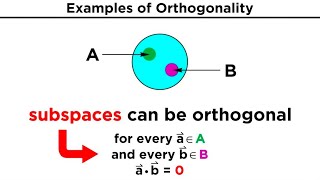
That's a good start! Orthogonality means that the dot product of two vectors is zero. This indicates that the vectors are at right angles to each other. Remember this: 'Orthogonal = Zero dot product'.
So if they're orthogonal, does that mean they are independent too?
Great question! Yes, if a set of vectors is mutually orthogonal and non-zero, it is indeed linearly independent.
Linking Orthogonality and Linear Independence
Unlock Audio Lesson
Let's connect these ideas. If we have vectors that are orthogonal, how might we show that they are linearly independent?
We can use the proof from the class, right? If we set up a linear combination that equals the zero vector, we'd take the dot product.
Exactly! By using the dot product with each vector, we find that all coefficients must be zero. This confirms the vectors are linearly independent.
Can you show us an example?
Sure! Consider vectors ⃗v1 = [1, 0] and ⃗v2 = [0, 1]. They are orthogonal since their dot product is 0, which means they're linearly independent.
Applications in Civil Engineering
Unlock Audio Lesson
Now that we understand the theoretical underpinnings, let’s discuss their applications in civil engineering. Can anyone think of a situation where this might be relevant?
Maybe in bridge design?
Exactly! Independent equations of equilibrium in structural analysis ensure that we can determine the forces acting in each member without redundancy.
What about when calculating modal shapes?
Great point! In modal analysis, mode shapes must be orthogonal to ensure unique and stable representations of structural behavior, which showcases the practical significance of these mathematical concepts.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains that a set of non-zero vectors is linearly independent if they are mutually orthogonal. It highlights applications in civil engineering, particularly in modal analysis and the least squares method, and introduces a proof idea to reinforce understanding.
Detailed
Orthogonality and Linear Independence
In linear algebra, the relationship between orthogonality and linear independence is crucial for understanding vector spaces. If a set of non-zero vectors is mutually orthogonal, this implies that it is linearly independent. This section explores this theorem and its implications in various applications, particularly in civil engineering.
Key Concepts:
- Orthogonality: Two vectors are orthogonal if their dot product is zero.
- Linear Independence: A set of vectors is linearly independent if the only solution to the linear combination equating to zero is the trivial solution (all coefficients are zero).
- Implications in Civil Engineering: The application of orthogonal vectors is crucial in modal analysis, where mode shapes are orthogonal, and in the least squares method, which simplifies calculations by utilizing orthogonal bases.
- Proof Idea: If vectors are orthogonal, taking the dot product with each vector in the set will show that all coefficients in the linear combination must be zero, confirming their linear independence.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Theorem of Orthogonality and Linear Independence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Theorem:
If a set of non-zero vectors is mutually orthogonal, then it is linearly independent.
Detailed Explanation
This theorem states that if we have a set of vectors that are orthogonal to each other (meaning each pair has a dot product of zero), they are automatically linearly independent. Linear independence means that no vector in the set can be expressed as a combination of the others. Orthogonality ensures that the vectors are distinctly pointing in different directions and thus cannot be expressed in terms of each other.
Examples & Analogies
Imagine a set of arrows pointing in completely different directions—like northeast, southeast, northwest, and southwest. No matter how you try to combine these arrows, you can’t replicate one arrow with others because they are all pointing different ways. Similarly, orthogonal vectors represent directions in a space that cannot 'collapse' into one another, ensuring their independence.
Significance in Numerical Methods
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is an especially important property in numerical methods.
Detailed Explanation
The importance of this property in numerical methods lies in the simplicity it brings to computations. When using orthogonal vectors, calculations become easier because the vectors do not influence each other. This means that algorithms can achieve greater accuracy and stability in calculations, particularly in fields like engineering and computer science.
Examples & Analogies
Think of this like simplifying a recipe. If each ingredient is distinct and does not react with others (like baking soda not reacting with flour), you can measure each one independently without worrying about how they might affect one another, making cooking simpler and the final dish more predictable.
Applications in Civil Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applications in Civil Engineering:
- Modal analysis: Mode shapes are orthogonal.
- Least squares method: Orthogonal basis simplifies calculations.
Detailed Explanation
In civil engineering, understanding and using orthogonality can enhance the analysis of structures. For instance, in modal analysis, the different mode shapes of structures like buildings are orthogonal, meaning that they can be analyzed separately without interference. In techniques like the least squares method, having an orthogonal basis allows engineers to compute results more efficiently, minimizing the errors that can occur when basis vectors overlap.
Examples & Analogies
Consider constructing a tall building. If the engineers can analyze each part—like the foundation, columns, and beams—independently without any interference from errors introduced in other parts, they can ensure the overall stability and safety of the building design, similar to studying different musical notes separately to create a harmonious symphony.
Proof Idea of Orthogonality Leading to Independence
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Proof Idea: Assume ⃗v 1,...,⃗v n are orthogonal. Consider the equation: a ⃗v +⋯+a ⃗v =0⃗
1 1 n n
Take dot product with ⃗v k, and use orthogonality to show all a k=0.
Detailed Explanation
The proof involves starting with the assumption that the vectors are orthogonal. By taking the dot product of a linear combination of these vectors that equals the zero vector with one of the vectors, you demonstrate that the coefficients for these vectors must all be zero. This is because if any coefficient were non-zero, the dot product could not equal zero due to the orthogonality condition.
Examples & Analogies
Envision a game of tug of war with teams pulling on ropes that lead in perfectly perpendicular directions. If there’s no movement (no net force), then it means that all individuals must be exerting no force of their own because each team's pull directly counters the others. Thus, just as each person’s effort needs to be zero for no movement to occur here, the proof confirms that all coefficients must be zero for the orthogonal vectors to sum to zero.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Orthogonality: Two vectors are orthogonal if their dot product is zero.
-
Linear Independence: A set of vectors is linearly independent if the only solution to the linear combination equating to zero is the trivial solution (all coefficients are zero).
-
Implications in Civil Engineering: The application of orthogonal vectors is crucial in modal analysis, where mode shapes are orthogonal, and in the least squares method, which simplifies calculations by utilizing orthogonal bases.
-
Proof Idea: If vectors are orthogonal, taking the dot product with each vector in the set will show that all coefficients in the linear combination must be zero, confirming their linear independence.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Two vectors ⃗v1 = [1, 0] and ⃗v2 = [0, 1] are mutually orthogonal and thus linearly independent.
-
Example 2: In a civil engineering context, mode shapes in vibration analysis are often orthogonal to facilitate accurate representation of deformations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Orthogonal, smart and 'zero-year', keeps vectors clear.
📖 Fascinating Stories
-
Imagine two lines at a crossroad, they never meet but shine bright, their angles are right.
🧠 Other Memory Gems
-
Remember: 'Orthogonal = O' = 'Zero dot product' where O stands for orthogonality.
🎯 Super Acronyms
OLI - 'Orthogonal Leads to Independence.'
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Orthogonality
Definition:
A property of vectors that indicates they are perpendicular to each other; mathematically defined by a dot product that equals zero.
-
Term: Linear Independence
Definition:
A set of vectors is linearly independent if the only linear combination of them that results in the zero vector is the trivial combination where all coefficients are zero.
-
Term: Dot Product
Definition:
An algebraic operation that takes two equal-length sequences of numbers and returns a single number; used to determine orthogonality.
-
Term: Mode Shapes
Definition:
The various patterns in which a structure can oscillate at each natural frequency without depending on other shapes.
-
Term: Least Squares Method
Definition:
A statistical method used to determine a line of best fit in data, often utilizing orthogonal bases for accuracy.