Summary Table: Quick Tests for Linear Independence
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Testing Vectors for Linear Independence
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to discuss how to quickly determine if a set of vectors is linearly independent using matrix row reduction. Can anyone tell me what we mean by 'linear independence'?

I think it means that no vector in the set can be expressed as a combination of the others.

Exactly! When we talk about vectors being linearly independent, we want to see if we can express one vector as a combination of others. To test this efficiently, we can row reduce the matrix formed from these vectors. What do you think we check for afterward?

We should look for the rank of the matrix?

Correct! If the rank equals the number of vectors, they are independent. It's a powerful test. Can anyone provide a real-world application of this concept in engineering?

In structural engineering, if the forces at joints are independent, it helps find a unique solution.

Great example! So remember, row reducing the matrix is a crucial test method for vector independence.

In summary, we use matrix row reduction to test if vectors are linearly independent by checking the rank.
Using the Wronskian to Test Functions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let’s move on to functions. Who knows what the Wronskian is?

Isn't it a determinant that helps us check if functions are linearly independent?

Exactly! The Wronskian is computed from the functions and their derivatives. If the Wronskian is non-zero for some point, what can we conclude?

Then the functions are linearly independent!

Right! It's a very useful tool, especially in differential equations. Can anyone think of when we might need this in engineering?

When modeling systems in vibrations, we need independent functions to describe behavior!

Perfect! So remember, the Wronskian is key to testing function independence, especially in engineering contexts.

To summarize, if the Wronskian is non-zero, the functions are linearly independent.
Orthogonal Vectors and Their Independence
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s talk about orthogonal vectors. We know that if vectors are orthogonal, they are linearly independent. Can anyone explain why?

Because if they're not pointing in the same direction and don’t overlap, you can't express one as the other!

Exactly! We can verify this by checking dot products. If the dot product of two different vectors is zero, they are orthogonal. What does that tell us?

That they are independent!

Correct! And this property can be very useful in areas like computer graphics and signal processing. Why do you think orthogonal sets are valuable?

They simplify calculations and avoid redundancy!

Well said! In summary, orthogonal vectors are linearly independent if they satisfy the dot product conditions.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The summary table provides methods for quickly assessing linear independence of vectors in Rn and functions using Wronskian, as well as evaluating structural equations. It emphasizes the importance of full rank for matrices and the conditions necessary for linear independence across various applications.
Detailed
Summary Table: Quick Tests for Linear Independence
The concept of linear independence is fundamental in linear algebra, particularly in determining the uniqueness of solutions in vector spaces. In this section, we outline quick tests and scenarios where these methods apply. Here’s a detailed breakdown:
| Scenario | Test Method | Result |
|---|---|---|
| Vectors in Rn | Row reduce matrix of vectors | Full rank → Independent |
| Functions | Wronskian = D | D ≠ 0 → Linearly independent |
| Orthogonal Vectors | Check dot products | All 0 (except with self) → independent |
| Structural Equations | Count unique equilibrium equations | ≤ DOF → Possibly independent |
This table simplifies the evaluation process and acts as a quick reference for students and professionals alike.
Youtube Videos





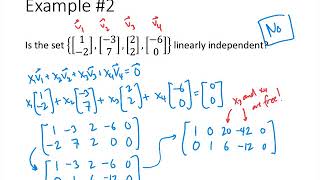

![[Linear Algebra] Linear Independence](https://img.youtube.com/vi/XI2kYIxhe-o/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Test for Vectors in Rn
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Vectors in Rn
Row reduce matrix of vectors
Full rank → Independent
Detailed Explanation
This chunk discusses how to determine if a set of vectors in n-dimensional space (Rn) is linearly independent by performing row reduction on their matrix. Row reduction involves applying a series of operations to transform the matrix into a simpler form, known as row echelon form. If the resulting matrix has full rank, meaning its rank equals the number of vectors, then the vectors are linearly independent. This implies that none of the vectors can be expressed as a linear combination of the others.
Examples & Analogies
Think of a team of workers in a project: if everyone has a unique skill that no one else has, the team as a whole can tackle various tasks without anyone stepping on anyone's toes. This uniqueness in skills is akin to vectors being linearly independent, meaning each vector contributes something new to the overall span of the vector space.
Test for Functions
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Functions
Wronskian = D ≠ 0
Linearly independent
Detailed Explanation
This chunk introduces the Wronskian determinant, a technique to test whether functions are linearly independent. The Wronskian is calculated from a matrix consisting of the functions and their derivatives. If the Wronskian is non-zero for some value of x, the functions are considered linearly independent, meaning no function in the set can be formed as a linear combination of the others. This concept is particularly useful in solving differential equations.
Examples & Analogies
Imagine a band where each musician plays a different instrument. Each musician's contribution is like a different function. If they play in harmony (i.e., none trying to reproduce someone else's part), the band sounds great together—just as linearly independent functions work in mathematical harmony without becoming redundant.
Test for Orthogonal Vectors
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Orthogonal Vectors
Check dot products
If all 0 (except with self), then independent
Detailed Explanation
This chunk explains how to check if a set of vectors is linearly independent by examining their dot products. If the dot product between each pair of different vectors is zero (and each vector dotted with itself is not zero), then the vectors are orthogonal and hence linearly independent. Orthogonality means that the vectors do not affect each other’s direction in space, contributing uniquely to the span.
Examples & Analogies
Think of navigating a city using streets that intersect at right angles. Each street represents a vector. If you travel down one street (vector) without getting in the way of others, each street can guide you to a different destination without redundancy—the streets (vectors) are orthogonal and independent.
Test for Structural Equations
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Structural Equations
Count unique equilibrium equations
≤ DOF → Possibly independent
Detailed Explanation
This chunk describes how to determine the linear independence of structural equilibrium equations by counting unique equations and ensuring they do not exceed the degrees of freedom (DOF) of the system. If the number of unique equilibrium equations is less than or equal to the available DOFs, it suggests that the system may have independent equations necessary for stability and proper function.
Examples & Analogies
Consider a bridge engineer designing a structure. Each equilibrium equation represents a safety check, like ensuring that forces are balanced. If they create more checks than the structure can handle (more equations than DOFs), it risks overspecifying the design, leading to inconsistencies. Just like too many cooks spoil the broth, too many redundant equations can complicate the structure's integrity.
Key Concepts
-
Testing Vectors: Row reduce matrices to determine independence by checking rank.
-
Using Wronskian: A determinant approach to assess linear independence of functions.
-
Orthogonality: Check dot products of vectors to confirm independence.
Examples & Applications
To test if vectors [1, 2] and [2, 4] in R2 are linearly independent, note that they are dependent as one is a scalar multiple of the other.
For functions f(x) = sin(x) and g(x) = cos(x), the Wronskian is non-zero, confirming they are linearly independent.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Vectors stacked in a row, full rank is what we know, if they can't combine, independence will show.
Stories
Think of a team of superheroes, each with unique powers – if one could replicate another, then they lose their strength together. That's what linear dependence feels like!
Memory Tools
To remember the steps: R.O.W. - 'Row reduction, Observe rank, Wronskian check!'
Acronyms
R.I.V.E.R - Rank indicates vectors' independent existence reliably.
Flash Cards
Glossary
- Linear Independence
A set of vectors or functions that cannot be expressed as a linear combination of one another.
- Rank of a Matrix
The maximum number of linearly independent row or column vectors in a matrix.
- Wronskian
A determinant used to test the linear independence of functions by evaluating their derivatives.
- Orthogonal Vectors
Vectors that are perpendicular to each other, implying linear independence.
- Full Rank
A condition where the rank of a matrix equals the number of its vectors, indicating linear independence.
Reference links
Supplementary resources to enhance your learning experience.
