Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Vector Spaces
Unlock Audio Lesson
Today, we are going to talk about vector spaces. Can anyone define what a vector space is?
Isn't it a set of vectors that can be added together and multiplied by scalars?
Exactly! A vector space is indeed a set closed under vector addition and scalar multiplication. This means if you take any two vectors in the space and add them, or multiply any vector by a scalar, you’ll get another vector in the same space. Remember the acronym 'CLOSED' — it stands for Closed under addition, Linear combinations, Operable.
What does 'operable' mean in this context?
'Operable' emphasizes that all operations are valid within the space. This is a fundamental property of vector spaces. Can someone give me an example of a vector space?
Could R^2 be an example?
Yes! R^2, the set of all ordered pairs of real numbers, is a classic example of a vector space.
Understanding Basis and Dimension
Unlock Audio Lesson
Now, let's talk about the basis of a vector space. What do we mean by a basis?
I think a basis is a set of vectors that spans the vector space.
That's right! A basis not only spans the space, but the vectors must also be linearly independent. Can anyone tell me why linear independence is essential?
If vectors are linearly independent, none of them can be written as a combination of the others, right?
Precisely! This means each vector contributes uniquely to the space, ensuring that there’s no redundancy. The number of vectors in the basis refers to the **dimension** of the vector space. Who remembers how to denote dimension?
It’s usually denoted as dim(V).
Exactly! Great job!
Importance of Linear Independence in Applications
Unlock Audio Lesson
Let’s connect these concepts to practical applications. How do we apply these ideas in civil engineering?
I think we need to ensure forces acting on structures are linearly independent for stable solutions.
Correct! If we have redundant forces, it could lead to complications in structural analysis. Remember, systems need **unique solutions** for stability. Can you think of a way this could be represented mathematically?
By forming linear combinations of the force vectors?
Exactly again! If those combinations lead to the zero vector only with trivial solutions, then we are good. Keep this in mind when analyzing structures!
Reviewing Key Concepts
Unlock Audio Lesson
To wrap up, can someone summarize what a vector space is?
It’s a set of vectors closed under addition and scalar multiplication.
Correct! And what about a basis?
A linearly independent set of vectors that spans the vector space.
Exactly! And one last question: why is linear independence significant?
It ensures unique representations in a vector space without redundancies.
Well done! Remember these key ideas as we move on to linear combinations next. You’ve all done great today!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The recap covers the definitions and key properties related to vector spaces, bases, and linear independence. It explains how vector spaces are structured and highlights the implications of linear independence when working with vectors, emphasizing its importance in contexts such as structural analysis in civil engineering.
Detailed
Vector Spaces and Basis (Recap)
In this section, we briefly review the foundational concepts of vector spaces and bases that set the stage for understanding linear independence. A vector space is defined as a set of vectors that is closed under vector addition and scalar multiplication, forming a structure where various operations can be performed. The basis of a vector space consists of a linearly independent set of vectors that spans the entire space, making it essential for representing vectors in that space.
The dimension of a vector space refers to the number of vectors in a basis, providing insight into the space's complexity.
Understanding these concepts is crucial not only in theoretical mathematics but also in practical applications, particularly in civil engineering. For instance, linear independence ensures that vectors used for structural analysis are not redundant, leading to unique and stable solutions.
Youtube Videos
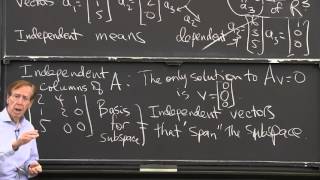
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of a Vector Space
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A vector space is a set of vectors closed under vector addition and scalar multiplication.
Detailed Explanation
A vector space is essentially a collection of vectors that can be added together and multiplied by numbers (scalars) while still remaining in the same collection. This means that if you take any two vectors in the space and add them, or if you multiply a vector by any number, the result is still a vector in that space. For example, consider the space of all 2D vectors (like arrows pointing in different directions). If you add two of them together or stretch or shrink one of them, you're still dealing with vectors that exist in the same 2D space.
Examples & Analogies
Think of a vector space like a basketball team. The players (vectors) can pass the ball (add vectors) to each other, and they can also change positions on the court (scalar multiplication), but they always remain part of the team (the vector space).
Understanding Basis of a Vector Space
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A basis of a vector space is a linearly independent set of vectors that spans the entire space.
Detailed Explanation
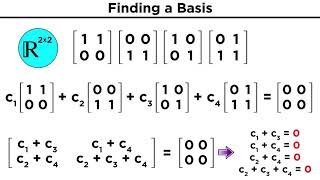
A basis comprises a specific collection of vectors that has two main characteristics. First, they must be linearly independent, meaning no vector in the set can be expressed as a combination of the others. Second, these vectors must span the entire vector space, which means that any vector in the space can be formed from these basis vectors through their linear combinations. For instance, in a 2D space, two non-collinear vectors can serve as a basis because you can reach any point in the space by combining these two vectors.
Examples & Analogies
Imagine you are trying to build any furniture (any vector in the space) using only wood planks (basis vectors) of distinct lengths. As long as you only use two lengths that aren't multiples of each other, you can create any piece of furniture by cutting and combining these planks in different ways (forming all possible vectors).
Dimension of a Vector Space
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The dimension of a vector space is the number of vectors in a basis.
Detailed Explanation
The dimension of a vector space gives us a numerical understanding of how much 'freedom' we have within that space. It is defined as the number of vectors in any basis of the vector space. For instance, if a space's basis consists of two vectors, its dimension is 2, indicating that two directions are needed to span that space. Higher dimensions indicate more complexity. A familiar example is 3D space having a dimension of 3, defined by three mutually perpendicular axes.
Examples & Analogies
Think of dimension like the number of ingredients needed for a particular recipe. If a dish requires three key ingredients (a basis), you need them to create various flavors (different vectors) in that dish. If you had only two, you would be limited in what you could make, which reflects the lower-dimensional space.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Vector Space: Defined as a closed set of vectors under operations of addition and scalar multiplication.
-
Basis: A collection of linearly independent vectors that spans the vector space.
-
Dimension: Count of the number of vectors in a basis that indicates the complexity of the space.
-
Linear Independence: A property of vectors that ensures unique representation in the span.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of a vector space is R^2, where elements are pairs of real numbers.
-
In R^3, three vectors are linearly independent if they are not coplanar.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a vector space, vectors align,
📖 Fascinating Stories
-
Imagine a receptionist (vector space) at a hotel. Each guest (vector) comes in, and they can multiply (scale) the number of guests without limits. Only a certain group (basis) of guests can represent all unique rooms in the hotel, ensuring no room is double-booked.
🧠 Other Memory Gems
-
Remember 'VBD' for vector space: Vectors, Basis, Dimension.
🎯 Super Acronyms
Use the acronym 'LIN' for Linear Independence
- Linear combinations result in Null only when Independent.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Vector Space
Definition:
A set of vectors closed under addition and scalar multiplication.
-
Term: Basis
Definition:
A linearly independent set of vectors that spans the vector space.
-
Term: Dimension
Definition:
The number of vectors in a basis, indicating the complexity of the vector space.
-
Term: Linear Independence
Definition:
A set of vectors is linearly independent if the only solution to their linear combination being zero is the trivial solution.
-
Term: Linear Combination
Definition:
A vector formed by using coefficients to sum a set of vectors.