Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Median in Discrete Series
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will learn about the median in discrete series. Does anyone know what a median is?
It's the middle value in a data set, right?
Exactly! The median divides the data into two equal halves. In a discrete series, we find the median using the cumulative frequency. Can anyone tell me how we locate the median's position?
Is it by using the formula (N + 1)/2?
That's correct! N is the total number of observations. This method helps us to pinpoint the median accurately.
Understanding Cumulative Frequency
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, let's discuss cumulative frequency. What does it mean?
I think it\u2019s the running total of frequencies in a data set.
Yes! Cumulative frequency helps us see how many observations fall below a certain point. It's essential for identifying where the median lies.
So how do we calculate it?
Great question! We add the frequency of each class interval to the sum of the previous frequencies. Let\u2019s look at an example to understand this better.
Calculating Median Income Example
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let\u2019s examine the income distribution we have: Income values and the number of persons. How do we begin?
First, we prepare the frequency table.
Correct! Then we need to calculate the cumulative frequency. Once we have that, how do we find the median?
We calculate the position using (N+1)/2.
Absolutely! In our example with 20 total respondents, the median position is 10.5. Now, what does that mean in terms of the cumulative frequency?
It means we look at the cumulative frequency of 16 because it covers the 10.5th observation!
Exactly! Therefore, the median income is Rs 30.
Practice Finding the Median
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now it's your turn! I have a new frequency distribution for you to analyze. Who wants to help me out?
I\u2019ll help! What\u2019s the distribution?
Assuming incomes of Rs 15, 25, 35, and 50 with frequencies of 3, 5, 7, and 2, first calculate the cumulative frequencies.
Let\u2019s see, cumulative frequencies would be 3, 8, 15, and 17.
Good job! Now, how do we find the median position?
It's (17+1)/2 = 9th observation.
Excellent! Now, which income value does the 9th observation correspond to?
It corresponds to Rs 35!
Perfect. You\u2019ve all done wonderfully today! You now have a better understanding of finding the median in a discrete series.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In discrete series, the median can be calculated using the cumulative frequency to find the (N+1)/2th observation. The example provided illustrates this process using income data, demonstrating how to locate the median value effectively.
Detailed
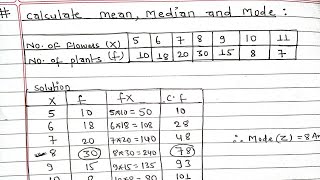
Discrete Series\n\nIn this section, we focus on calculating the median for a discrete series. The median is a vital measure of central tendency that represents the middle value of a data set. In the case of discrete series, the position of the median can be determined using the formula \n(N + 1)/2, where N is the total number of observations. By utilizing cumulative frequency, we can identify the value corresponding to this position to find the median.\n\n## Example: \nAn illustration is provided through an example calculating the median income based on a frequency distribution of income values. Here are the details:\n\n| Income (in Rs) | Number of Persons (f) | Cumulative Frequency (cf) |\n|----------------|-----------------------|---------------------------|\n| 10 | 2 | 2 |\n| 20 | 4 | 6 |\n| 30 | 10 | 16 |\n| 40 | 4 | 20 |\n\nThe median's position is computed as (20 + 1)/2 = 10.5, which corresponds to the cumulative frequency of 16. Thus, the income associated with this observation is Rs 30.\n\nThis exercise highlights the systematic approach to finding the median in a discrete series, illustrating fundamental principles of statistics in a practical setting.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding the Median in Discrete Series
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In case of discrete series the position of median i.e. (N+1)/2th item can be located through cumulative frequency. The corresponding value at this position is the value of median.
Detailed Explanation
In a discrete series, the median is calculated using the position of the data. Specifically, the position can be determined using the formula (N+1)/2, where N is the total number of observations. This formula provides the index of the median value when the data is ordered. Once we have the position, we can find the cumulative frequency, which helps locate the corresponding data value that represents the median.
Examples & Analogies
Imagine you're trying to find the median height of a group of children in a classroom. First, you count how many children are there (let's say 20). To find the median, you would calculate (20+1)/2 = 10.5, which means the median height is between the 10th and 11th tallest child. This process mimics using cumulative frequency to find your specific data point.
Example of Calculating Median Income
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example 7 The frequency distribution of the number of persons and their respective incomes (in Rs) are given below. Calculate the median income. Income (in Rs): 10 20 30 40 Number of persons: 2 4 10 4 In order to calculate the median income, you may prepare the frequency distribution as given below.
Detailed Explanation
In this example, we are given income levels and the corresponding number of people earning each income. To calculate the median income, we first set up a frequency distribution table. This provides a clear organizational view of how many people fall into each income category, which is essential for determining where the median lies. By preparing this table, we can easily compute cumulative frequencies, which help in finding the median value.
Examples & Analogies
Consider a fundraiser where you track donations from participants: $10 from 2 people, $20 from 4 people, $30 from 10 people, and $40 from 4 people. Just like tracking donations helps to see the range of contributions, compiling this income data allows us to find out the 'median contribution', indicating what a typical donor might have given.
Cumulative Frequency Table for Median Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
TABLE 5.5 Computation of Median for Discrete Series Income No. of Cumulative (in Rs) persons(f) frequency(cf) 10 2 2 20 4 6 30 10 16 40 4 20
Detailed Explanation
The cumulative frequency table shows how many people have an income less than or equal to each income level. This allows us to visualize the distribution of incomes. For example, for Rs 10, there are 2 people; for Rs 20, there are 6 people (2 from Rs 10 + 4 from Rs 20), and so forth. This step is crucial because the cumulative frequency lets us find the median observation's class quickly, which helps us determine the median income.
Examples & Analogies
Think of it like a race: you note how many runners have crossed certain checkpoints (income levels). The cumulative count shows you how many have completed the race at different stages, helping to identify the middle point where about half have finished.
Locating the Median Observation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The median is located in the (N+1)/2 = (20+1)/2 = 10.5th observation.
Detailed Explanation
To find where the median value sits, we calculate its position using our earlier formula. In this scenario, we find that the median position is the 10.5th observation. This means we look between the 10th and 11th observations in our cumulative frequency table to find the value that corresponds with the median income.
Examples & Analogies
Imagine splitting a group of 20 kids in a classroom to see who sits in the middle during a movie viewing. When you notice the 10th and 11th kids are the transition between the first and second halves, you'll find a representative 'middle kid' β this is like identifying our median income as we check the cumulative frequencies.
Determining the Median Income
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The 10.5th observation lies in the c.f. of 16. The income corresponding to this is Rs 30, so the median income is Rs 30.
Detailed Explanation
From our cumulative frequency table, the 10.5th observation falls in the cumulative frequency of 16, which indicates that the median income corresponds to an income value of Rs 30. This income level represents the middle point of the dataset, meaning half of the population earns less and half earn more.
Examples & Analogies
If you consider the median to be the point where half of the contributions are below and half above, then if Rs 30 is our midpoint, it's like saying that in a group of varying incomes, Rs 30 is an 'average' that balances many below and above it, just like the central position in a line of kids.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Median: The middle value of a data set when arranged in order.
-
Cumulative Frequency: The aggregate frequency that accumulates the total number of observations up to a certain point.
-
Discrete Series: A series in statistics where data points are distinct and separate.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating the median income from a distribution: 10, 20, 30, 40 with frequencies 2, 4, 10, 4 leads to a median income of Rs 30.
-
Using the cumulative frequency method helps visualize how observations are grouped supporting identification of the median.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
To find the median, just take a peek, at frequencies adding, that's the technique!
π Fascinating Stories
-
Once upon a time, in a land full of numbers, a wise old number named Median guided lost values to safety by helping them find their middle.
π§ Other Memory Gems
-
M is for Middle, E for Equal parts, D for Divide, I for Insight of values, A for Aggregate from frequency, N for Number of observations.
π― Super Acronyms
M-F-C
- Median - Frequency - Cumulative.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Median
Definition:
The value separating the higher half from the lower half of a data sample.
-
Term: Cumulative Frequency
Definition:
The sum of a class and all previous classes in a frequency distribution.
-
Term: Discrete Series
Definition:
A statistical representation of data points that can take only specific values.