Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mode
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will discuss the mode in a discrete series. Who can tell me what the mode represents?
Is it the most frequent value in the data set?
Exactly! The mode is the value that appears most often. For example, in the series 1, 2, 3, 4, 4, 5, can anyone tell me the mode?
It's 4! It appears twice.
Correct! Remember, the mode is not the only measure of central tendency. It can tell us about the distribution as well. Let's explore that more.
Types of Modes
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Modes can be classified into unimodal, bimodal, and multimodal. Can anyone explain what unimodal means?
It means there is only one mode, right?
Exactly! And what about bimodal?
That would be two modes.
Great! Now, multimodal means what?
More than two modes.
Correct! It's important to understand these classifications because they affect how we analyze data. Let's summarize.
Examples of Mode
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's look at a frequency distribution. For example, in the series with variables 10, 20, 30, 40, 50 and their respective frequencies, can someone identify the mode?
It's 30, right? Because 20 is the highest frequency.
Correct! Since there is a unique mode, this data is unimodal. But what if the frequencies were equal for two values?
Then it would be bimodal!
Exactly! Letβs recap what weβve learned about identifying and classifying modes.
Mode Absence
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Sometimes, we find data sets where no mode exists. Can someone tell me an example?
Like the series 1, 1, 2, 2, 3, 3, 4, 4?
Exactly! In that series, no number appears more frequently than the others. So, how do we classify this series?
It has no mode.
Correct! Understanding that sometimes, statistical measures can yield no result is crucial. Let's summarize everything we've learned about modes.
Recap and Review
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs recap. The mode is the most frequently occurring value. What are the types we discussed?
Unimodal, bimodal, and multimodal.
Correct! And can someone explain when there is no mode present?
When no single value appears more than others!
Perfect! Keep these concepts in mind as they are fundamental in statistics. Great job today, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the mode of a discrete series is explained, showcasing how it indicates the most frequently occurring value. Different types of data distributions, including unimodal, bimodal, and multimodal, are discussed along with examples, illustrating when a mode may not exist.
Detailed
Discrete Series
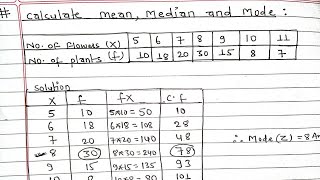
In statistics, the mode represents the most frequently occurring value in a data set. For instance, in the series 1, 2, 3, 4, 4, 5, the mode is 4 as it appears most frequently.
Example:
Consider the following discrete series:
- Variable: 10, 20, 30, 40, 50
- Frequency: 2, 8, 20, 10, 5
In this example, the maximum frequency is 20 at the variable 30, indicating it as a unimodal series, where a unique mode exists.
However, modes can be categorized further:
- Unimodal: One mode exists.
- Bimodal: Two modes exist.
- Multimodal: More than two modes exist.
- No mode: There might be instances, such as in the series 1, 1, 2, 2, 3, 3, 4, 4, where no value occurs more frequently than others, thus having no mode.
Youtube Videos
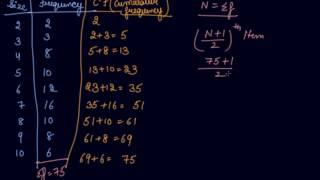
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Mode
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Consider the data set 1, 2, 3, 4, 4, 5. The mode for this data is 4 because 4 occurs most frequently (twice) in the data.
Detailed Explanation
In this example, the mode is defined as the number that appears most often in a data set. Here, we have the numbers 1, 2, 3, 4, 4, and 5. By counting how many times each number appears, we see that the number 4 appears twice, which is more than any other number. Therefore, we conclude that the mode of this data set is 4.
Examples & Analogies
Think of a classroom where students are voting for their favorite fruit: apples, oranges, bananas, and grapes. If more students choose apples than any other fruit, then apples are the 'mode' favorite. Just like in our data set, the mode tells us which choice is most popular.
Example with Discrete Series and Frequency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example 10 Look at the following discrete series: Variable 10 20 30 40 50 Frequency 2 8 20 10 5 Here, as you can see the maximum frequency is 20, the value of mode is 30. In this case, as there is a unique value of mode, the data is unimodal.
Detailed Explanation
In this chunk, we are presented with a table showing variables together with their corresponding frequencies. The variables (10, 20, 30, 40, and 50) represent different categories or values, while the frequencies (2, 8, 20, 10, and 5) represent how many times each value occurs. The number 30 has the highest frequency (20), making it the mode. Since there is only one highest frequency, we call this data 'unimodal', indicating it has one mode.
Examples & Analogies
Consider a bakery where different types of cupcakes are sold. After a day of sales, the cupcakes sold are counted: vanilla (2), chocolate (8), red velvet (20), lemon (10), and blueberry (5). The red velvet cupcakes sold the most, making them the 'mode' of that dayβs sales. This tells the bakery owner which flavors were most popular, simplifying restocking decisions.
Uniqueness of Mode in Data
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But, the mode is not necessarily unique, unlike arithmetic mean and median. You can have data with two modes (bi-modal) or more than two modes (multi-modal). It may be possible that there may be no mode if no value appears more frequent than any other value in the distribution.
Detailed Explanation
Unlike the mean and median, which provide a single central point in a dataset, the mode can vary in uniqueness. A dataset can have two modes, known as bi-modal, or even several modes, making it multi-modal. Additionally, there are cases where no mode exists if all values appear with the same frequency. For example, in a dataset like 1, 1, 2, 2, 3, 3, 4, 4, every number appears exactly twice. Consequently, there is no single mode because no number occurs more frequently than the others.
Examples & Analogies
Imagine a drawing competition where participants submit various designs. If two designs receive the highest votes equally, there are two winners - this is a bi-modal scenario. If all designs receive the same number of votes, thereβs no clear favorite, just like in a situation where there is no mode.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mode: The most frequently occurring value in a data set.
-
Unimodal: A series with a single mode.
-
Bimodal: A series with two modes.
-
Multimodal: A series with multiple modes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In the series 1, 2, 3, 4, 4, the mode is 4.
-
In the series of variables with frequencies 10, 20, 30, 40, 50, the mode is determined to be 30 since it occurs most frequently.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
If a number appears more than the rest, itβs the mode, itβs the best!
π Fascinating Stories
-
In a town of numbers, the number 4 hosted a party that every number attended twice! Therefore, everyone agreed that 4 was the mode among them.
π§ Other Memory Gems
-
M-U-B: Mode-Unique, Bimodal-2, Multimodal-3+.
π― Super Acronyms
M.U.M. β Mode, Unimodal, Multimodal.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mode
Definition:
The value that appears most frequently in a data set.
-
Term: Unimodal
Definition:
A distribution with only one mode.
-
Term: Bimodal
Definition:
A distribution with two modes.
-
Term: Multimodal
Definition:
A distribution with more than two modes.