Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Buoyancy
Unlock Audio Lesson
Today we explore buoyancy, which is a key topic in fluid mechanics. Can anyone tell me what buoyancy is?
Buoyancy is the force that makes things float!
Exactly! It's the upward force exerted by a fluid that opposes the weight of an object submerged in it. Archimedes' principle states that this buoyant force equals the weight of the fluid displaced by the object. Can someone explain why this is important?
It helps us understand how ships float and why some objects sink!
Right again! Remember: 'Buoyant Force = Weight of Fluid Displaced.' Now let's think about how we calculate the buoyant force using this principle.
Could you give an example of how to calculate it?
Certainly! If a block displaces 5 kg of water, the buoyant force acting on it is 5 kg, or approximately 49.05 Newtons. That's the force that keeps it afloat.
To summarize, buoyancy is the upward force that makes objects float and is quantified by the weight of the fluid displaced.
Understanding the Metacenter
Unlock Audio Lesson
Now that we know about buoyancy, let's discuss the concept of the metacenter. Who can tell me what the metacenter is?
Isn't it the point where the buoyant force acts?
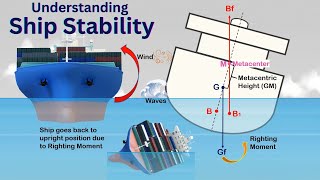
Exactly, Student_4! The metacenter is crucial for determining stability. When a floating object tilts, the center of buoyancy moves. If we find a point—called the metacenter—where the buoyant force acts, we can evaluate the stability of the object. How do you think this impacts the design of ships?
I suppose ships need to have a metacenter above the center of gravity to be stable?
That's correct! If the metacenter is above the center of gravity, the ship will return to its upright position after being tilted—this indicates stable equilibrium. If the metacenter is below, it would capsize, indicating unstable equilibrium.
Remember: 'Stable if Metacenter > Center of Gravity.' Anything else we should think about in ship design?
Maybe how much weight they carry or how they’re shaped?
Exactly! Weight distribution and hull shape affect the center of gravity and, subsequently, the metacenter. Keep this in mind!
Exploring Stability Concepts
Unlock Audio Lesson
Let's dive deeper into stability concepts: stable, unstable, and neutral equilibrium. Can anyone define stable equilibrium?
It's when a floating object returns to its original position after being tilted.
Right—an example would be a well-designed ship. What about unstable equilibrium?
That's when a small disturbance causes it to tip or capsize!
Exactly. In this case, the moment from the weight exceeds the restoring moment from the buoyancy. Lastly, what's neutral equilibrium?
That's when an object stays at its new position after being tilted.
Wonderful! Understanding these types of equilibrium helps engineers design safer vessels and structures. Always relate stability to the positions of the CG and CB!
Impact of Rigid Body Motion
Unlock Audio Lesson
Now let's connect our discussion to rigid body motion of objects in fluids. Can anyone tell me how rigid body motion might affect pressure in a fluid?
Perhaps the motion changes the pressure distribution?
Yes! As objects rotate uniformly, they create pressure gradients in the fluid. Can we think of a relatable example?
Like a spinning top or a water mixer?
Excellent examples! When a top spins, water around it experiences varying pressures. This concept is significant in fluid systems and affects everything from ship design to mechanical pumps.
In summary, remember that rigid body motion influences pressure distribution, which is crucial for fluid dynamics.
Recap and Applications
Unlock Audio Lesson
As we wrap up, who can recap what we learned about buoyancy and stability?
We learned about buoyancy and its relation to weight displacement as well as how stability relates to the metacenter!
Great summary! How might these principles apply in the real world, say, in boat design?
Boats have to be designed to keep their metacenter above their center of gravity.
Exactly! Proper design keeps vessels safe and reduces capsizing risks. These principles apply beyond boats too: in oil rigs, submarines, and more!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the principles of buoyancy as described by Archimedes, understand the significance of the metacentre in determining stability, and examine how rigid body motion affects pressure distribution in fluids. Through detailed explanations and examples, we aim to clarify the interactions between forces acting on submerged and floating objects.
Detailed
Buoyancy, Metacentre, Stability, and Rigid Body Motion
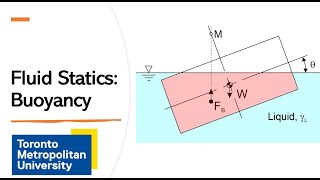
In fluid mechanics, buoyancy is a crucial concept derived from Archimedes' principle, which states that any object submerged in a fluid experiences an upward buoyant force equal to the weight of the fluid it displaces. This section delves into the mechanics of buoyancy and introduces the metacenter, which is essential for assessing the stability of floating bodies. The metacenter is defined as the point where the upward buoyant force acts and it plays a critical role in determining whether a floating object will return to its original position after being tilted.
When discussing stability, we distinguish between stable, neutral, and unstable equilibria, emphasizing how a floating object's center of gravity (CG) and center of buoyancy (CB) must relate for stability. A floating body is in stable equilibrium if, after being displaced, it experiences a restoring moment that brings it back to its original position. Conversely, it is in unstable equilibrium if a small displacement causes it to capsize.
Lastly, we touch on rigid body motion and its impact on liquids, discussing how pressure distribution can change during uniform angular rotations, displaying the complexities of fluid behavior under various conditions.
This section is foundational for civil and mechanical engineering applications, highlighting the essential principles that guide the stability of ships, submarines, and various fluid-carrying structures.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Buoyancy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us go to the next levels. We will discuss today the concept of the buoyancy, very well known Archimedes principles. In that we will also discuss it the metacenter or metacentric height how to determine the metacentric height of a floating object. And we also will talk about the stability of the floating object.
Detailed Explanation
In this chunk, the lecture introduces key concepts of buoyancy, which is the upward force experienced by objects submerged in fluids, and references Archimedes' principle, a foundational idea in fluid mechanics. It outlines the importance of understanding the metacenter, which helps in assessing the stability of floating bodies, as well as the general principles that govern their behavior in fluids.
Examples & Analogies
Think about a toy boat in a bathtub. When you place the boat on the water, it floats because the water pushes up against it with a force equal to the weight of the boat. This upward push—buoyancy—keeps the boat afloat, illustrating Archimedes' principle.
Understanding Archimedes' Principle
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Archimedes principle states that a body immersed in fluid experiences a vertical buoyant force equal to the weight of the fluid displaced by that body.
Detailed Explanation
Archimedes' principle is vital in fluid mechanics as it explains why objects float or sink in fluids. When an object is submerged, it pushes down a certain volume of fluid. The weight of the fluid displaced exerts an upward force on the object, known as buoyant force. If this force is greater than the weight of the object, it will rise; if less, it will sink.
Examples & Analogies
Imagine a balloon filled with helium. When you let it go, it rises in the air because the weight of the air it displaces is greater than the weight of the balloon; this is a real-world application of Archimedes' principle.
Center of Buoyancy and Gravity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The line of actions of the buoyant force is the center of buoyancy. That means at which point the buoyancy force acts.
Detailed Explanation
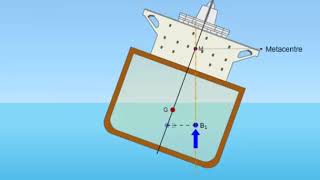
The center of buoyancy is the centroid of the volume of fluid displaced by the submerged part of the object. This point is crucial because it is where the buoyant force acts. For an object to float stably, the center of buoyancy must be directly below the center of gravity. If these two points align vertically, the object remains stable. If they do not, the object may tilt.
Examples & Analogies
Consider a seesaw in a playground. If one side is heavier and low, it tilts. Similarly, if the center of gravity and the center of buoyancy are misaligned, the floating object will experience tilting, potentially leading to instability.
Stability of Floating Objects
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To understand the stability of a floating object, the concepts of natural, stable, and unstable equilibrium are crucial.
Detailed Explanation
An object is in stable equilibrium when it returns to its original position after a slight tilt due to a restoring force. In contrast, if it tips over and does not return to its initial position, it is in unstable equilibrium. Natural equilibrium is a special case where it remains unchanged with small disturbances.
Examples & Analogies
Think of a person balancing on one leg. If they sway a bit and can easily regain balance, they are in stable equilibrium. If they fall over, they are in unstable equilibrium. In a similar manner, ships and boats are designed to maintain a stable equilibrium to prevent capsizing.
Metacentre and Metacentric Height
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If a floating object tilts, the center of buoyancy shifts, and the metacenter is the point at which the buoyant force acts when an object is tilted.
Detailed Explanation
The concept of metacentric height (BM) is essential for stability analysis in floating bodies. It is the vertical distance between the center of gravity (G) and the metacenter (M). A larger metacentric height means better stability. If BM is greater than BG (the center of gravity height), the object is stable. If BM is less than BG, it can lead to capsizing.
Examples & Analogies
Imagine a tall tower versus a short, wide building. The tall tower is more likely to sway in a strong wind and may topple compared to the short, wide building, which has a lower center of gravity and can resist tipping, analogous to how metacentric height influences a ship's stability.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Buoyancy: The upward force opposing an object's weight in a fluid.
-
Metacenter: The point that determines the stability of floating objects.
-
Stable Equilibrium: When an object returns to its original position after disturbance.
-
Unstable Equilibrium: When an object capsizes after a disturbance.
-
Fluid Pressure Distribution: The different pressures exerted by fluids in motion or under rigid body movement.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A ship floating in water experiences an upward force equal to the weight of the water it displaces, which keeps it afloat.
-
A swimmer changes their body position to maintain balance in the water, demonstrating the principle of buoyancy.
-
An iceberg displaces water equivalent to its weight; its stability depends on its center of gravity and buoyancy.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When a ship tips to the sea, the metacenter sets it free, if above CG it will sway, back to the path, on its way.
📖 Fascinating Stories
-
Imagine a ship on the ocean, enjoying the waves. As it tilts, the metacenter guides it back upright, just like a dancer returning to balance after a spin.
🧠 Other Memory Gems
-
B.M.G. - Buoyancy, Metacenter, Gravity - Remember these to understand stability.
🎯 Super Acronyms
B.S.M.
- Buoyancy
- Stability
- Metacenter - Key concepts to memorized for fluid mechanics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Buoyancy
Definition:
An upward force exerted by a fluid that opposes the weight of an object submerged in it.
-
Term: Archimedes' Principle
Definition:
The principle stating that a body immersed in a fluid experiences a buoyant force equal to the weight of the fluid displaced by the body.
-
Term: Metacenter
Definition:
The point where the upward buoyant force acts on a floating object, crucial for determining its stability.
-
Term: Equilibrium
Definition:
A state of balance where forces acting on an object result in no net force, determining its stability.
-
Term: Center of Gravity (CG)
Definition:
The point at which the weight of a body is concentrated, influencing its stability.
-
Term: Center of Buoyancy (CB)
Definition:
The centroid of the displaced volume of fluid, acting as the effective force location of buoyancy.
-
Term: Stable Equilibrium
Definition:
Condition where a slight disturbance causes a body to return to its original position.
-
Term: Unstable Equilibrium
Definition:
Condition where a slight disturbance causes a body to move away from its original position, potentially leading to capsizing.
-
Term: Neutral Equilibrium
Definition:
Condition where a body remains in its new position after being disturbed.