Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Buoyancy
Unlock Audio Lesson
Today we will explore the concept of buoyancy, which is essential in fluid mechanics. Could anyone tell me what buoyancy means?
Is it the upward force that makes objects float in a fluid?
Exactly, great answer! Buoyancy is the upward force exerted by a fluid at rest that counters the weight of a submerged object. It can be explained through Archimedes' principle. Can anyone summarize this principle?
Archimedes’ principle states that a body immersed in a fluid experiences an upward buoyant force equal to the weight of the fluid displaced.
Spot on! Remember: 'Buoyant force = weight of fluid displaced.' A mnemonic to remember this is 'B = W' for Buoyancy equals Weight.
What happens if the buoyant force is less than the weight of the object?
Good question! If the buoyant force is less, the object will sink. Now, let's move on to center of buoyancy.
To summarize, buoyancy allows objects to float or sink, depending on the upward force compared to their weight.
Equilibrium Types
Unlock Audio Lesson
Now that we understand buoyancy, let's discuss equilibrium types. Who can explain the differences?
There's stable, unstable, and neutral equilibrium, right?
Correct! In stable equilibrium, if disturbed, the object returns to its original position. Can anyone provide an example?
A buoyant boat might bob back to upright when tilted.
Exactly! Now, what about unstable equilibrium?
That’s when a small disturbance causes the object to capsize or move away from the original position.
Right! It’s important to know when designing ships to avoid instability. Lastly, can someone summarize neutral equilibrium?
In neutral equilibrium, the object stays where it was disturbed, neither returning nor tipping over.
Great summary! Remember: stable brings back, unstable tips away, neutral stays still.
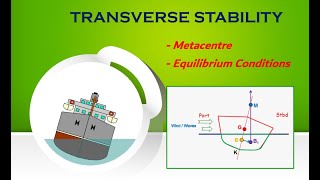
Center of Gravity and Metacentric Height
Unlock Audio Lesson
Today, we’re examining the center of gravity and metacentric height. Who can define these terms?
The center of gravity is the average position of weight in an object, and metacentric height determines stability.
Exactly! The metacentric height is crucial for ensuring a floating object's stability. Can someone explain its significance?
If the metacentric height is greater than the distance to the center of gravity, the object is stable.
Perfect! An easy way to remember this is 'M > G means stable.' What happens if M < G?
Then it becomes unstable and may capsized.
Good! Remember: M and G relationship determines stability.
Real-Life Applications of Stability
Unlock Audio Lesson
Finally, let's apply what we've learned to some real-life scenarios. Think about a ship's design. Who can tell me why stability matters?
If a ship capsizes, it can lead to disaster and loss of lives.
Yes! Designers must calculate metacentric heights for safety. Any famous examples where stability was crucial?
The Titanic crash was partly due to stability issues!
Exactly! Understanding these principles can prevent such tragedies. Let's wrap up our key insights about stability.
In summary, buoyancy affects stability, with the relationship between metacentric height and center of gravity being crucial.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In the study of fluid mechanics, this section emphasizes the significance of buoyancy, Archimedes’ principle, and the distinction between stable, unstable, and neutral equilibrium in floating bodies. It introduces how the concepts of center of gravity and center of buoyancy affect the stability of objects in a fluid.
Detailed
Detailed Summary
Introduction
This section of the fluid mechanics chapter discusses buoyancy, a fundamental concept explained by Archimedes' principle, which states that a body submerged in a fluid experiences an upward buoyant force equal to the weight of the fluid displaced.
Buoyancy and Force Components
When an object is submerged in a fluid, two forces act on it: the upward buoyant force and the downward gravitational force due to its weight. The difference in these forces determines whether an object will float, sink, or remain neutrally buoyant.
Center of Buoyancy and Center of Gravity
The center of buoyancy is the point where the buoyant force can be considered to act, typically at the centroid of the displaced fluid volume. For an object to be stable, the center of gravity must be located in relation to the center of buoyancy, affecting the object's stability.
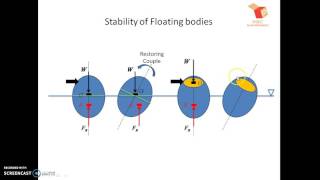
Types of Equilibrium
- Stable Equilibrium: Here, if the object is disturbed, it returns to its original position, as the metacentric height (distance between the center of buoyancy and the metacenter) is greater than the distance to the center of gravity.
- Unstable Equilibrium: In this case, any disturbance causes the object to move further away from its original position, leading to capsizing if metacentric height is less than the distance to the center of gravity.
- Neutral Equilibrium: The object remains in its new position post-disturbance, occurring when the center of buoyancy and center of gravity align.
Calculating Metacentric Height
The section also delves into calculating metacentric height, critical in ship design and stability analysis, to ensure that floating bodies maintain equilibrium in varying conditions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Stability of Floating Objects
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us come back to the topics what we have been discussing that fluid at the rest. As I told it when the fluid is at rest we have the two force components. One is force due to the pressure and the second is the gravity force. There is no velocity components, there is no shear stress component. So that is the reasons if you take a control volumes, it is easy to draw the pressure diagrams and from that pressure diagrams, if you equate with the gravity force, you can solve the problems.
Detailed Explanation
In fluid mechanics, when we talk about floating objects, we often refer to their stability. Stability is defined by how an object responds when it is disturbed. For any floating body, there are two main forces acting on it: the buoyant force (upward force due to fluid displacement) and the weight of the object (downward force). In a stable floating condition, if you slightly tilt or disturb the object (say, a ship), the forces will work together to bring it back to its original position. Conversely, if these forces do not balance correctly, the object may capsize or become unstable.
Examples & Analogies
Consider a toy sailboat on a pond. If the wind hits it and tilts the boat, if the buoyant force is greater than the weight, it will right itself because those forces push it back up. If you pushed it too far and the sail got wet (making it heavy), it might capsize, showing instability.
Understanding Metacenter
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
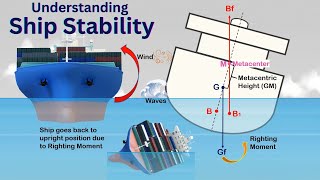
Let me introduce one point, which is we call the metacenters, okay. That is what is called the metacenter. What is that metacenters, okay? If I tilt a floating object to an angle of delta theta, then there will be a new waterline that comes. The center of buoyancy will change from B to Bprime as the waterline changes, and along that, you will have the buoyancy force that is going to act.
Detailed Explanation
The metacenter is a crucial point for understanding the stability of floating bodies. When an object is tilted, its center of buoyancy shifts due to the change in the waterline. The metacenter is defined as the point where the vertical line through the center of buoyancy meets the original waterline after tilting. If this metacenter is above the center of gravity (CG) of the object, the object is considered to be in a stable equilibrium because the restoring forces will correct any tilting.
Examples & Analogies
Imagine a seesaw (teeter-totter) where one side is heavier but positioned well. When someone pushes it down, if the pivot (analogous to the metacenter) is correctly placed, the seesaw will return to its resting position. If the pivot is too low (metacenter below the center of gravity), it may flip entirely, just as a boat would capsize.
Types of Equilibrium
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So let me summarize that, that when you have a floating object to test its stability, we generate a small disturbance of tilted at a small angle Δθ. The theoretically, if the BM and BG (distance between buoyancy and metacentric height) are having the relationship like BM > BG or BM < BG we have a stable or unstable equilibrium.
Detailed Explanation
There are generally three types of equilibrium: stable, unstable, and neutral. In stable equilibrium, if the object is disturbed, it returns to its original position, whereas in unstable equilibrium, any disturbance causes the object to tilt further from its original position, potentially leading to capsizing. Neutral equilibrium means the object stays in its new position after being disturbed. Understanding these distinctions helps when designing ships and other floating bodies to ensure safety.
Examples & Analogies
Think about balancing a pencil on your finger. If you can balance it perfectly (neutral equilibrium), it doesn’t fall but it doesn't return to your finger if it’s nudged. If you push it slightly and it falls down (unstable equilibrium), you’ll need to reposition it. If you place it on something wide enough to not fall (stable equilibrium), it stays put even if bumped.
Calculating Metacentric Height
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now how to compute this the metacentric height? Let you have a floating object. What we will do is take the area of the moment of inertia of the waterline about the axis of tilting to find out how we can establish a relationship between the metacentric height.
Detailed Explanation
To determine whether a floating object is stable, we calculate the metacentric height (GM). This involves understanding the geometry of the submerged part of the object. The moment of inertia, which accounts for how mass is distributed, helps in calculating how buoyancy interacts with the object’s weight when tilted. If the spacing from metacenter (M) to center of gravity (G) is large, the object is likely to be stable.
Examples & Analogies
If you picture a tall building, it has a high center of gravity (maybe compared to a wide one-story building). The taller it is, the easier it is to topple. The same goes for boats: a wide boat with low CG will be more stable in the water than a tall, narrow boat. Those calculations help find the ideal design for safety.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Buoyancy: The upward force opposing weight in a fluid.
-
Archimedes' Principle: Displaced fluid weight equals buoyant force.
-
Metacentric Height: Determines floating stability.
-
Equilibrium Types: Classifications include stable, unstable, neutral.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A submerged cube experiences an upward buoyant force equal to the weight of the water displaced.
-
A ship returning to its upright position after being slightly tilted illustrates stable equilibrium.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If something floats and holds its place, buoyancy gives it the right space.
📖 Fascinating Stories
-
Imagine Archimedes in his bathtub—every time he splashed, he noticed how objects behaved in water, discovering the magic of buoyancy.
🧠 Other Memory Gems
-
Boys Always Measure Stable Heights (Buoyancy, Archimedes' principle, Metacentric height, Stability).
🎯 Super Acronyms
BAM
- Buoyancy And Metacentric for stability.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Buoyancy
Definition:
The upward force exerted by a fluid that opposes the weight of an object immersed in it.
-
Term: Archimedes' Principle
Definition:
A principle stating that an object submerged in a fluid experiences a buoyant force equal to the weight of the fluid it displaces.
-
Term: Metacentric Height
Definition:
The distance between the center of gravity and the metacenter, influencing the stability of floating objects.
-
Term: Center of Gravity (CG)
Definition:
The point in a body where the total weight of the body may be considered to be concentrated.
-
Term: Stable Equilibrium
Definition:
A state of balance where an object returns to its original position after being disturbed.
-
Term: Unstable Equilibrium
Definition:
A state where any disturbance causes an object to move away from its original position, potentially leading to capsizing.
-
Term: Neutral Equilibrium
Definition:
A state where an object remains in its disturbed position without returning or tipping over.