Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Basic Forces in Fluids
Unlock Audio Lesson
Welcome, class! Today we will explore the fundamental forces acting on a fluid at rest. Does anyone know what these forces might be?
Is it the pressure from above and the force of gravity?
Exactly! We mainly consider pressure and gravitational force. Pressure in fluids increases with depth. Remember the phrase 'depth means pressure,' or DMP for short!
How does pressure actually change with depth?
Great question! The pressure at a depth h in a fluid can be calculated using the equation P = ρgh, where ρ is the fluid density and g is the acceleration due to gravity.
So, the deeper we go, the greater the pressure?
Absolutely! Now let's draw a simple pressure diagram for visual aid. Pressure increases linearly as we go deeper. This is crucial for calculating forces on submerged surfaces.
Can we see how this pressure affects buoyant forces?
Yes, buoyant force is essential! It can be simply explained by Archimedes' principle which states that a body submerged in a fluid experiences an upward force equal to the weight of the fluid displaced.
To summarize, we discussed the definition of pressure in fluids and the role it plays in buoyancy. DMP is a good memory aid for understanding how depth affects pressure!
Buoyant Forces
Unlock Audio Lesson
Now that we've established what pressure is, let's dig deeper into buoyancy. Who can tell me what buoyant force is?
I think it's the force that makes objects float.
Yes! The buoyant force acts upward against the weight of the submerged object. It is essential for understanding why items float or sink.
So, how is this buoyant force calculated?
The buoyant force can be calculated by the formula F_b = ρ_fluid * V_displaced * g, where V_displaced is the volume of the fluid displaced by the object. Always remember the relationship: it's about the volume of fluid displaced.
What’s the relation of this force to the object’s weight?
That’s crucial: if buoyant force equals the object’s weight, the object will float. If it is less, the object sinks. A nice way to remember this is 'Floating equals Balancing!'
That's a catchy phrase!
To summarize, we covered the buoyant force and its dependence on the weight of the fluid displaced and how this affects object stability. Remember 'Floating equals Balancing!' as your guide!
Metacenter and Stability
Unlock Audio Lesson
Next, let's talk about stability in floating objects and how the metacenter plays a role in this. Who knows what the metacenter is?
Is it the point that helps determine stability?
Excellent! The metacenter is the point where the buoyant force acts when an object is tilted. This is essential in determining whether an object is in stable, unstable, or neutral equilibrium. Remember the acronym M-G for Metacenter-Gravity!
How does one make sure an object is stable?
Good point! For stability, the metacenter needs to be above the center of gravity. If M is above G, it's stable. If G is above M, it's unstable. You can think of it as 'M must rise above G for safety!'
Interesting! What happens during a tilt?
When tilted, the center of buoyancy shifts, but if M remains above G, the object returns to its original position, ensuring stability. It's all about balance.
This is fascinating, especially with regards to ship design.
Indeed! To summarize, we discussed the metacenter and the requirement for it to be above the center of gravity for stability. Use 'M must rise above G for safety!' to help you remember!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Fluid statics deals with the forces in a fluid at rest, primarily focusing on pressure from gravity and its implications for buoyancy. The section covers key concepts such as pressure diagrams, forces on curved surfaces, and the significance of buoyancy and metacenters in determining the stability of floating objects.
Detailed
Forces in a Fluid at Rest
In this section, we delve into fluid statics, which examines the forces acting within a fluid that is at rest. The two primary forces to be analyzed are pressure, governed by depth and the density of the fluid, and the gravitational force acting on the fluid mass. The segment further explores how these forces manifest in real-world applications, particularly buoyancy and its effects on stability within floating objects, like ships or submerged bodies.
Key topics include:
- Pressure Distribution: Understanding how pressure varies with depth, represented visually through pressure diagrams.
- Forces on Curved Surfaces: Analyzing how to resolve forces acting on surfaces that are not flat, including the implications of these forces in engineering applications.
- Buoyancy and Archimedes' Principle: Highlighting Archimedes' insights regarding buoyant forces acting on submerged objects and their practical importance in various contexts.
- Metacenter and Stability: Investigating the concept of the metacenter, which relates to the stability of floating bodies, and how the relationship between the center of gravity and buoyancy affects equilibrium states.
These principles form the foundation for understanding more complex fluid interactions in both natural and engineered systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Basic Forces in a Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As I told it when the fluid is the rest we have the two force component. One is force due to the pressure and the second is the gravity force. There is no velocity components, there is no shear stress component.
Detailed Explanation
When a fluid is at rest, it experiences two main forces: the force due to pressure acting in all directions and the gravitational force acting downward. Since the fluid isn't moving, there aren't any velocity or shear stress components to consider, simplifying our analysis of the fluid's behavior.
Examples & Analogies
Think of a swimming pool filled with water. When no one is splashing around and the water is perfectly still, the only forces acting on the water at any given point are the weight pushing down due to gravity and the pressure from the surrounding water pushing up. It's like a calm lake on a sunny day.
Determining Forces on a Curved Surface
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you have to determine what could be the forces on a curved surface? What the problems we face it. If you have a let me take this example. So you have the free surface and you have a curved surface and you have the liquid which is having the density let be the rho.
Detailed Explanation
To analyze the forces acting on a curved surface submerged in a fluid, we must consider that pressure acts normally (perpendicularly) at each point of the surface. As pressure varies with depth, we break the curved surface into smaller flat segments. By integrating these forces across the surface, we can calculate the total force exerted on the curved surface.
Examples & Analogies
Imagine submerging a basketball in a swimming pool. The water applies pressure on the ball both from the top and the sides, and this pressure increases the deeper the ball goes. By understanding how this pressure works at various points on the ball, engineers can design stronger balls that can withstand this force even at deeper waters.
Pressure Diagrams for Curved Surfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So that is the reasons if you take a control volumes, it is easy to draw the pressure diagrams and from that pressure diagrams, if you equate with the gravity force, you can solve the problems.
Detailed Explanation
Creating pressure diagrams allows us to visualize how pressure changes across the surface of a submerged structure. By equating these pressures with gravitational forces acting on the fluid, we can solve for unknown forces. This method is helpful in analyzing how the structure will respond to the pressures it encounters.
Examples & Analogies
Think about a snorkeling experience. When you're underwater, you can feel the pressure of the water on your body. If you were to draw a diagram showing how the pressure changes with depth while you're underwater, you would see that it increases the further down you go. This knowledge helps engineers design diving equipment that can safely withstand these pressures.
Resolving Forces into Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The problems come it that we can simplify that ones like we can resolve the curved surface into a two-part horizontal and vertical components.
Detailed Explanation
To make calculations easier, we can resolve the total force acting on a curved surface into horizontal and vertical components. By doing this, we can separately analyze the upward buoyant forces and downward gravitational forces, simplifying our problem-solving process.
Examples & Analogies
Imagine trying to lift a large balloon underwater. The balloon has an upward force due to buoyancy and a downward force due to its weight. By breaking these forces down into vertical (up and down) and horizontal (side to side) components, you can figure out how much assistance you may need to lift it out of the water.
Understanding Buoyant Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As you know it the famous scientist Archimedes what invented this buoyancy concept when he was in a bathtub experienced the lighter weight because of the buoyancy forces.
Detailed Explanation
Archimedes' principle states that any object submerged in a fluid experiences an upward buoyant force equal to the weight of the fluid it displaces. This principle helps us understand why objects feel lighter in water than in air, as the water pushes up against the object, counteracting some of its weight.
Examples & Analogies
Consider an ice cube in a glass of water. The cube floats because it displaces a volume of water equal to its weight. As it floats, the water level rises to accommodate the weight of the cube, showcasing Archimedes' principle in action.
Center of Buoyancy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look it another point is we also look it that the center of buoyancy. That means the line of actions of the buoyant force is the center of buoyancy.
Detailed Explanation
The center of buoyancy is the point through which the buoyant force acts, and it is located at the centroid of the displaced fluid volume. Understanding where this point is relative to the center of gravity of the object is crucial for stability. A stable floating object has its center of buoyancy above its center of gravity, ensuring it right itself when tilted.
Examples & Analogies
Think of how a cork floats. The cork naturally turns upright in water because its center of buoyancy is above its center of gravity. If you push it under the water, it will want to come back up – this restoration is all about the relationship between the center of buoyancy and gravity.
Summary of Archimedes' Principle
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To summarize and to make it very easy to say that the Archimedes principles what it says that a body immersed in a fluid experience a vertical buoyant force.
Detailed Explanation
To recap, Archimedes' principle asserts that an object immersed in a fluid will experience an upward buoyant force equal to the weight of the fluid displaced by the object. This principle is fundamental in understanding why we float or sink in water.
Examples & Analogies
A good example is when you’re at the beach. When you walk into the water, you feel your weight decrease. This feeling is the buoyant force from the water pushing up against you, demonstrating Archimedes' principle.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
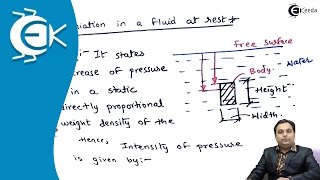
Pressure increases with depth in a fluid due to the weight of the fluid above it.
-
Buoyant force is equal to the weight of the fluid displaced by an object.
-
The metacenter is critical for analyzing the stability of floating objects.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When a boat is floating on water, the weight of water displaced by the boat's hull equals the weight of the boat. This means its buoyant force is balanced, allowing it to float.
-
In a pool, when a swimmer dives, they displace some water, and the upward buoyant force they experience is equal to the weight of the water displaced.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In water deep where pressures grow, buoyant force will surely show!
📖 Fascinating Stories
-
Imagine a boat gently floating; it rides high on the waves thanks to the water it displaces, heavier than itself!
🧠 Other Memory Gems
-
Remember 'M-G' to think of the Metacenter above Gravity for stability.
🎯 Super Acronyms
Use the acronym B.H.B.
- Buoyant rises from Heavier Bodies!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fluid Statics
Definition:
The study of fluids at rest and the forces acting on them.
-
Term: Buoyant Force
Definition:
The upward force exerted by a fluid on a submerged object, equal to the weight of fluid displaced.
-
Term: Metacenter
Definition:
The point where the buoyant force acts when an object is tilted, crucial for understanding stability.
-
Term: Center of Gravity
Definition:
The point where all weight of an object is considered to act, influencing balance.
-
Term: Pressure
Definition:
The force exerted per unit area; in fluids, pressure increases with depth.