Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Buoyancy
Unlock Audio Lesson
Today, we're discussing the principle of buoyancy, rooted in Archimedes' discovery. Can someone explain what buoyancy means?
Buoyancy is the upward force that a fluid exerts on an object submerged in it.
Exactly! This force equals the weight of the fluid displaced by the object. Now, why is understanding this important in fluid mechanics?
It helps us determine whether an object will float or sink.
Correct! Now, let’s remember this with the acronym 'B.E.S.T' — Buoyant force Equals the weight of the Submerged fluid in volume Tangent. Let’s proceed to the concept of the metacenter.
Metacentric Height Explained
Unlock Audio Lesson
Can anyone tell me what the metacentric height (GM) is?
Isn't it the distance between the center of gravity and the metacenter?
Exactly! Understanding GM is crucial for assessing the stability of floating objects. When GM is greater than BG, the object will return to its original position after tilting. Can anyone explain what BG represents?
It’s the vertical distance from the center of gravity to the center of buoyancy.
Well done! To help us remember, think of the phrase 'Good Mates Balance'—indicating that we must balance G and M to ensure stability.
Equilibrium Conditions
Unlock Audio Lesson
Now that we know about buoyancy and metacentric height, let's discuss the types of equilibrium. What are the three types of stability we can expect in floating objects?
Stable, unstable, and natural equilibrium!
Correct. Can someone explain stable equilibrium?
In stable equilibrium, the floating object returns to its equilibrium position after a disturbance, like a boat righting itself after a wave.
Good. An unstable equilibrium flips over with any disturbance. Remember 'UP & DOWN' — Under Pressure, unstable, or not stable leads to capsizing! Let’s summarize what we learned.
Calculating Metacentric Height
Unlock Audio Lesson
Let's move on to how we calculate metacentric height (GM). Can someone explain the basics?
We need the volume that's submerged and the vertical distance from G to the center of buoyancy.
That's right! Also, we can derive the formula from the moment of inertia of submerged surfaces. What's one of the key relationships here?
The relationship between the metacentric height and the center of gravity determines whether the object will return to equilibrium.
Exactly! To remember the calculation process, use 'VOLUME PITCHING' — Volume, Orientation, and Mathematically Evaluate the Pitch. Let’s recap what we’ve learned in this session.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on the principles of buoyancy as formulated by Archimedes and explores the concept of metacentric height, which is critical for assessing the stability of floating objects. It also introduces the equilibrium conditions for floating bodies.
Detailed
Detailed Summary of Metacentric Height
In this section, we explore the concept of metacentric height (GM), a crucial factor in determining the stability of floating bodies. The discussion begins with Archimedes' principle of buoyancy, which states that any object submerged in a fluid experiences an upward buoyant force equal to the weight of the fluid displaced. This principle lays the groundwork for understanding stability in floating systems.
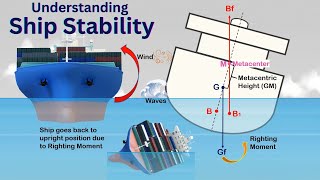
We analyze how the center of buoyancy (B) shifts depending on the object's position in the fluid, particularly when tilted. The movement of the center of buoyancy leads to a new line of action for the buoyant force (FB), and the relative positions of the center of gravity (G) and the metacenter (M) dictate whether an object remains stable or tips over.
- Stable Equilibrium: When GM (metacentric height) is greater than BG (vertical distance from G to B), the object tends to return to its original position after a disturbance.
- Unstable Equilibrium: Conversely, if GM is less than BG, the object is at risk of capsizing because any disturbance causes it to tip further.
To calculate GM, one must consider the submerged volume of the body, the moment of inertia regarding the buoyant force, and the area of the waterline. The section concludes by emphasizing the practical applications of this knowledge in engineering, particularly in ship design and other buoyant structures.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Metacenter and Stability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
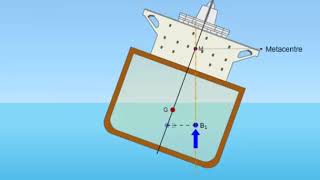
Now let us discuss about the stability of floating object, stability of floating objects like the ship. How much stability we have a floating objects. Now let us understand the principles the how the concept is conceived. As we discussed that there will be a gravity force which will act the CG of the floating object and there will be the force which is a buoyant force will act as the CG of the displaced liquid that what will be the center of buoyancy.
Detailed Explanation
This chunk introduces the basic concept of stability for floating objects, especially ships. The stability of a floating object depends on the relationship between two critical points: the center of gravity (CG) of the object and the center of buoyancy (CB) of the displaced liquid. The gravity force acts downwards at the CG, while the buoyant force acts upwards at the CB. It’s the distance between these two points and their relationship that determines the stability of the floating object: if the buoyant force is above the center of gravity, the object will tend to return to its original position if disturbed (stable equilibrium).
Examples & Analogies
Think of a seesaw in a park. If one child is heavier and sitting further from the center, the seesaw tilts and stabilizes when the lighter child sits closer to the center. This stability is similar to how the buoyancy and gravity work on a floating ship. If the buoyant force (like the lighter child) is positioned higher than the CG (the heavier child), the ship can return to balance if it tips.
The Concept of Metacentric Height (BM and BG)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now how to compute this the metacentric height? Let you have a floating object like this, okay? And you consider the unit width of this ones which is a perpendicular to this surface that is what unit width is there. So what we will do it let have the initial positions of waterlines goes through this C to D. So initially it was C to D and it was tilted okay. Because of the tilting as I explained earlier the B changes to B’.
Detailed Explanation
The metacentric height (BM) is the vertical distance between the center of gravity (G) and the metacenter (M), the point where the buoyant force acts when the body is tilted. To compute this, you analyze the geometry of the floating body, examining how the center of buoyancy shifts when the body tilts. Initially, the waterline and center of buoyancy are established at points C and B. As the object tilts, the center of buoyancy moves to point B'. The difference in height between the two centers determines the metacentric height, which is a critical factor for stability.
Examples & Analogies
Imagine a ship navigating through waves. When the ship tilts, the point as to where the buoyant force acts also shifts. If the metacenter is sufficiently above the center of gravity, the ship will right itself, much like how a balance beam will return to horizontal when it is moved slightly off position.
Equilibrium Conditions: Natural, Stable, and Unstable
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So to summarize and to make it very easy to say that Archimedes principles what it says that a body immersed in a fluid experience a vertical buoyant force. That means whenever you immerse a body in a fluid, you will have a vertical buoyant force will act it which will be equal to weight of the fluid displayed by the body and the buoyant force act upward through the centroid of the displaced volume.
Detailed Explanation
Archimedes' principle is foundational to understanding buoyancy. The principle states that any submerged object experiences an upward buoyant force equal to the weight of the fluid displaced. This is key to finding equilibrium conditions. There are three types of equilibria: natural equilibrium, stable equilibrium, and unstable equilibrium. In stable equilibrium, if the body is disturbed, it returns to its original position; in unstable equilibrium, any disturbance causes a greater tilt leading to a potential capsize. Understanding these conditions helps design ships that maintain balance in waves and currents.
Examples & Analogies
Think of a beach ball floating on water. If you push it under the water, it bobs back to the surface (stable equilibrium). Now, if you try to balance it vertically on its side, the moment you let go, it will fall over (unstable equilibrium). The balance of forces is crucial in both instances.
Calculating the Metacentric Height
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look it the first, the moment of this part, volume part we have considered aOBde that means this part, okay? That is what will be the three components will be there. Because of this, this component will be the minus, this component will be positive. That is what is happened. cOBd will be the positive and this way. Since this is the axis of symmetry, these values becomes zero.
Detailed Explanation
The calculation of metacentric height involves using principles of volume and moments. You analyze the volume displaced by the floating object and apply concepts of center of gravity and center of buoyancy. By integrating the geometry of the body and the moments of the buoyant forces, it is possible to mathematically express the relationship, allowing for the determination of the metacentric height. This process can rely on symmetrical properties of the object to simplify calculations.
Examples & Analogies
Consider balancing a ruler on your finger. Depending on how far from the center you hold it, it either falls or balances. In fluid dynamics, mathematicians and engineers calculate where to support a ship to keep it balanced, similarly considering the distribution of weight in water and using mathematical tools to ensure it stays upright.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Buoyancy: The force that allows objects to float in fluids.
-
Metacentric Height (GM): Measures the stability of a floating body.
-
Center of Gravity (G): The balancing point of an object.
-
Center of Buoyancy (B): Acts as the centroid of displaced fluid.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A ship can float due to the buoyant force exerted by the water, guided by principles like metacentric height and center of gravity.
-
When tilting a boat, the center of buoyancy shifts, affecting the metacentric height and determining stability.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When boats desire to float high, their center of gravity must be nigh.
📖 Fascinating Stories
-
Imagine a brave little fish swimming with its friends, knowing it won't flip because of its safe buoyancy and smart metacentric design.
🧠 Other Memory Gems
-
To remember buoyancy relations, use 'BG Mates Feel Safe' for buoyancy, gravity, metacenter, and stability.
🎯 Super Acronyms
M.G.B. — Metacenter, Gravity, Buoyancy for remembering key terms.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Buoyancy
Definition:
The upward force exerted by a fluid on a submerged object.
-
Term: Metacentric Height (GM)
Definition:
The distance between the center of gravity and the metacenter of a floating body.
-
Term: Center of Gravity (G)
Definition:
The point through which the weight of a body acts.
-
Term: Center of Buoyancy (B)
Definition:
The centroid of the submerged volume of fluid displaced by a floating object.
-
Term: Stable Equilibrium
Definition:
Condition under which a floating object returns to its original position after a disturbance.
-
Term: Unstable Equilibrium
Definition:
Condition where a disturbance to the floating object leads it to tip over.