Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluids at Rest
Unlock Audio Lesson
Today, we will explore fluids at rest. Can anyone tell me the two main forces acting on a fluid when it is not moving?
Is it the pressure force and gravitational force?
Exactly! Pressure forces act uniformly in all directions, while gravity acts downwards. This balance leads to interesting phenomena like buoyancy. What happens to a submerged object in a fluid?
It experiences an upward buoyant force.
Correct! This brings us to Archimedes' principle, stating that any submerged body displaces a volume of fluid equal to the weight of the object. Remember, the acronym 'B.O.A.T' - Buoyant force = Overturned weight = Archimedes' Principle = Ton of fluid displaced. Keep that in mind!
Understanding Buoyancy
Unlock Audio Lesson
Let's discuss buoyancy further. Why do you think understanding buoyancy is critical in fields like engineering?
It's important for designing ships and other floating structures.
Correct! Buoyancy helps engineers design vessels that stay afloat. When an object is afloat, the weight of the liquid displaced equals its weight. Can anyone summarize how we determine the buoyant force using a practical example?
We calculate it by measuring the weight of the fluid displaced, which depends on the object's volume and the fluid's density.
Well said! Let's summarize that: Buoyant force can be calculated using the formula: B = ρ_fluid × V_displaced × g.
Metacentric Height and Stability
Unlock Audio Lesson
We are now advancing to the concept of metacentric height. Who can explain what stability means in the context of floating objects?
It's how resistive an object is to tipping over when disturbed.
That's right! Stability is crucial. The location of the metacenter compared to the center of gravity defines the stability. Can anyone tell me what happens if the center of buoyancy shifts and the metacenter is below the center of gravity?
It can become unstable and capsize.
Exactly! If BM < BG, the object is unstable. Remember the mnemonic 'G.B.M.' - Gravity overcomes Buoyancy if Metacenter is lower.
Could you explain how we calculate metacentric height?
Of course! We measure the distance between the center of buoyancy and the metacenter. Understanding this helps engineers create stable floating designs.
Applications of Fluid Statics
Unlock Audio Lesson
Let’s relate these concepts to real-world applications, specifically in naval engineering. How does knowledge of buoyancy help in designing ships?
It helps in ensuring that ships can float and carry loads safely.
Great! And how about submarines? What's their buoyancy strategy?
Submarines can adjust their buoyancy by taking in water to dive or expelling water to surface.
Exactly! By adjusting their buoyancy, they manipulate their position in the water. Always remember the principle of floatation in design: Buoyant force must equal weight to float.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into the fundamentals of fluid mechanics while focusing on fluids at rest. The primary topics include the buoyancy force, Archimedes' principle, the concepts of the center of buoyancy, and the metacentric height necessary for determining the stability of floating bodies, showcasing their importance through real-world applications.
Detailed
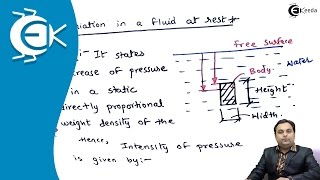
Fluid at Rest
In this section, we examine the critical principles of fluid mechanics related to static fluids. The two primary forces acting on fluids at rest include pressure force and gravitational force, with no shear stress components. A major highlight is Archimedes' principle, which states that any object submerged in a fluid experiences an upward buoyant force equal to the weight of the fluid displaced by the object. This principle illustrates the relationship between buoyancy and stability, which is vital in applications such as ship design. We define key terms like the center of buoyancy, which is the point through which the buoyant force acts, and metacentric height, which determines the stability of floating objects. Understanding the stability of floating bodies involves analyzing their center of gravity and center of buoyancy to ascertain if they return to equilibrium when tilted. This foundational knowledge is significant in engineering applications, particularly in naval architecture.
Youtube Videos
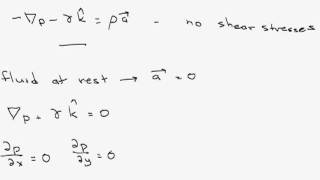
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Fluid at Rest
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us come back to the topics what we have been discussing that fluid at the rest okay. As I told it when the fluid is at rest, we have two force components. One is the force due to pressure and the second is the gravity force. There are no velocity components, and there is no shear stress component.
Detailed Explanation
In fluid mechanics, a fluid at rest experiences two primary forces: the pressure force and the gravitational force. When we say that a fluid is at rest, it means that it is not moving, so we do not consider any effects of velocity or shear stress. This simplifies the analysis of forces acting on the fluid. The pressure force acts uniformly in all directions and is dependent on the depth of the fluid, while gravity is constant. The balance of these forces determines the behavior of the fluid in static conditions.
Examples & Analogies
Think of a still pond of water. In this case, the water does not move. The water exerts pressure downwards due to its weight, and gravity pulls it downwards. There are no currents, waves, or disturbances, much like how a book rests flat on a table without sliding off.
Forces on Curved Surfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
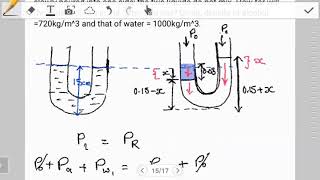
Now if you look it if you have to determine what could be the forces on a curved surface? If you take any point, as you know it the pressure is a scalar quantity, and will have the pressure component normal to the point where you were considering the surface.
Detailed Explanation
When analyzing forces on curved surfaces submerged in fluid, it is essential to understand how pressure varies at different points due to the curvature. Pressure acts perpendicular to any surface, and because the surface is curved, the pressure direction changes at different points. To compute the total force acting on the curved surface, we can resolve it into components along three axes (x, y, z) and integrate over the entire surface. Simplifying the analysis often requires breaking the curved surface down into vertical and horizontal components for easier calculations.
Examples & Analogies
Imagine a balloon that is partly submerged in water. The water exerts pressure on the balloon's surface. Since the balloon is curved, the pressure at the bottom of the balloon is higher than at the top. To find out how much force the water is pushing on the balloon, we consider those differences in pressure as we calculate the total force acting on the balloon's surface.
Understanding Buoyancy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to very interesting topics what is we use in buoyancy as you know it the famous scientist Archimedes what invented this buoyancy concept when he was in a bathtub experienced the lighter weight because of the buoyancy forces.
Detailed Explanation
Buoyancy refers to the upward force that a fluid exerts on an object submerged in it, which was famously described by Archimedes. According to his principle, the buoyant force is equal to the weight of the fluid displaced by the object. Thus, when an object is placed in a fluid, it experiences a force upward that makes it feel lighter. If the weight of the object is less than the buoyant force, it will float. If it is more, it will sink. The key to buoyancy is understanding that this force acts through the center of buoyancy, which is located at the centroid of the displaced fluid volume.
Examples & Analogies
Consider a rubber duck floating in a bathtub. The rubber duck is displacing water equal to its weight. If the weight of the duck is less than the weight of the water it displaces, it floats. If you were to add weights to the duck until it becomes heavier than the water it displaces, it would begin to sink. This balance of forces is fundamental to understanding buoyancy.
Center of Buoyancy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look at another point, we also look at the center of buoyancy. That means the line of actions of the buoyant force like we try to compute for the other force component.
Detailed Explanation
The center of buoyancy is the theoretical point where the buoyant force acts, and it is located at the centroid of the displaced volume of fluid. This point is crucial in determining the stability of floating or submerged bodies. In practical scenarios, the center of buoyancy shifts depending on the orientation and shape of the underwater object, affecting whether it maintains balance or tips over. If the center of buoyancy is not aligned with the center of gravity, the object may rotate or capsize.
Examples & Analogies
Think of a swimmer trying to float. When a swimmer is horizontal in the water, their center of gravity is aligned well with their center of buoyancy, allowing them to stay balanced. However, if they tilt or move in a way that shifts either one, they may start to tip over unless they adjust their body to restore balance.
Equilibrium of Floating Objects
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us understand the principles of the stability of floating objects. There will be gravity force which will act at the CG of the floating object, and there will be the force which is the buoyant force acting as the CG of the displaced liquid...
Detailed Explanation
Floating objects can be in three states of equilibrium: natural, stable, or unstable. Natural equilibrium occurs when the center of gravity and center of buoyancy are both in the same vertical line, allowing the object to remain in a balanced position regardless of slight disturbances. Stable equilibrium is when any small disturbance will cause the object to return to its original positioning, due to the buoyant force producing a restoring torque. Conversely, unstable equilibrium is when any small disturbance leads to a tipping point, causing the object to capsize. These concepts are critical when designing ships or other floating vessels to ensure their safety and stability.
Examples & Analogies
Picture a small boat on a lake. If it is perfectly upright and a gust of wind hits it but the boat stays upright and corrects itself, it is in stable equilibrium. However, if the boat tips slightly and continues to tip further until it capsizes, it is in unstable equilibrium. Understanding these states can be akin to balancing a pencil on your finger; if it's perfectly vertical, it will stay upright. But even a slight tilt will send it crashing down.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Buoyant Force: The upward force on submerged objects equal to the weight of the fluid displaced.
-
Archimedes' Principle: A principle stating a body submerged in fluid will experience a buoyant force equal to the weight of fluid displaced.
-
Center of Buoyancy: The point at which buoyant force acts, determined by fluid displacement.
-
Metacentric Height: A critical distance that determines the stability of floating objects in fluids.
-
Center of Gravity: The point through which the weight acts and influences stability.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A ship floating on water experiences a buoyant force that equals its weight, allowing it to stay afloat.
-
A submerged stone displaces an equal volume of water, resulting in an upward buoyant force that can lift it if submerged completely.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In water, you may feel light, thanks to buoyancy's rising might!
📖 Fascinating Stories
-
Imagine a swimmer lying back in a pool; the water lifts them gently, making them feel as if they float effortlessly on a pillow of liquid, illustrating the beauty of buoyancy.
🧠 Other Memory Gems
-
B.O.A.T - Buoyant force, Overturned weight, Archimedes' principle, Ton of fluid displaced!
🎯 Super Acronyms
G.B.M. - Gravity overcomes Buoyancy if Metacenter is lower.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Buoyant Force
Definition:
The upward force experienced by an object submerged in a fluid, equal to the weight of the fluid displaced.
-
Term: Archimedes' Principle
Definition:
A principle stating that a body immersed in a fluid experiences a buoyant force equal to the weight of the fluid displaced.
-
Term: Center of Buoyancy
Definition:
The centroid of the displaced volume of fluid, where the buoyant force acts.
-
Term: Metacentric Height (BM)
Definition:
The vertical distance between the center of buoyancy and the metacenter; it assesses a floating object's stability.
-
Term: Center of Gravity (CG)
Definition:
The point where the total weight of an object acts, influencing its stability.