Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Buoyancy and Archimedes' Principle
Unlock Audio Lesson
Today we will discuss buoyancy, largely defined by Archimedes' principle. Who can tell me what buoyancy means?
Isn't buoyancy the force that makes objects feel lighter in water?
Exactly! Buoyancy is the upward force exerted by fluids that opposes the weight of an object. So, according to Archimedes' principle, what can we say about the buoyant force on a submerged object?
The buoyant force equals the weight of the fluid displaced by the object.
Correct! Remember the acronym **B.F.W.D.** - Buoyant Force = Weight Displaced. Let’s summarize: Every object submerged in a fluid displaces some of that fluid. The weight of the displaced fluid determines the buoyant force.
Understanding the Center of Buoyancy
Unlock Audio Lesson
Now that we have covered buoyancy, let's talk about the center of buoyancy. What does this refer to?
Is it the point where the buoyant force acts?
Yes, it is! The center of buoyancy is the centroid of the displaced volume of the fluid. When an object is submerged, the buoyant force acts through this point. Why do you think this is important?
It probably relates to how positions of buoyant forces and center of gravity affect stability.
Absolutely! If the center of gravity and center of buoyancy are aligned, the object is stable. Remember, stability is crucial for ships!
The Concept of Metacenter
Unlock Audio Lesson
Now, let’s connect these concepts to the metacenter. What do you understand by metacenter?
Isn’t it the point that helps determine if a floating object is stable?
Right! The metacenter is crucial when an object tilts. When the center of buoyancy shifts, we can evaluate stability based on the relationship between the height of the metacenter and the center of gravity. Can anyone summarize the conditions for stable equilibrium?
If the metacenter is above the center of gravity, it’s stable!
Perfect! Remember the term ‘M-G contact’ where M is the metacenter and G is the center of gravity; that relationship defines stability.
Stability in Action
Unlock Audio Lesson
Let’s discuss real-life applications of buoyancy. Can anyone think of an example where stability is critically important?
What about boats? If they tilt too much, they could capsize!
Exactly! A boat's design keeps its metacenter above the center of gravity to prevent capsizing. What about swimmers?
They must balance to keep their center of buoyancy aligned to keep afloat!
Well said! Keep in mind the practical implications of stability and buoyancy in various aquatic situations.
Recap and Review
Unlock Audio Lesson
Let's summarize what we've learned about buoyancy, Archimedes' principle, and stability. Can some of you recap what Archimedes' principle states?
It states that the buoyant force on a submerged object is equal to the weight of the fluid displaced!
Correct! And how does this relate to the center of buoyancy?
The center of buoyancy is where that upward force acts.
Excellent! Lastly, what can you say about stability regarding the metacenter and the center of gravity?
If the metacenter is above the center of gravity, the object is stable.
Great job, everyone! This understanding is crucial for applications in fluid mechanics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into the principles of buoyancy as introduced by Archimedes, explaining how objects submerged in a fluid experience upward forces. It further discusses metacenters, stability of floating objects, and practical implications, such as the behavior of ships and swimmers in water.
Detailed
Detailed Summary of Buoyancy and Archimedes' Principle
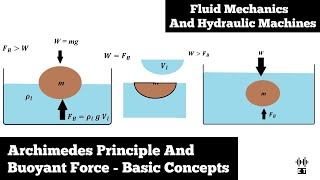
In this section, we analyze the foundational concepts of buoyancy and Archimedes' principle, which states that any submerged object experiences an upward force equal to the weight of the fluid displaced by the object. This force is known as buoyant force. The section elaborates on how this principle applies to various scenarios, particularly in fluid mechanics.
Key Points:
- Buoyancy Force: The upward force acting on an immersed object due to pressure differences.
- Center of Buoyancy: The center of mass of the fluid that has been displaced by an object submerged in it. The buoyant force acts through this point.
- Metacenter: Involved in analyzing the stability of floating bodies, the metacenter is defined as the point where an upright line through the center of buoyancy meets the centerline of the body when the body is tilted.
- Stability Concepts: The section explains three types of equilibrium—stable, unstable, and neutral—based on the relationships between the center of gravity and the metacenter (M). It emphasizes that a stable floating object will return to its original position after a disturbance.
The significance of these principles extends beyond academic theory; they are critical in designing floating structures like ships and understanding phenomena in various fields such as marine engineering and swimming.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Buoyancy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Buoyancy is a well-known phenomenon described by Archimedes' principle. When an object is submerged in a liquid, it experiences an upward buoyant force. This is due to the pressure differences above and below the object in the liquid.
Detailed Explanation
Buoyancy occurs when an object is placed in a fluid. The fluid exerts pressure on the object due to its weight, which creates a net upward force. The pressure at the bottom of the object is greater than the pressure at the top, leading to this upward force. This principle helps explain why objects feel lighter in water.
Examples & Analogies
Think about when you try to lift a heavy rock underwater versus lifting it in the air. Underwater, it feels much lighter because the buoyant force from the water is acting against the weight of the rock.
Archimedes' Principle
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
According to Archimedes' principle, a body submerged in a fluid experiences a buoyant force equal to the weight of the fluid it displaces. This principle can be summarized as: the buoyant force acting on a submerged object is equal to the weight of the fluid displaced by the object.
Detailed Explanation
Archimedes' principle states that the upward buoyant force on an object submerged in a fluid equals the weight of the liquid displaced by that object. For example, if a cube of a particular volume is submerged, it pushes aside a volume of fluid that weighs a specific amount; thus, the buoyant force equals that weight. This is essential when determining whether an object will float or sink.
Examples & Analogies
Consider a boat floating on a lake. The weight of the water displaced by the submerged part of the boat exactly equals the weight of the boat itself. If you add more weight to the boat (like more people getting in), it will displace more water until it either floats or starts to sink.
Center of Buoyancy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The center of buoyancy is the point through which the buoyant force acts. It is located at the centroid of the displaced fluid's volume and changes position as the object tilts or moves in the fluid.
Detailed Explanation
The center of buoyancy is crucial for understanding stability. As an object tilts in the water, the shape of the submerged volume changes, which can shift the position of the center of buoyancy. Knowing where this point is helps in predicting the stability of the floating object, as it relates to the center of gravity.
Examples & Analogies
Imagine a seesaw. If one side gets heavier, the seesaw tips to that side. Similarly, if a boat tilts, its center of buoyancy shifts, affecting how stable it is and whether it will tip over or right itself.
Stability of Floating Objects
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The stability of a floating object depends on the relationship between its center of gravity (CG) and its center of buoyancy (B). There are three types of equilibrium: stable, unstable, and neutral. A stable equilibrium returns to its original position after a disturbance, while an unstable equilibrium tips over.
Detailed Explanation
When a floating object is disturbed and tilts, the positions of its center of buoyancy and center of gravity come into play. If the center of buoyancy rises higher than the center of gravity when tilted, the object will return to its upright position, indicating stability. If the center of gravity is higher than the center of buoyancy, the object may capsize.
Examples & Analogies
Think of a tall tower. If it is perfectly straight and balanced, it's stable. However, if you push it slightly and it starts to lean, if it returns to its vertical position, it is stable. But if it starts to fall over, it represents unstable equilibrium.
The Metacenter
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The metacenter is a specific point used to determine the stability of floating bodies. It is defined as the intersection point of the vertical line through the center of buoyancy when displaced and the centerline of the floating object.
Detailed Explanation
The metacenter provides insight into the equilibrium of floating bodies. When an object tilts, the center of buoyancy shifts, and the metacenter is the point associated with the restoring moments that help the object right itself. By comparing the height of the metacenter to the center of gravity, one can classify the stability of the floating object.
Examples & Analogies
Visualize a boat on a lake. When waves push it to one side, the boat tilts but can return to an upright position; this restoration is influenced by the location of its metacenter. A high boat has a metacenter well above its center of gravity, giving it stability against tipping.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Buoyant Force: The upward force exerted on an object submerged in a fluid, equal to the weight of the fluid displaced.
-
Archimedes' Principle: A law stating that the buoyant force is equal to the weight of the fluid displaced by an object.
-
Center of Buoyancy: The centroid of the displaced fluid; point through which the buoyant force acts.
-
Metacenter: The point used to evaluate the stability of a floating object, determined by the position of the center of buoyancy when the object tilts.
-
Stability: The condition of equilibrium for floating objects; dependent on the relative positions of the metacenter and center of gravity.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A boat floating in water displaces a volume of water equal to its weight, demonstrating Archimedes' principle.
-
A swimmer adjusts their position in the water to maintain their balance, illustrating the concepts of center of buoyancy and stability.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In water boats float with grace, buoyancy keeps them in place.
📖 Fascinating Stories
-
Imagine a curious child dropping different objects into a pool. The stone sinks, while the wooden block floats. This mystery of floating and sinking is explained by Archimedes' principle and buoyancy.
🧠 Other Memory Gems
-
BFBP: Buoyant Force = Buoyant Property, where the property is weight of fluid displaced.
🎯 Super Acronyms
B.M.G.
- Buoyancy
- Metacenter
- Gravity
- emphasizing their relationships in stability.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Buoyancy
Definition:
The upward force exerted by a fluid that opposes the weight of an immersed object.
-
Term: Archimedes' Principle
Definition:
A principle stating that an object submerged in a fluid experiences an upward force equal to the weight of the fluid it displaces.
-
Term: Center of Buoyancy
Definition:
The point within a submerged object where the buoyant force acts, located at the centroid of the displaced fluid.
-
Term: Metacenter
Definition:
The point where the buoyant force acts when a floating body is tilted, essential for determining stability.
-
Term: Stability
Definition:
The ability of a floating object to return to its original position after a disturbance; defined by the relationship between metacenter and center of gravity.