Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Buoyancy
Unlock Audio Lesson
Today, we're starting with buoyancy, the principle first described by Archimedes. Can anyone tell me what buoyancy is?
It's the upward force that a fluid exerts on an object submerged in it.
Exactly! The buoyant force is equal to the weight of the fluid displaced by the object. This is crucial for floating. Can anyone give me an example of how this applies in real life?
Like a boat floating on water?
Right! And remember the acronym 'D.O.W.'—Displacement of Water explains how buoyancy works. Let's shift to the concept of the center of buoyancy.
What is the center of buoyancy?
Great question! The center of buoyancy is the centroid of the displaced fluid volume. It affects stability when the object tilts.
So, if the center of buoyancy shifts, it could change the stability of the object?
Exactly! Let's summarize: buoyancy helps objects float when they displace enough fluid their weight, and the center of buoyancy is key to stability.
Metacenter and Stability
Unlock Audio Lesson
Now, let’s talk about the metacenter. When a floating body tilts, how do we determine if it's stable or not?
Is that where the buoyant force acts?
Yes! The metacenter is the intersection of the buoyancy line and the vertical through the center of gravity. It helps determine stability.
What happens if the metacenter is above the center of gravity?
That indicates stable equilibrium. The object will return to its original position after a slight tilt. Remember the acronym 'M.G.H.'—Metacenter is Greater than Height for stability.
And what if the metacenter is below the center of gravity?
That's unstable equilibrium; small disturbances could capsize the object. Can anyone think of a real-world example?
Maybe large ships in stormy weather?
Exactly! So in summary, the position of the metacenter relative to the center of gravity is pivotal in understanding a floating object’s stability.
Calculating Metacentric Height
Unlock Audio Lesson
Next, let’s calculate the metacentric height. Does anyone know how to approach this calculation?
We can use the area of the submerged part of the object?
Great! We look at the volume submerged and the moment of inertia about the axis. What’s the formula we can use?
Is it MG = I/V?
Close! MG relates to the metacentric height, buoyancy, and submerged volume. This can give us an idea of stability.
How do we interpret MG values?
If MG is positive, we have stable equilibrium; zero means neutral; and negatives indicate instability. Let’s summarize: the formula gives insights into the stability of floating structures.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore Archimedes' principle of buoyancy, the calculations for finding the metacentric height, and how these concepts are crucial for ensuring the stability of floating objects. We delve into the relationships between the center of gravity and buoyancy, and the types of equilibrium that affect stability.
Detailed
Metacenter and Stability Calculation
This section focuses on the principles of buoyancy and stability in fluid mechanics, particularly for floating objects. It begins with an overview of Archimedes' principle, which states that any object submerged in a fluid experiences a buoyant force equal to the weight of the fluid displaced by the object. This principle is fundamental in understanding how objects float.
Key Concepts Covered:
- Buoyancy: The upward force that acts on a submerged object. The buoyant force equals the weight of the fluid displaced.
- Center of Buoyancy: The centroid of the displaced fluid volume, where the buoyant force is considered to act.
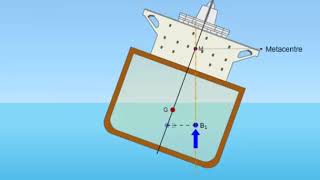
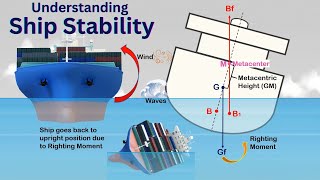
- Metacentric Height (GM): This is a critical measurement in understanding the stability of floating bodies. The metacenter is the point where the buoyant force acts when an object is tilted.
Types of Equilibrium:
- Stable Equilibrium: Occurs when the metacenter (M) is above the center of gravity (G). A small tilt will restore the object to its original position.
- Unstable Equilibrium: Occurs when M is below G. A small tilt will cause the object to capsize.
- Neutral Equilibrium: Occurs when M coincides with G, resulting in no restoring moment.
The section concludes with methods to calculate the metacentric height and the implications for the design of ships and floating structures. Understanding these concepts is crucial for engineers working with maritime vessels.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Buoyancy and Metacenter
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us come it to very interesting topics what is we use in buoyancy as you know it the famous scientist Archimedes what invented this buoyancy concept when he was in a bathtub experienced the lighter weight because of the buoyancy forces. So what is the buoyancy force if you look it that, it is a very simple things that whenever you have any object, okay submerged within a liquid, what will happen it that there will be a force from the top also force from the bottom.
Detailed Explanation
Buoyancy is a force that acts on an object immersed in a fluid, which in this case is water or liquid. The principle behind buoyancy was discovered by Archimedes, who realized that objects submerged in a fluid experience an upward force, which is equal to the weight of the fluid that they displace. For any object submerged under water, there is pressure acting on both the top and bottom surfaces of the object. The pressure exerted by the liquid increases with depth, meaning the pressure at the bottom of the object is greater than the pressure at the top. This difference in pressure results in a net upward force, known as the buoyant force, acting on the object.
Examples & Analogies
One way to visualize this is to think of a beach ball partially submerged in water. The ball experiences an upward buoyant force from the water below it that helps keep it afloat, while the weight of the ball tries to pull it down. This scenario is similar to how ships float on water; they displace enough water to create an upward force strong enough to balance their weight.
Center of Buoyancy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look it another point is we also look it that the center of buoyancy. That means the line of actions of the buoyant force like we try to compute for the other force component. So line of actions of the buoyant force is the center of buoyancy.
Detailed Explanation
The center of buoyancy is the point through which the buoyant force acts. It is the centroid of the submerged volume of the object. When an object is floating, the weight of the object acts downward through its center of gravity (CG), while the buoyant force acts upward through the center of buoyancy. The position of these two points—CG and the center of buoyancy—is crucial when analyzing the stability of the floating object. For the object to be stable, these forces must be well aligned, and the center of buoyancy typically lies below the center of gravity when the object is stable.
Examples & Analogies
Consider a seesaw. For it to balance properly, the weights (or forces) must be aligned over the pivot point. If one side is heavier, it tips. Similarly, if the CG of an object is higher than its center of buoyancy, the object is prone to tipping over, just like how the seesaw tilts when one side is heavier.
Equilibrium Concepts
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us understand the principles the how the concept is conceived. As we discussed that there will be a gravity force which will act the CG of the floating object and there will be the force which is a buoyant force will act as the CG of the displaced liquid that what will be the center of buoyancy. So these two force components act at two different location.
Detailed Explanation
In fluid mechanics, we analyze the stability of floating objects based on three types of equilibrium: stable equilibrium, unstable equilibrium, and neutral equilibrium. When an object is in stable equilibrium, it tends to return to its original position after a small disturbance, such as tilting. Conversely, if it tips over and continues to tilt, it is in unstable equilibrium. Neutral equilibrium occurs when an object remains in its new position after being tilted without returning to the original position. The balance between the buoyant force acting at the center of buoyancy and the weight acting at the center of gravity determines the type of equilibrium.
Examples & Analogies
Think of a pencil balanced on a finger. If the pencil is perfectly vertical, it is in stable equilibrium; if you slightly move it, it returns upright. If you balance the pencil horizontally on your finger, even the slightest movement will cause it to fall, exemplifying unstable equilibrium. When a toddler sits down on a seesaw, the equilibrium might change based on their weight distribution. Therefore, depending on how forces are aligned, different types of equilibrium can be observed.
Metacenter Definition and Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Before doing that, let me introduce one point, which is we call the metacenters, okay. That is what is called the metacenter. What is that metacenters, okay? If I tilt it, a floating object to a angle of delta theta, then there will be a new waterlines will come it.
Detailed Explanation
The metacenter is a point that helps determine the stability of a floating object when it is tilted. When the object tilts, its center of buoyancy shifts to a new location, and the line of action of the buoyant force also changes. The metacenter is defined as the point where the upward buoyant force acts when a vessel is tilted at a small angle. If the metacenter is above the center of gravity, the object will be stable; if it is below, the object will be unstable. We can calculate the metacentric height by evaluating areas related to the object's geometry and the submerged volume displacement.
Examples & Analogies
Picture a rowboat. When a person sits upright, their weight is balanced by the buoyant force. If they lean over the edge, the boat may tilt, causing the center of buoyancy to rise. If the weight of the person is above the metacenter, the boat will return to upright; if below, the boat may tip over. This is similar to how tall buildings need a strong foundation—if the height is not balanced by the base's weight, the structure could topple.
Conclusion on Stability
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now how to compute this the metacentric height? Let you have a floating object like this, okay? And you consider the unit width of this ones which is a perpendicular to this surface that is what unit width is there.
Detailed Explanation
To calculate the metacentric height of a floating object, we consider the geometry of the submerged part of the object and the distribution of forces. The metacentric height can be determined using specific equations that relate the moments of the submerged volume to the gravitational forces acting on the object. With the metacentric height known, we can assess if the object is in stable equilibrium. If the calculations yield a positive height, it indicates stability; if zero, it indicates neutral equilibrium, and if negative, unstable equilibrium.
Examples & Analogies
Consider how engineers design ships. They will meticulously calculate the metacentric height to ensure the design keeps the ship upright and stable in water, especially as conditions change—like waves or cargo shifts. The same principle is applied to design amusement park rides to ensure safety, keeping them from tipping or rolling over during operation.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Buoyancy: The upward force that acts on a submerged object. The buoyant force equals the weight of the fluid displaced.
-
Center of Buoyancy: The centroid of the displaced fluid volume, where the buoyant force is considered to act.
-
Metacentric Height (GM): This is a critical measurement in understanding the stability of floating bodies. The metacenter is the point where the buoyant force acts when an object is tilted.
-
Types of Equilibrium:
-
Stable Equilibrium: Occurs when the metacenter (M) is above the center of gravity (G). A small tilt will restore the object to its original position.
-
Unstable Equilibrium: Occurs when M is below G. A small tilt will cause the object to capsize.
-
Neutral Equilibrium: Occurs when M coincides with G, resulting in no restoring moment.
-
The section concludes with methods to calculate the metacentric height and the implications for the design of ships and floating structures. Understanding these concepts is crucial for engineers working with maritime vessels.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of buoyancy is a boat floating on water, where the weight of the water displaced is equal to the weight of the boat.
-
A submerged block of wood displaces water, creating a buoyant force that is equal to the weight of the wood block.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When things float, they find their way, the fluid lifts them every day.
📖 Fascinating Stories
-
Imagine a tiny boat on a calm lake. It floats easily because it pushes water away, just like people in water can feel light due to buoyancy, thanks to Archimedes.
🧠 Other Memory Gems
-
B & H: Buoyant forces Help understand why things float!
🎯 Super Acronyms
M.G.G.
- Metacenter is Greater than Gravity for stability!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Buoyancy
Definition:
The upward force exerted by a fluid on an object placed in it.
-
Term: Center of Buoyancy
Definition:
The centroid of the fluid volume displaced by a submerged object, where the buoyant force acts.
-
Term: Metacenter
Definition:
The point at which the buoyant force acts when an object is tilted.
-
Term: Metacentric Height (GM)
Definition:
The distance between the center of gravity and the metacenter, affecting the stability of floating objects.
-
Term: Equilibrium
Definition:
A state in which opposing forces or influences are balanced.