Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Buoyancy
Unlock Audio Lesson
Let's start by discussing what buoyancy is. Can anyone tell me what happens when an object is submerged in water?
I think it experiences an upward force!
Exactly! This upward force is what we call the buoyant force, and it always equals the weight of the fluid that the object displaces, according to Archimedes' principle.
So, if an object displaces more water, does it experience a greater buoyant force?
Great question! Yes, the more water it displaces, the greater the buoyant force it experiences. Remember, it's not about the weight of the object itself, but the weight of the fluid displaced.
Is this the reason why some objects float while others sink?
Exactly! If the weight of the object is less than the buoyant force, it will float. It's all about the relationship between weight and buoyancy.
Center of Buoyancy
Unlock Audio Lesson
Now let's discuss the center of buoyancy. What do you think it represents?
Is it the point where the buoyant force acts?
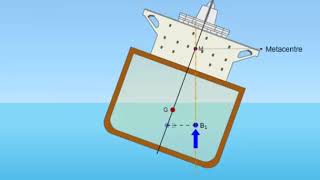
Correct! The center of buoyancy is the centroid of the displaced volume of fluid. It serves as the point through which the buoyant force acts. Can anyone explain how this relates to an object's center of gravity?
I think it's important because both points need to align for stability.
Exactly! If the center of buoyancy is above the center of gravity, the object is more likely to be stable.
What happens if they're not aligned?
Great question! If the center of gravity is above the center of buoyancy, the object can become unstable and capsize.
Equilibrium and Stability
Unlock Audio Lesson
Let's dive into equilibrium types. Can anyone name the three types of equilibrium we discuss in fluid mechanics?
Stable, unstable, and neutral equilibrium!
Exactly! Stable equilibrium occurs when the metacenter is above the center of gravity (M > G), leading to restoring moments. What about the other cases?
If the metacenter is below the center of gravity, that's unstable equilibrium. It would tipping over, right?
That's right! In unstable equilibrium, a tilt can lead to capsizing. Neutral equilibrium is when M equals G, meaning the object can remain tilted without returning to an original position. Can you think of examples for these?
A cork floating on water would be stable, but a very tall and narrow object might be unstable!
Excellent examples! Understanding these concepts is crucial in designing ships and floating devices.
Calculating Stability and Metacentric Height
Unlock Audio Lesson
Finally, let’s talk about calculating metacentric height. Why do you think it’s important?
It helps us determine how stable a floating object is!
That's correct! The metacentric height gives us insight into the stability of the floating object. Can anyone explain how we calculate it?
I think we look at the moments around the center of buoyancy, right?
Exactly! We use the relationship between the displaced volume and the moment of inertia to find the metacentric height. This calculation allows engineers to design stable vessels.
What if the conditions change, like the weight of the cargo?
That's a key consideration! Any change in weight affects the center of gravity, which in turn affects the stability. This is why continuous assessment in ship design and operation is critical.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The concept of buoyancy is explored, emphasizing Archimedes' principle and the center of buoyancy. The section also details the stability of floating objects and the role of metacenters in determining stability.
Detailed
Center of Buoyancy
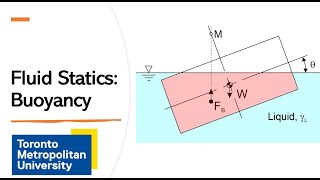
Buoyancy is defined as the upward force exerted by a fluid on a submerged object, which is equal to the weight of the fluid displaced. This section elaborates on the concept introduced by Archimedes, explaining that when an object is submerged in a liquid, it experiences pressure from both the top and bottom, creating a net upward force due to the liquid displaced.
Key factors in understanding buoyancy include the centers of gravity and buoyancy. The center of buoyancy is the centroid of the displaced fluid volume and plays a crucial role in maintaining the equilibrium of floating bodies.
Stability is an essential aspect to consider in buoyancy scenarios. A floating object is stable if it returns to its original position after a disturbance. This stability relies on the relative positions of the center of gravity (CG) and the metacenter. The latter is critical in determining whether a floating object will right itself after being tilted. This section articulates the conditions for stable, unstable, and neutral equilibrium, explaining that:
- Stable equilibrium occurs when the metacenter is above the center of gravity (M > G), resulting in restoring moments.
- Unstable equilibrium occurs when the center of gravity is above the metacenter (M < G), leading to a tendency to capsize.
The methods for calculating the metacentric height required for stability in various scenarios are also discussed, alongside numerical examples. Understanding the principle of buoyancy and its relationship with stability is foundational in fields such as naval architecture and fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of Buoyant Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Whenever you have any object submerged within a liquid, there will be a force from the top due to the liquid mass and a force from the bottom in an upward direction. The buoyant force is equivalent to the weight of the liquid displaced by that object.
Detailed Explanation
The buoyant force acts on submerged objects and is the result of differences in pressure within the fluid. The pressure at the bottom of the object is greater than that at the top due to the weight of the fluid above it. By considering a control volume around the submerged object, we can calculate the upward buoyant force as equal to the weight of the liquid displaced, which is the fluid's density multiplied by the volume of the submerged part of the object.
Examples & Analogies
Think of a balloon submerged underwater. When you let go, it floats back up to the surface, which illustrates the buoyant force at play. The water pushes up on the balloon with a force equal to the weight of the water the balloon displaces.
Center of Buoyancy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The center of buoyancy is the point where the buoyant force acts and is effectively the centroid of the displaced fluid volume. This means it is the average location of the buoyant force that counteracts the weight of the floating object.
Detailed Explanation
The center of buoyancy is critical for understanding stability in floating systems. It is located at the centroid of the fluid displaced by an object and affects how the object responds to tilting. For example, when a swimmer is in water, their center of gravity and center of buoyancy are located at different points, leading to torque that the swimmer must counteract to stay afloat.
Examples & Analogies
Imagine a seesaw. If the weight is balanced at the center, it stays level. If one side is heavier and moves down, it causes the seesaw to tilt. Similarly, the center of buoyancy acts like the balance point in situations where the forces of buoyancy and gravity interact.
Archimedes’ Principle
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Archimedes’ principle states that a body immersed in a fluid experiences a vertical buoyant force equal to the weight of the fluid displaced by that body. This force acts upward through the centroid of the displaced volume.
Detailed Explanation
Archimedes' principle establishes that the buoyant force acting on a submerged object contributes to its overall stability. When a solid object is fully or partially submerged, it displaces a volume of fluid, and an upward force equal to the weight of this displaced fluid acts on the object, allowing it to float or sink.
Examples & Analogies
Consider an ice cube floating in a glass of water. The weight of the water displaced by the submerged part of the ice cube equals the weight of the ice cube itself. When the water levels out, we see that part of the ice is above the surface due to the balance of forces, illustrating Archimedes' principle.
Stability of Floating Objects
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The stability of floating objects depends on the positions of the center of gravity (CG) and the center of buoyancy (CB). If the center of buoyancy is above the center of gravity, the object will return to its upright position when tilted.
Detailed Explanation
For an object to remain stable while floating, the center of buoyancy must be higher than the center of gravity. When the object is tilted, the center of buoyancy shifts. If during that shift, the vertical line of the buoyancy force aligns better with the center of gravity, a restoring moment is generated that helps the object return to its initial position. Conversely, if the center of buoyancy is below the center of gravity, the object will be unstable and may capsize.
Examples & Analogies
Think of a boat on water. When someone shifts their weight to one side of the boat, the center of gravity moves. If the boat can return to an upright position after the person shifts, it is stable. If the boat capsizes instead, it shows the importance of having a properly positioned center of gravity and buoyancy.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Buoyant Force: The upward force acting on a submerged object due to fluid displacement.
-
Center of Buoyancy: The point where the buoyant force acts, located at the centroid of the displaced fluid.
-
Metacenter: An important point to determine stability, where the buoyant line intersects.
-
Stable Equilibrium: Occurs when the floating object returns to its original position after a disturbance.
-
Unstable Equilibrium: When a slight disturbance leads to capsizing.
-
Neutral Equilibrium: When an object remains in its new position after disturbance.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A ship floating in water experiences an upward buoyant force equal to the weight of the water displaced.
-
When a cork is placed in water, it floats because the buoyant force is greater than its weight.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Buoyancy soars like a bird in air, Upward force gives everything care.
📖 Fascinating Stories
-
Imagine a boat on a calm lake. It floats peacefully, just like how you feel when you have support beneath; that support is buoyancy, lifting you safely.
🧠 Other Memory Gems
-
Remember: B for Buoyancy, U for Upward, O for Object, and A for Archimedes. It’s a strong connection!
🎯 Super Acronyms
B.O.A.T. - Buoyant Objects Are Tool-tested in water.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Buoyant Force
Definition:
The upward force exerted by a fluid on a submerged object, equal to the weight of the fluid displaced.
-
Term: Center of Buoyancy
Definition:
The centroid of the displaced volume of fluid, which is the point through which the buoyant force acts.
-
Term: Metacenter
Definition:
The point at which the vertical line through the center of buoyancy intersects with the vertical line through the center of gravity of a floating body.
-
Term: Stable Equilibrium
Definition:
Condition where a floating object returns to its original position after being disturbed (M > G).
-
Term: Unstable Equilibrium
Definition:
Condition where a floating object tends to capsize if disturbed (M < G).
-
Term: Neutral Equilibrium
Definition:
Condition where a floating object remains in its altered position after being tilted (M = G).