Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Buoyancy
Unlock Audio Lesson
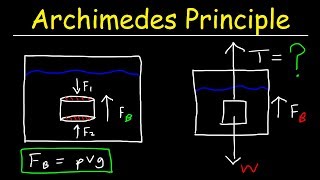
Today, we will delve into the fascinating world of buoyancy. Can anyone tell me about Archimedes' principle?
Isn't it the idea that a body submerged in fluid experiences an upward force equal to the weight of the fluid displaced?
Absolutely right! This upward force is known as the buoyant force. Remember, buoyancy is key in many applications, such as ships floating on water. You can think of the mnemonic 'Buoyancy = Up' to remember its direction.
What does it mean for an object to be in equilibrium when talking about buoyancy?
Great question! Equilibrium in this context refers to the balance between forces acting on an object. We have stable, unstable, and neutral equilibrium. Let’s dive deeper into that!
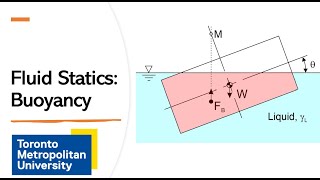
Center of Buoyancy and its Role
Unlock Audio Lesson
The center of buoyancy is crucial; it’s the point where the buoyant force is considered to act. Why do you think this is important?
Because it helps determine how stable an object is while floating!
Exactly! The location of the center of buoyancy affects stability, especially concerning the center of gravity. A memory aid to keep in mind is 'B below G for stability'.
What happens when the CG and CB are not aligned?
Good observation! If the CG is above the CB, the object might tip over, leading to an unstable equilibrium. Conversely, if the CB is above the CG, the object is likely to return to its upright position.
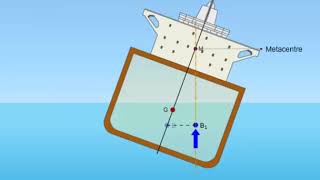
Metacenter and Stability
Unlock Audio Lesson
Let’s discuss the metacenter, a vital point for understanding floating stability. Who can summarize what the metacenter is?
Isn't it the point where the vertical line through the center of buoyancy intersects the centerline of an object?
Correct! The distance to the center of gravity from the metacenter helps us find stability mathematically. We can use ‘BM > BG for stability’. That means if BM is greater than BG, the object is stable.
How do we determine the metacentric height?
It involves calculating the volume of the displaced fluid and its moment. If we understand how to calculate both, we can assess how stable an object will be!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the fundamental concepts of buoyancy introduced by Archimedes, including how buoyant forces act on submerged objects, the calculation of metacentric height, and the different equilibrium states affecting the stability of floating bodies, emphasizing real-life applications in engineering and physics.
Detailed
Detailed Summary of Buoyant Forces and Stability
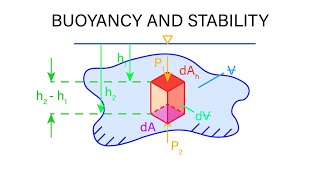
In fluid mechanics, buoyancy refers to the upward force exerted by a fluid on a submerged object, made famous by Archimedes' principle. This principle states that a body submerged in a fluid experiences a buoyant force equal to the weight of the fluid it displaces. Central to buoyancy is the concept of the center of buoyancy, which is the center of mass of the displaced fluid.
For floating objects, stability is determined by the relationship between the center of gravity (CG) of the object and the center of buoyancy (CB). The section elaborates on three types of equilibrium—natural, stable, and unstable. A stable equilibrium occurs when a slight tilting of the object leads to a restoring moment that brings the object back to its original position. The metacentric height is a crucial parameter in determining stability; it is the distance from the center of gravity to the metacenter, where the buoyant force can be considered to act during tilting. Understanding these concepts is vital for applications such as ship design and stability assessments in engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Buoyancy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Archimedes' principle states that a body immersed in a fluid experiences a vertical buoyant force which is equal to the weight of the fluid displaced by that body.
Detailed Explanation
Buoyancy is essentially the force that pushes an object upwards when it is submerged in a fluid. According to Archimedes' principle, the upward force (buoyant force) acting on the submerged object is equivalent to the weight of the fluid that the object displaces. This principle helps us to understand why some objects float while others sink.
Examples & Analogies
Think of a balloon filled with air submerged in water. The balloon floats because the water it displaces weighs more than the balloon itself. If the balloon were filled with a liquid that weighed more than the water, it would sink. This is similar to how a ship floats on water; it displaces a large volume of water resulting in enough buoyant force to keep it afloat.
Center of Buoyancy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The center of buoyancy is the centroid of the volume of fluid displaced by a submerged object, and it acts as the point through which buoyant force can be considered to act.
Detailed Explanation
The center of buoyancy is crucial for understanding stability in floating objects. It is the point where the buoyant force effectively acts and is calculated as the average location of the displaced fluid. If the center of buoyancy is above the center of gravity (the point where the weight of the object acts), the object is likely to be stable when tilted.
Examples & Analogies
Imagine a person floating on their back in a pool. The buoyant forces from the water act on the center of the part of the water they displace, which is the center of buoyancy. If they lean to one side, the center of buoyancy shifts, making it easier for them to return to a flat position on the water surface, just like how a boat right itself when tilted.
Equilibrium in Floating Objects
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The stability of a floating object is determined by the relationship between the center of gravity and the center of buoyancy. This can result in natural, stable, or unstable equilibrium.
Detailed Explanation
Equilibrium refers to the balance point of a floating object. When the center of buoyancy (B) is above the center of gravity (G), the object is in a stable equilibrium, meaning it will return to its original position after a disturbance. If B is below G, the object is in an unstable equilibrium and will topple over. Natural equilibrium occurs when they are at the same point, maintaining the object's position no matter how it is tilted.
Examples & Analogies
Consider a toy boat in a bathtub. If you tilt the boat slightly, if it has a stable equilibrium, it will return to an upright position due to the force of the displaced water acting at a higher point. Conversely, if you placed a large weight at the top of the boat, it might tip over easily, illustrating unstable equilibrium.
Metacentric Height
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The metacentric height (GM) is the distance between the center of gravity (G) and the metacenter (M), which reflects the stability of the floating object.
Detailed Explanation
The metacenter is a point where the buoyant force acts when a floating body is tilted. The distance from the center of gravity to the metacenter (GM) indicates stability: a larger distance means greater stability. When a floating body is tilted, the center of buoyancy shifts, and if the metacenter is above the center of gravity, a restoring torque acts to return the body to its upright position.
Examples & Analogies
Think about a tall, thin boat compared to a wide, flat barge. The tall boat, if tilted, has a smaller GM because its metacenter is closer to its center of gravity, making it less stable. In contrast, the wide barge, with a larger GM, can tilt significantly before capsizing, thanks to its design which gives it a bigger restoring force to right itself.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Buoyant Force: The upward force acting on a submerged object that opposes its weight.
-
Archimedes' Principle: States that the buoyant force is equal to the weight of the fluid displaced by the object.
-
Metacenter: The point at which the line of action of buoyancy intersects the vertical centerline when the object is tilted.
-
Stability: The capacity of an object to return to its original position after being disturbed.
-
Equilibrium States: The conditions under which an object's forces are balanced; these can be natural, stable, or unstable.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A ship floating on water displaces an amount of water equal to its weight, demonstrating buoyant force.
-
A swimmer adjusts their body position to maintain balance in the water, illustrating stability and center of buoyancy concepts.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Buoyant forces rise, keep objects afloat, Down in the fluid, they like to gloat.
📖 Fascinating Stories
-
Once Archimedes stepped into a tub, he noticed the water spilling over. This led him to deduce that every submerged object pushes water equal to its weight, sparking the discovery of buoyancy!
🧠 Other Memory Gems
-
BUBBLE - Buoyant Upward Body Balance Forces Lift Everywhere.
🎯 Super Acronyms
MGB - Metacenter Greater than Gravity for stability.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Buoyant Force
Definition:
The upward force exerted by a fluid on a submerged object, equal to the weight of the fluid displaced by the object.
-
Term: Center of Buoyancy
Definition:
The centroid of the displaced volume of fluid, where the buoyant force is considered to act.
-
Term: Metacentric Height
Definition:
The distance between the center of gravity (CG) of a floating body and its metacenter (M).
-
Term: Equilibrium
Definition:
A state in which all the forces acting on an object are balanced.
-
Term: Stable Equilibrium
Definition:
A state where an object returns to its original position after a slight disturbance.
-
Term: Unstable Equilibrium
Definition:
A state where a slight disturbance causes the object to tip over or move further from its original position.